应用举例:餐饮企业菜品搭配; 搜索引擎内容的推荐;新闻流行趋势的分析。
| TID | ITEMS |
| 001 | Cola, Egg, Ham |
| 002 | Cola, Diaper, Beer |
| 003 | Cola, Diaper, Beer, Ham |
| 004 | Diaper, Beer |
事务:一条数据; 项:Egg 一项; 项集 {Egg, Ham} 2-项集
关联规则(association rule): {a} -> {b}。{a}叫做前件,{b}叫做后件。
支持度计数:商品总和出现的次数。{Diaper, Beer}出现在事务 002、003和004中,所以它的支持度计数是3
支持度(support):支持度计数/总的事务数。{Diaper, Beer}的支持度计数为3,所以它的支持度是3/4=75%,说明有75%的人同时买了Diaper和Beer。主要作用是删去无意义的规则。
置信度(confidence):对于规则{Diaper}→{Beer},{Diaper, Beer}的支持度计数/{Diaper}的支持度计数,为这个规则的置信度。例如规则{Diaper}→{Beer}的置信度为3÷3=100%。说明买了Diaper的人100%也买了Beer。置信度衡量推出的规则的可靠性。
提升度:商品A的出现对商品B的出现概率提升的程度。
提升度(A->B) = 置信度(A->B)/支持度(B)
提升度(A->B) > 1:代表有提升
提升度(A->B) = 1:代表没有提升也没有下降
提升度(A->B) < 1:代表有下降
频繁项集(frequent itemset):支持度大于或等于某个阈值的项集就叫做频繁项集。例如阈值设为50%时,因为{Diaper, Beer}的支持度是75%,所以它是频繁项集。
强关联规则(strong rule)发现指的是找出支持度>=最小支持度阈值(minsup)并且置信度>=最小置信度阈值(minconf)的所有规则。
项集的超集:包含这个项集的元素且元素个数更多的项集。
A => B
Support = freq(A,B)/N
Confidence = freq(A,B)/freq(A)
Lift = Support / ( Support(A)* Support(B) )
| T1 | A | B | C |
| T2 | A | C | D |
| T3 | B | C | D |
| T4 | A | D | E |
| T5 | B | C | E |
| Rule | Support | Confidence | Lift |
| A => D | 2/5 | 2/3 | 2/5 / (3/5 * 3/5) = 10/9 |
| C => A | 2/5 | 2/4 | 2/5 (4/5 * 3/5) = 5/6 |
| A => C | 2/5 | 2/3 | 2/5 (3/5 * 4/5) = 5/6 |
| B, C => A | 1/5 | 1/3 | 1/5 (3/5 * 3/5) = 5/9 |
Apriori算法
如果一个集合是频繁项集,则它的所有子集都是频繁项集。
如果一个集合不是频繁项集,则它的所有超集都不是频繁项集。
Apriori算法是发现频繁项集的一种方法。步骤是连接+剪纸。
Apriori算法的两个输入参数分别是最小支持度和数据集。该算法首先会生成所有单个元素的项集列表。接着扫描数据集来查看哪些项集满足最小支持度要求,那些不满足最小支持度的集合会被去掉。然后,对剩下来的集合进行组合以生成包含两个元素的项集。接下来,再重新扫描交易记录,去掉不满足最小支持度的项集。该过程重复进行直到所有项集都被去掉。
该算法需要不断寻找候选集,然后剪枝即去掉非频繁子集的候选集,时间复杂度由暴力枚举所有子集的指数级别O(n^2)降为多项式级别,多项式具体系数是底层实现情况而定的。
另外,阈值设置的越小,整体算法的运行时间就越短,因为阈值设置的越小,剪纸会更早介入。
| 订单编号 | 购买的商品 |
| 1 | 1,2,3 |
| 2 | 4,2,3,5 |
| 3 | 1,3,5,6 |
| 4 | 2,1,3,5 |
| 5 | 2,1,3,4 |
1.先计算单个商品的支持度,也就是得到k=1项的支持度 (假定最小支持度是0.5)
| 商品项集 | 支持度 |
| 1 | 4/5 |
| 2 | 4/5 |
| 3 | 5/5 |
| 4 | 2/5 |
| 5 | 3/5 |
| 6 | 1/5 |
| 商品项集 | 支持度 |
| 1 | 4/5 |
| 2 | 4/5 |
| 3 | 5/5 |
| 5 | 3/5 |
2.在这个基础上,将商品两两组合,得到k=2项的支持度
| 商品项集 | 支持度 |
| 1,2 | 3/5 |
| 1,3 | 4/5 |
| 1,5 | 2/5 |
| 2,3 | 4/5 |
| 2,5 | 2/5 |
| 3,5 | 3/5 |
| 商品项集 | 支持度 |
| 1,2 | 3/5 |
| 1,3 | 4/5 |
| 2,3 | 4/5 |
| 3,5 | 3/5 |
3.再将商品进行k=3项的商品组合
| 商品项集 | 支持度 |
| 1,2,3 | 3/5 |
| 1,3,5 | 2/5 |
| 2,3,5 | 2/5 |
| 商品项集合 | 支持度 |
| 1,2,3 | 3/5 |
FP-Growth 算法
FP-Growth不产生候选集。
FP-Growth只需扫描2次数据集。
数据集映射到一颗FP(Frequent Pattern 频繁模式)树上,再从这棵树挖掘频繁项集。
创建一颗FP树来存储频繁项集,在创建前对不满足最小支持度的项进行删除,减少了存储空间。
步骤:
1.首先对事务中的每个项计算支持度,丢弃其中非频繁的项,每个项的支持度进行倒序排序。同时对每一条事务中的项也按照倒序进行排序。
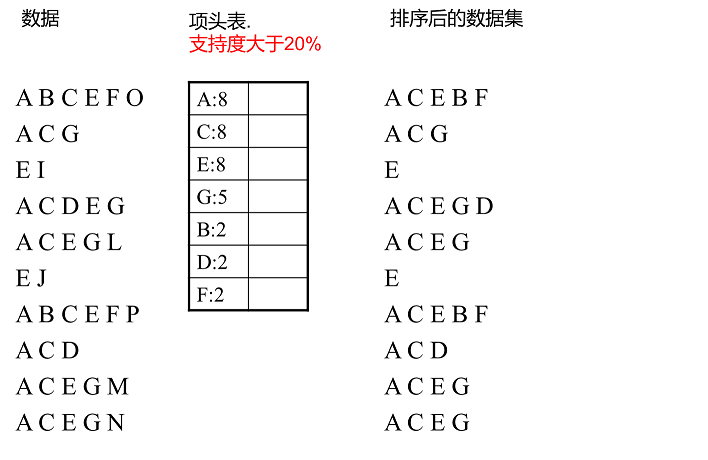
2.根据每条事务中事务项的新顺序,依此插入到一棵以Null为根节点的树中。同时记录下每个事务项的支持度。这个过程完成之后,我们就得到了棵FP-tree树结构。
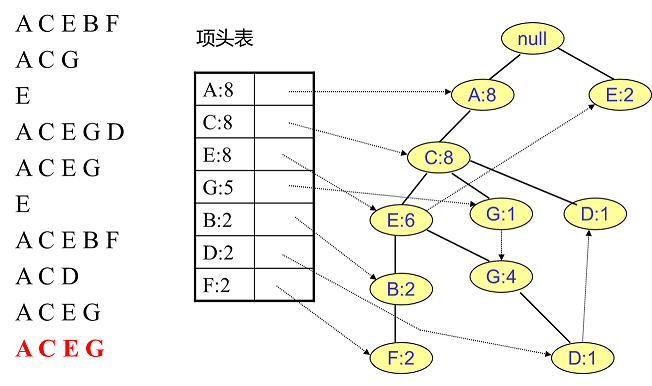
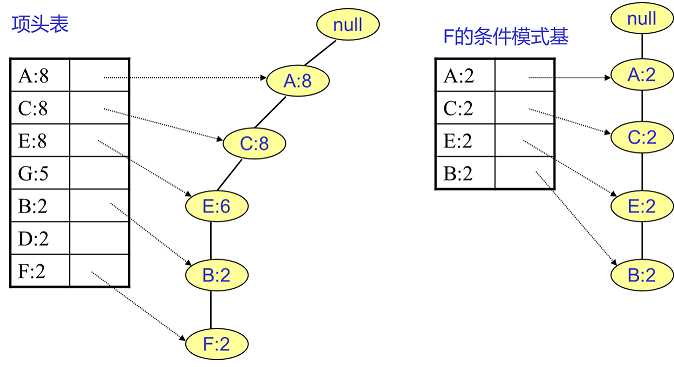
3.从FP-tree中获得条件模式基,利用条件模式基,构建一个FP子树,重复迭代,找出所有频繁项集。条件模式基:相对于树中某个元素来说,指该元素在树中的前缀路径,是介于该元素与树根节点之间的所有内容。
F的频繁2项集为{A:2,F:2}, {C:2,F:2}, {E:2,F:2}, {B:2,F:2}。递归合并二项集,得到频繁三项集为{A:2,C:2,F:2},{A:2,E:2,F:2},...还有一些频繁三项集,就不写了。当然一直递归下去,最大的频繁项集为频繁5项集,为{A:2,C:2,E:2,B:2,F:2}。
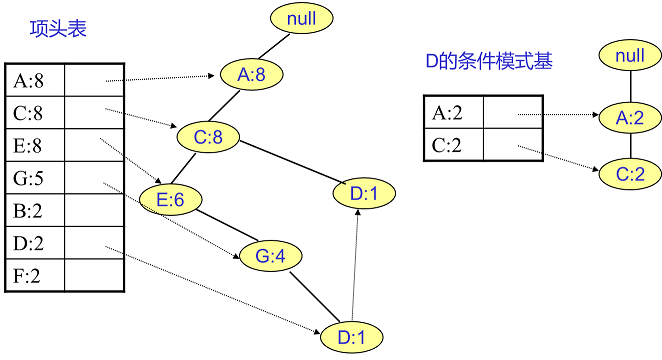
D节点比F节点复杂一些,因为它有两个叶子节点,因此首先得到的FP子树如下图左。我们接着将所有的祖先节点计数设置为叶子节点的计数,即变成{A:2, C:2,E:1 G:1,D:1, D:1}此时E节点和G节点由于在条件模式基里面的支持度低于阈值,被我们删除,最终在去除低支持度节点并不包括叶子节点后D的条件模式基为{A:2, C:2}。通过它,我们很容易得到D的频繁2项集为{A:2,D:2}, {C:2,D:2}。递归合并二项集,得到频繁三项集为{A:2,C:2,D:2}。D对应的最大的频繁项集为频繁3项集。
同样的方法可以得到B的条件模式基如下图右边,递归挖掘到B的最大频繁项集为频繁4项集{A:2, C:2, E:2,B:2}。
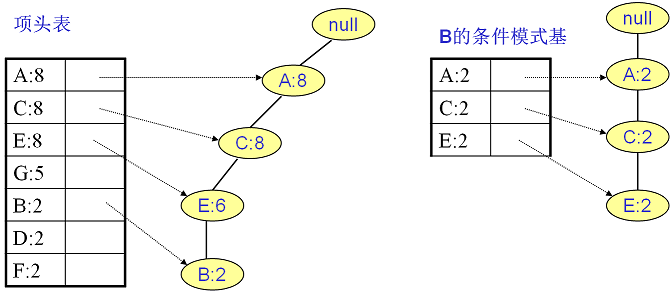
继续挖掘G的频繁项集,挖掘到的G的条件模式基如下图右边,递归挖掘到G的最大频繁项集为频繁4项集{A:5, C:5, E:4,G:4}。
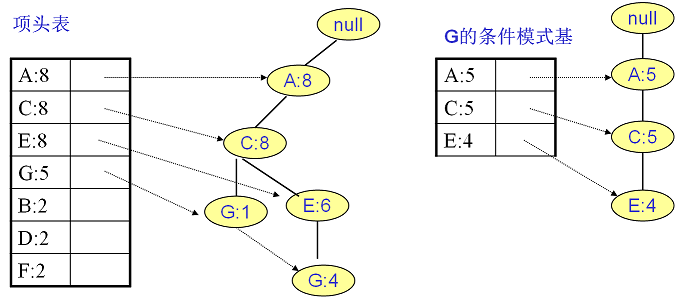
E的条件模式基如下图,递归挖掘到E的最大频繁项集为频繁3项集{A:6, C:6, E:6}。
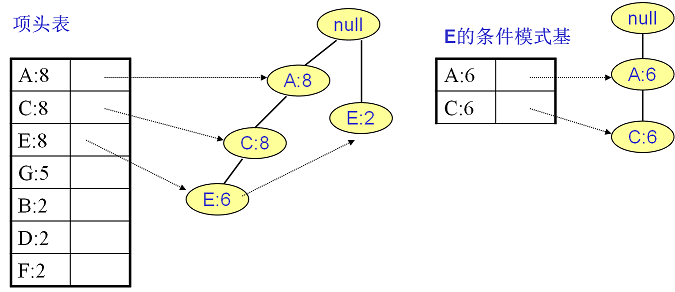
C的条件模式基如下图右边,递归挖掘到C的最大频繁项集为频繁2项集{A:8, C:8}。
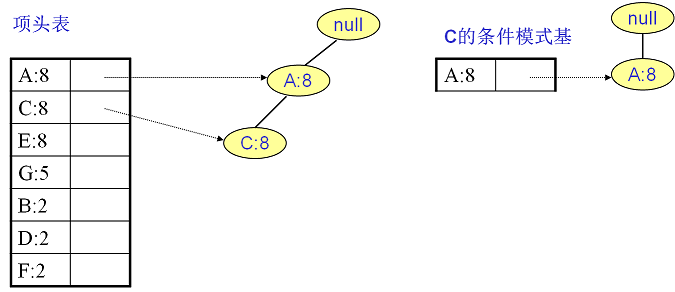
至于A,由于它的条件模式基为空,因此可以不用去挖掘了。
至此我们得到了所有的频繁项集,如果我们只是要最大的频繁K项集,从上面的分析可以看到,最大的频繁项集为5项集。包括{A:2, C:2, E:2,B:2,F:2}。