归并算法详解

        归并算法的本质是将待排序序列分为两部分，依次对分得的两个部分再次使用归并排序，之后再对其进行合并。接下来对待排序列A[0]，A[1]，A[2]，...，A[n-1]，用归并排序思想进行排序。

算法实现：

1.将序列分为两部分，其中一部分对应的索引区间为[start1，end1]；另一部分的对应的索引区间为[start2，end2]。其中，start1 = 0，end1 = （n - 1）/ 2 （向下取整）；

start2 = （n - 1）/ 2 + 1，end2 = n - 1；

2.将上面两个序列按照步骤1再次进行分成四了序列，将四个序列分成八个序列，依次按同样的方法进行下去，知道序列中的元素个数为1时，停止划分序列；

3.将上面所有的序列进行归并排序，排序方法为对所分的n个子序列进行两两合并，得到n/2或n/2+l个含有两个元素的子序列，再对得到的子序列进行合并，直至得到一个长度为n的有序序列为止。

具体流程如下图所示：

 待排序列按步骤1进行划分两个序列如下图：

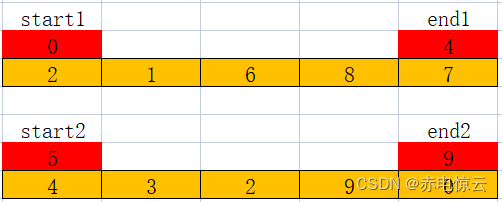
然后将上面2个待排序列化分为4个待排序列如图所示：

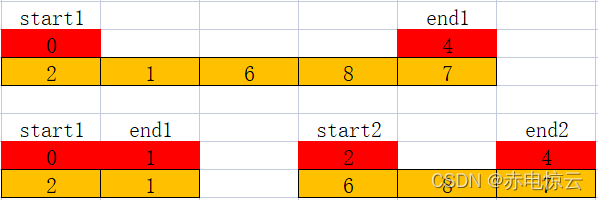
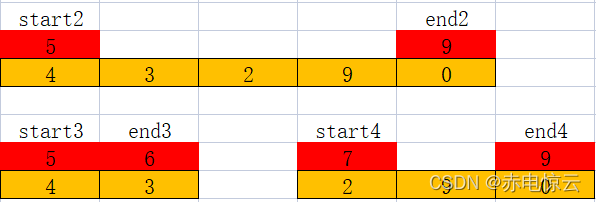
 依次进行划分知道序列中只有一个元素则停止划分：

 划分好后然后进行组合排序：

首先是2个组合排序：

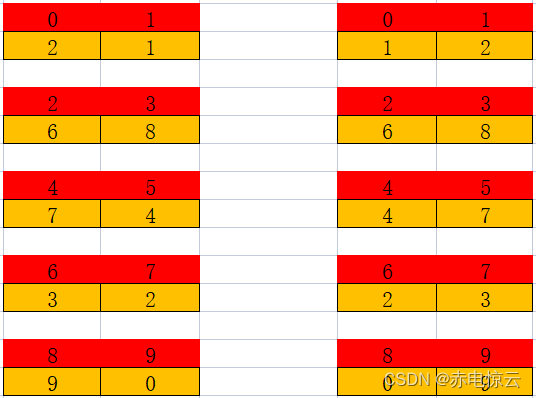
然后再就是4个组合排序：

 依次这样组合排序，知道最后序列长度为n - 1，排序后的结果为：

具体代码实现如下所示：

#include<stdio.h>
#include<stdlib.h>
#define arrNum  10

void merge(int arr[], int low, int mid, int high) 
{
    int i, k;
    int* tmp = (int*)malloc((high - low + 1) * sizeof(int));
    int left_low = low;
    int left_high = mid;
    int right_low = mid + 1;
    int right_high = high;

    for (k = 0; left_low <= left_high && right_low <= right_high; k++)
    {  
        if (arr[left_low] <= arr[right_low]) // 比较两个指针所指向的元素
        {
            tmp[k] = arr[left_low++];
        }
        else 
        {
            tmp[k] = arr[right_low++];
        }
    }

    if (left_low <= left_high)  //若第一个序列有剩余，直接复制出来粘到合并序列尾
    { 
    //memcpy(tmp+k, arr+left_low, (left_high-left_low+l)*sizeof(int));
        for (i = left_low; i <= left_high; i++)
            tmp[k++] = arr[i];
    }

    if (right_low <= right_high) //若第二个序列有剩余，直接复制出来粘到合并序列尾
    {
        //memcpy(tmp+k, arr+right_low, (right_high-right_low+1)*sizeof(int));
        for (i = right_low; i <= right_high; i++)
            tmp[k++] = arr[i];
    }

    for (i = 0; i < high - low + 1; i++)
        arr[low + i] = tmp[i];
    free(tmp);
}

void merge_sort(int arr[], unsigned int first, unsigned int last) 
{
    int mid = 0;
    if (first < last) 
    {
        mid = (first + last) / 2;
        merge_sort(arr, first, mid);
        merge_sort(arr, mid + 1, last);
        merge(arr, first, mid, last);
    }
}

int main() 
{
    int i;
    int a[arrNum] = {2, 1, 6, 8, 7, 4, 3, 2, 9, 0};

    printf("排序前:");
    for (i = 0; i < arrNum; i++)
        printf("%d\t", a[i]);
    printf("\n");

    merge_sort(a, 0, arrNum - 1);  // 排序

    printf("排序后:");
    for (i = 0; i < arrNum; i++)
        printf("%d\t", a[i]); 
    printf("\n");

    system("pause");
    return 0;
}

 代码运行后截图：