题目描述
有n个数字，a[1],a[2],a[3]......a[n]，以及一个数字m。
问n个数字中取出一些数字，这些数字的和能否等于m。
输入
多组测试数据，读入到文件尾结束。
第一行输入n，m。（1<=n<=20, 1<=m<=100）
第二行输入n个数字a[1],a[2],a[3]......a[n]。(1<=a[i]<=100)
输出
如果可以，输出YES，否则输出NO。
样例输入
5 5
1 1 1 1 1
5 5
2 2 2 2 2
样例输出
YES
NO
解决这题的话我们可以观察一下规律:
一个数--两种结果值组合(n的输入为1，m和a[i]不是很重要，咱们讨论的是如何归纳出公式)_
sum1=a[0]*1=a[0]
sum2=a[0]*0=0
两个数--四种结果组合
sum1=a[0]*1+a[1]*1=a[0]+a[1]
sum2=a[0]*1+a[1]*0=a[0]
sum3=a[0]*0+a[1]*0=0
sum4=a[0]*0+a[1]*1=a[1]
三个数、四个数我就不写了，也是这种规律
仔细看看，我们让a[i]乘1能得到a[i]，乘0的话能得到0，正好是我们要不要这个数参与我们的值运算要求。
总结:
sumn=a[0]*b[i]+...+a[i]*b[i](b[i]的值要么就是0,要么就是1)
从上面的分析我们可以总结出sumn的公式，那么能不能用for循环去计算这些值呢，如果用for循环去计算的话，我们可能得弄出个数表来保存b[i]的值，b有好多种排列，比如两个数的话，b这个数组可以为00，01，10，11，这样就很多了，其实就是计算排列什么的，最后把这些排列保存到一个二维数组中，通过这个二维数组来for循环遍历计算，其实这样计算的话时间复杂度是o（2的n次方)，主要是计算排列这一块。用for循环也可以做，但是这里我就不说了。
说说正题：
让我们来用递归去做吧。最主要的就是递归函数这一块的编写。
int digui(int j)
{
if(j==n)//边界条件(递归函数没有边界条件会死循环的）
{
int sum=0;
for(int i=0;i<n;i++)
sum+=b[i]*a[i];//公式模拟
if(sum==m)ok=1;//满足条件OK=1,只要有一个满足条件的就说明完全OK，m是题目中给出的m。
return 1;
}
b[j]=1;//初始这一层的状态
digui(j+1);//往下递归
b[j]=0;
return 0;
}很多人可能想这样写，但是如果这样写的话只会有一个值，因为每次调用函数都会把函数的入口地址和状态保存到栈中(保存现场），那么一直入栈，最后执行完函数出栈，这样的话只会得到一个组合值。
栈的状态
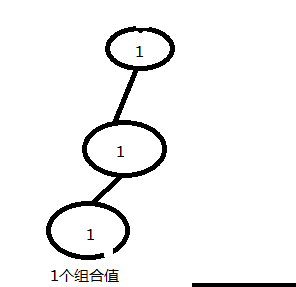只有一个组合值(每个圆圈代表函数，圆圈中的数字代表函数此时b[i]的值）
那么我们来想想，是不是满足这种情况就行了呢？
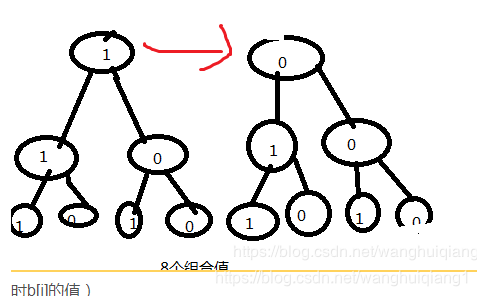
八个组合值(每个圆圈代表函数，圆圈中的数字代表函数此时b[i]的值）
是不是有点像二叉树呢，所以我们需要给他多加一个分支。
int digui(int j)
{
if(j==n)//边界条件(递归函数没有边界条件会死循环的）
{
int sum=0;
for(int i=0;i<n;i++)
sum+=b[i]*a[i];//公式模拟
if(sum==m)ok=1;//满足条件OK=1,只要有一个满足条件的就说明完全OK，m是题目中给出的m。
return 1;
}
b[j]=1;//初始这一层的状态
digui(j+1);//往下回溯
b[j]=0;//为下一次回归来的那一层更新一个新的状态(如果不为回归来的那一层更新状态的话就没意义再多加分支了)
digui(j+1);//往下回溯(像二叉树那样多加一个分支)
return 0;
}这样是不是就大功告成了呢？是的。
下面给出部分栈状态的更新图:
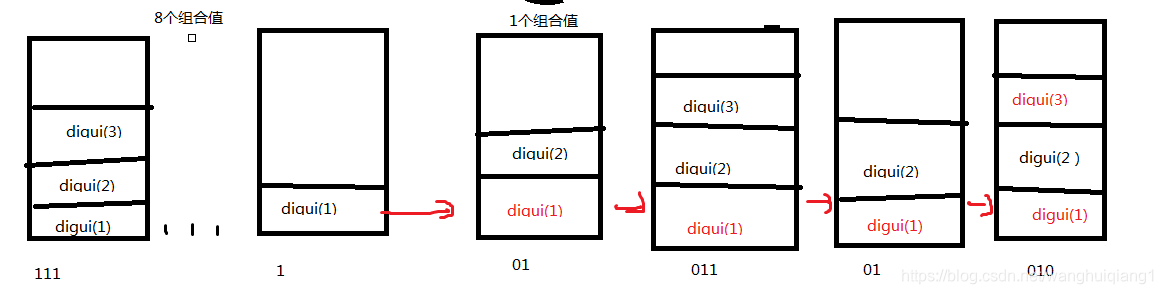
111-》1这一块其实是第一个树的状态更新，我给省略了，1-》010是第一个树到第二个树的更新图，红的函数名称代表着内部b[i]的值为0，黑的函数名称代表着内部b[i]的值为1。
下面是完整代码，
c++版本：
#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;
const int M=10000;
int n,m,a[M],b[M],ok;
int digui(int j)
{
if(j==n)
{
int sum=0;
for(int i=0;i<n;i++)
sum+=b[i]*a[i];
if(sum==m)ok=1;
return 1;
}
b[j]=1;
digui(j+1);
b[j]=0;
digui(j+1);
return 0;
}
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++)cin>>a[i];
digui(0);
if(ok)cout<<"YES";
else cout<<"NO";
return 0;
}C语言版本:
#include <stdio.h>
const int M=10000;
int n,m,a[M],b[M],ok;
int digui(int j)
{
if(j==n)
{
int sum=0;
for(int i=0;i<n;i++)
sum+=b[i]*a[i];
if(sum==m)ok=1;
return 1;
}
b[j]=1;
digui(j+1);
b[j]=0;
digui(j+1);
return 0;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++)scanf("%d",&a[i]);
digui(0);
if(ok)printf("YES");
else printf("NO");
return 0;
}-----------------------------------------------------------------另一种利用全排列的解法(不用看)---------------------------------------------------
#include <iostream>
using namespace std;
const int M=1000;
int book[M];
int a[M];
int n,m,ok;
int fun(int j,int ans)
{ if(ans==m)
{
ok=1;
return 1;
}
if(j==n)return 0;
for(int i=0;i<n;i++)
{
if(!book[i])
{
book[i]=1;
ans+=a[i];
// cout<<"1:"<<ans<<" ";
fun(j+1,ans);
ans-=a[i];
book[i]=0;
}
}
return 0;
}
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++)cin>>a[i];
fun(0,0);
cout<<(ok?"YES":"NO")<<endl;
return 0;
}