最优化：对偶（一）

数学有对称美。

当给定了一个LP，我们总是希望找到另外一个比较对称的LP，使得它和原来的LP之间有比较好的性质。这时候，对偶性(duality)的讨论便出现了。

对偶LP(Dual Linear Program)

对偶性的由来

所谓对偶的LP，一定是原LP有一定的关系。
比如，我们给出下面的一个LP，记其为$P$：
$$\begin{array}{ll}\max & \underset{c}{\underbrace{\left(\begin{array}{llll}4& 9& 2& 4\end{array}\right)}}x\\ \text{ s.t. }& \underset{A}{\underbrace{\left(\begin{array}{cccc}1& -4& 3& 0\\ -1& 7& -5& 1\end{array}\right)}}x=\underset{b}{\underbrace{\left(\begin{array}{l}7\\ 3\end{array}\right)}}\\ & x_1,x_2,x_3,x_4\ge 0\end{array}$$

对于这个LP，它是4元的。我们不能画出这么高维的图形，来规划。因此，人们便在想，能不能使其——这个的4元的问题转化为2元的问题呢？这个问题的答案是：对于这个LP，有。

我们可以利用单纯形法先得到最终的最优解：$(7,0,0,10{)}^T$——对应的最优值为68。
在这里，我们做一个小小的变换，这是一个小trick：
将$AX=b$的constrain 1和constrain 2分别乘于8和4（为叙述方便，记其为$y=(8,4)$），并且相加：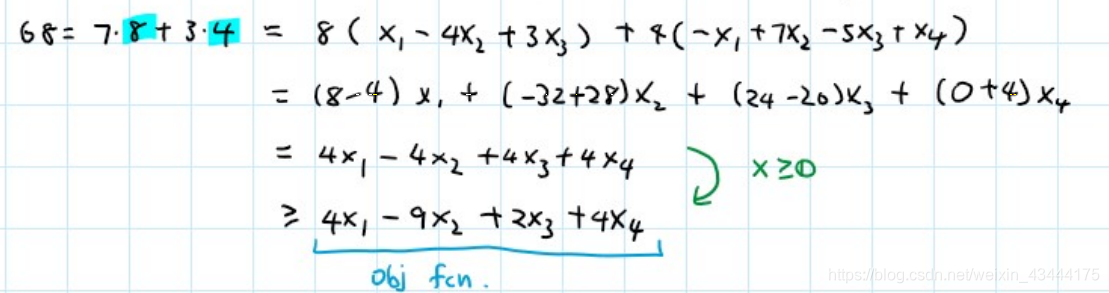

因此，通过放缩，我们可以知道，任何$P$的可行解的值不会超过68。因此，我们可以证明，$(7,0,0,10{)}^T$是一个最优解。因此，我们需要找到一个LP的最优值，问题便转化为了：找到这样的$y$。
但是，可能有人会发问，这也太巧了吧，怎么可能能这么巧呢？因此，蓝底的$(8,4)$便成为关键——怎么找到这样的向量$y$？事实上，我们称这样的$y$为对偶决策变量——相对于原决策变量$x$。

对偶决策变量的寻找

我们以这个例子为例：
首先，从上面的叙述中，我们可以发现，之所以可以放缩，得到这个不等式，原因是我们利用原LP中约束条件的$Ax=b$的$b$与$y$相乘。因此：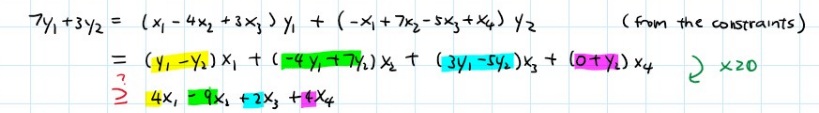

又因为最终不等式，所以黄底、绿底、蓝底和紫底是需要有对应的不等条件的。从而，我们对$y_1$和$y_2$的约束。

发现

其实原LP和其对偶，我们可以发现，在目标函数值，是下图这样的关系：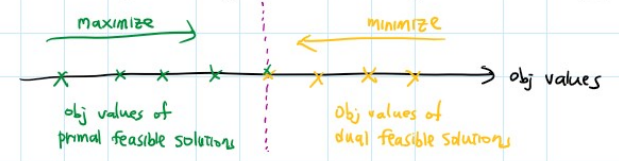
其中，绿色一部分表示原LP，而黄色一部分是其对偶的LP。因此，我们可以发现的是：如果LP和其对偶LP都存在可行解，其可行解会交于一定，这一点便是最终的我们所寻找的最优解（For both primal LP and its dual LP）。因此，引出了下面的两个弱对偶定理和强对偶定理。

弱对偶和强对偶

弱对偶(weak duality)

弱对偶定理叙述如下：
若$\bar{X}$是原LP的可行解，$\bar{Y}$是其对偶问题的可行解，总会有
$$c^T\bar{X}\le b^T\bar{X}$$

强对偶(strong duality)

强对偶定理叙述如下：
若原LP或者其对偶有最优解，那么其对偶问题或原问题也有最优解，且目标值相等。

无界

无界定理：
如果原LP无可行解(No feasible solution)，则其对偶问题无界(unbounded)。
如果对偶问题无可行解，则其原LP无界(unbounded)。

对偶问题的改写