一.BP神经网络

在基于（输入->隐藏层->输出）的基础上，增添反向传播。作为最传统的神经网络，理解它的实现对入门神经网络帮助很大，这里并不会对它的理论进行阐释，而是只谈一些我自己的理解，并附加代码实现。

1.网络架构

相信大家对神经网络的架构都会有基础的了解和认识，它由输入层，隐藏层和输出层构成，输入层的神经元个数与我们输入数据的维度相同（可理解为数据有多少个特征），隐藏层的神经元个数根据具体情况加以设置，输出层神经元个数则与我们要进行拟合的数据个数相同（如二分类问题，则神经元个数为2）。我们喂入样本和标签进入网络 ，网络通过不断更新内部的参数来对数据进行拟合，但是网络并不是直接训练内部的参数，而是使用反向传播，通过对loss值进行训练来更新参数。打个比方来说，我们考试前复习，把本学期的东西全部学习一遍显然是不合适的，这既浪费时间，也会影响我们的学习积极性。更优的做法是重做错题，找到自己的漏洞，有针对性的去突破和训练，而loss值便是神经网络的漏洞。

2.反向传播

loss值，即误差，或者说是神经网络预测出的结果与我们给出标签的偏差。关于反向传播的具体流程，这里有一篇我认为很通俗易懂的博客(反向传播)，顾名思义，反向传播是在神经网络进行一次预测后，通过对loss值的计算，来反向更新神经网络参数的操作。而利用更新后的参数，我们可以进行下一次的训练，得到新一轮的预测，之后再次进行反向传播。

二.PCA降维

即主成分分析，通过提取保留数据的某些主要特征，来对数据进行降维，从而减少输入层神经元的个数。这不仅提升了计算速度，而且通过对某些不重要的特征的剔除，也减小了噪声对训练的影响，提高了模型预测准确率。而这里说的主要特征，说的是最能体现数据与数据之间差异性的特征。打个比方说，你要买一个LOL英雄，英雄的背景对你来说便是无关紧要的特征，你更加看重的是它的技能和价格，而这也正是你用来区分不同英雄的主要特征。但是如果我们将其保留，在我们训练莫得感情的计算机对其分类预测时，那英雄的背景等不重要的特征，就会对分类结果产生些许影响，这些影响或大或小，但终归是我们不想看到的，所以还是删除为好。

三.代码实现

1.制作训练数据

我采用的是Kaggle上的MNIST数据集进行训练 ，数据集下载链接->数据下载
下载完毕后，我们得到三个csv文件，train即Kaggle提供给我们的训练集，test是我们要进行预测的测试集，而sample_submission则是我们进行提交的示例文档格式，这里我把这三个文件统一放到Digit文件夹中。
首先让我们对csv文件进行处理，首先读取训练集。在读取之前，先利用表格自带的排序功能，通过对第一列0~9标签的排序将一种分类的分到一起 ，之后再进行读取，代码如下：

def csv_read_train(data_path):
    data = []; label = []
    with open(data_path, "r") as f:
        reader = csv.reader(f)
        for row in reader:
            data.append(row[1:])
            label.append(row[0])
        data = np.array(data[1:], dtype=int)
        label = np.array(label[1:], dtype=int)
    return data, label

2.PCA降维

def pca_manage(train, n_components):
    print("feature number is --- " + str(n_components))
    pca = PCA(svd_solver='auto', n_components=n_components, whiten=True).fit(train) # 训练一个pca模型
    # print(pca.explained_variance_ratio_)
    with open('pca.pickle','wb') as f:
        pickle.dump(pca, f) # 将模型dump进f里面
    return pca

3.BP神经网络训练

def train():
    # 参数设置
    num_classes = 10 # 输出大小，即分类数
    input_size = 50 # 输入大小，即pca降维后保留的特征数
    hidden_units_size = 2*input_size + 1 # 隐藏层节点数量
    training_iterations = 100000 # 训练轮数，因为有提前中止，所以随便设了很大
    initial_learning_rate = 0.05 # 初始学习率
    
    # 数据读取
    csv_path = "Digit/train.csv"
    data, label = csv_read_train(csv_path)
    m, n = np.shape(data)
    total_y = np.zeros((m, num_classes))
    # print(total_y.shape)
    for i in range(len(label)-1):
        total_y[i][label[i]] = 1
    data = np.round(data / 127.5 - 1) # 数据归一化处理
    x_train, x_test, y_train, y_test = train_test_split(data, total_y, test_size=0.2, random_state=0)
    gr_label = [np.argmax(x) for x in y_test]

    # pca降维
    pca = pca_manage(x_train, input_size)
    x_train_pca = pca.transform(x_train)
    x_test_pca = pca.transform(x_test)
    with open('pca.pickle','rb') as f:
        pca = pickle.load(f)

    # 网络搭建
    X = tf.placeholder(tf.float32, shape = [None, input_size], name='x')
    Y = tf.placeholder(tf.float32, shape = [None, num_classes], name='y')

    W1 = tf.Variable(tf.random_normal([input_size, hidden_units_size], stddev=0.1))
    B1 = tf.Variable(tf.constant (0.1), [hidden_units_size])
    W2 = tf.Variable(tf.random_normal([hidden_units_size, num_classes], stddev=0.1))
    B2 = tf.Variable(tf.constant (0.1), [num_classes])

    hidden_opt = tf.matmul(X, W1) + B1  # 输入层到隐藏层正向传播
    hidden_opt = tf.nn.relu(hidden_opt)  # 激活函数，用于计算节点输出值
    final_opt = tf.matmul(hidden_opt, W2) + B2  # 隐藏层到输出层正向传播
    tf.add_to_collection('pred_network', final_opt) # 便于测试

    # 学习率衰减 在此次训练中作用不是很大  可自行调整
    global_step = tf.Variable(0, trainable=False)
    learning_rate = tf.train.exponential_decay(learning_rate=initial_learning_rate, global_step=global_step, decay_steps=30000, decay_rate=0.5)

    # 对输出层计算交叉熵损失
    loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=Y, logits=final_opt))

    # 梯度下降算法，这里使用了反向传播算法用于修改权重，减小损失
    opt = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss, global_step=global_step)

    # 初始化变量
    sess = tf.Session()
    sess.run(tf.global_variables_initializer())
    saver = tf.train.Saver()

    # 训练
    for i in range(training_iterations):
        training_loss = sess.run([opt, loss, learning_rate], feed_dict={X:x_train_pca, Y:y_train})
        # print(training_loss)
        if i % 10 == 0:
            result = sess.run(final_opt, feed_dict={X:x_test_pca})
            result = [np.argmax(x) for x in result]
            print("step : %d, training loss = %g, accuracy_score = %g, learning_rate = %g" % (i, training_loss[1], metrics.accuracy_score(gr_label, result), training_loss[2]))
            if(metrics.accuracy_score(gr_label, result) > 0.97): # 提前终止，避免过多不必要的训练
                break
    saver.save(sess, './data/bp.ckpt') # 模型保存

训练结果如下：

4.测试及结果存储

由于测试的csv文件和训练的稍有不同（测试的没有标签这一列），所以编写另一段代码来进行读取，代码如下：

def csv_read_test(data_path):
    data = []; label = []
    with open(data_path, "r") as f:
        reader = csv.reader(f)
        for row in reader:
            data.append(row)
        data = np.array(data[1:], dtype=int)
    return data

编写测试结果存储代码，代码如下：

def csv_write(data):
    f = open('result.csv', 'w', encoding='utf-8', newline='')
    csv_writer = csv.writer(f)
    csv_writer.writerow(["ImageId", "Label"])
    for i in range(len(data)):
        csv_writer.writerow([str(i+1), data[i]])

编写BP神经网络的测试部分，代码如下：

def test():
    csv_path = "Digit/test.csv"
    data = csv_read_test(csv_path)
    data = np.round(data / 127.5 - 1) # 数据归一化处理
    with open('pca.pickle','rb') as f: # pca模型读取
        pca = pickle.load(f)
    x_test_pca = pca.transform(data)
    saver = tf.train.import_meta_graph("./data/bp.ckpt.meta")
    with tf.Session() as sess:
        saver.restore(sess, "./data/bp.ckpt")
        graph = tf.get_default_graph()
        x = graph.get_operation_by_name("x").outputs[0]
        y = tf.get_collection("pred_network")[0]
        result = sess.run(y, feed_dict={x:x_test_pca})
        result = [np.argmax(x) for x in result]
        # print(result)
        csv_write(result)
        print('done!!')

之后把result.csv文件投到Kaggle上测试，结果还可以~~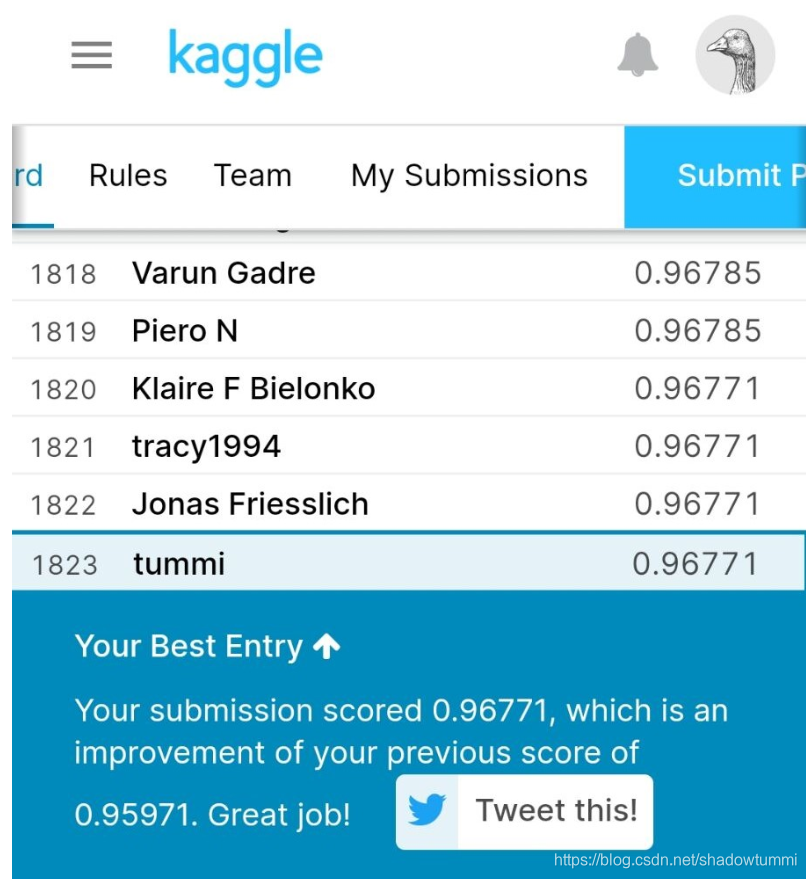

提交的话是需要翻墙的，这个就需要自行解决了。

完整代码

import tensorflow as tf 
# from  tensorflow.examples.tutorials.mnist  import  input_data
import numpy as np
import pickle
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split  #数据集的分割函数
from sklearn import metrics
import csv 

def csv_read_test(data_path):
    data = []; label = []
    with open(data_path, "r") as f:
        reader = csv.reader(f)
        for row in reader:
            data.append(row)
            # label.append(row[0])
        data = np.array(data[1:], dtype=int)
        # label = np.array(label[1:], dtype=int)
        # new_label = np.reshape(label, (-1, 1))
    # x = list(zip(data, new_label))
    # random.shuffle(x)
    # data[:], new_label[:] = zip(*x)
    # return data, label
    return data

def csv_read_train(data_path):
    data = []; label = []
    with open(data_path, "r") as f:
        reader = csv.reader(f)
        for row in reader:
            data.append(row[1:])
            label.append(row[0])
        data = np.array(data[1:], dtype=int)
        label = np.array(label[1:], dtype=int)
        new_label = np.reshape(label, (-1, 1))
    # x = list(zip(data, new_label))
    # random.shuffle(x)
    # data[:], new_label[:] = zip(*x)
    return data, label
    # return data

def csv_write(data):
    f = open('result.csv', 'w', encoding='utf-8', newline='')
    csv_writer = csv.writer(f)
    csv_writer.writerow(["ImageId", "Label"])
    for i in range(len(data)):
        csv_writer.writerow([str(i+1), data[i]])

def pca_manage(train, n_components):
    print("feature number is --- " + str(n_components))
    pca = PCA(svd_solver='auto', n_components=n_components, whiten=True).fit(train)#训练一个pca模型
    # print(pca.explained_variance_ratio_)
    with open('pca.pickle','wb') as f:
        pickle.dump(pca, f) # 将模型dump进f里面
    return pca

def train():
    # 参数设置
    num_classes = 10  # 输出大小
    input_size = 50  # 输入大小
    hidden_units_size = 2*input_size + 1  # 隐藏层节点数量
    training_iterations = 200000
    initial_learning_rate = 0.05

    # 数据读取
    csv_path = "Digit/train.csv"
    data, label = csv_read_train(csv_path)
    m, n = np.shape(data)
    total_y = np.zeros((m, num_classes))
    # print(total_y.shape)
    for i in range(len(label)-1):
        total_y[i][label[i]] = 1
    data = np.round(data / 127.5 - 1)
    x_train, x_test, y_train, y_test = train_test_split(data, total_y, test_size=0.2, random_state=0)
    gr_label = [np.argmax(x) for x in y_test]

    # pca降维
    pca = pca_manage(x_train, input_size)
    x_train_pca = pca.transform(x_train)
    x_test_pca = pca.transform(x_test)
    with open('pca.pickle','rb') as f:
        pca = pickle.load(f)

    # 网络搭建
    X = tf.placeholder(tf.float32, shape = [None, input_size], name='x')
    Y = tf.placeholder(tf.float32, shape = [None, num_classes], name='y')

    W1 = tf.Variable(tf.random_normal([input_size, hidden_units_size], stddev=0.1))
    B1 = tf.Variable(tf.constant (0.1), [hidden_units_size])
    W2 = tf.Variable(tf.random_normal([hidden_units_size, num_classes], stddev=0.1))
    B2 = tf.Variable(tf.constant (0.1), [num_classes])

    hidden_opt = tf.matmul(X, W1) + B1  # 输入层到隐藏层正向传播
    hidden_opt = tf.nn.relu(hidden_opt)  # 激活函数，用于计算节点输出值
    final_opt = tf.matmul(hidden_opt, W2) + B2  # 隐藏层到输出层正向传播
    tf.add_to_collection('pred_network', final_opt)

    # 学习率衰减
    global_step = tf.Variable(0, trainable=False)
    learning_rate = tf.train.exponential_decay(learning_rate=initial_learning_rate, global_step=global_step, decay_steps=30000, decay_rate=0.5)

    # 对输出层计算交叉熵损失
    loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=Y, logits=final_opt))

    # 梯度下降算法，这里使用了反向传播算法用于修改权重，减小损失
    opt = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss, global_step=global_step)

    # 初始化变量
    sess = tf.Session()
    sess.run(tf.global_variables_initializer())
    saver = tf.train.Saver()

    # 训练
    for i in range(training_iterations):
        training_loss = sess.run([opt, loss, learning_rate], feed_dict={X:x_train_pca, Y:y_train})
        # print(training_loss)
        if i % 10 == 0:
            result = sess.run(final_opt, feed_dict={X:x_test_pca})
            result = [np.argmax(x) for x in result]
            print("step : %d, training loss = %g, accuracy_score = %g, learning_rate = %g" % (i, training_loss[1], metrics.accuracy_score(gr_label, result), training_loss[2]))
            if(metrics.accuracy_score(gr_label, result) > 0.97):
                break

    saver.save(sess, './data/bp.ckpt')

def test():
    csv_path = "Digit/test.csv"
    data = csv_read_test(csv_path)
    data = np.round(data / 127.5 - 1)
    with open('pca.pickle','rb') as f:
        pca = pickle.load(f)
    x_test_pca = pca.transform(data)
    saver = tf.train.import_meta_graph("./data/bp.ckpt.meta")
    with tf.Session() as sess:
        saver.restore(sess, "./data/bp.ckpt")
        graph = tf.get_default_graph()
        x = graph.get_operation_by_name("x").outputs[0]
        y = tf.get_collection("pred_network")[0]
        result = sess.run(y, feed_dict={x:x_test_pca})
        result = [np.argmax(x) for x in result]
        # print(result)
        csv_write(result)
        print('done!!')

# train()
test()

参考了很多大神的文章，此处附上链接：

https://zhuanlan.zhihu.com/p/40601434
https://blog.csdn.net/MrMaurice/article/details/90031937
https://blog.csdn.net/weixin_39198406/article/details/82183854