JavaScript基础:(主要介绍三点:简介、特点和组成)
简介:
JavaScript是一种属于网络的脚本语言,已经被广泛用于Web应用开发,常用来为网页添 加各式各样的动态功能,为用户提供更流畅美观的浏览效果。通常JavaScript脚本是通 过嵌入在HTML中来实现自身的功能的。
特点:
1. 解释性脚本语言。 2. 主要用来向HTML页面添加交互行为。 3. 可直接嵌入HTML页面,但写成单独的js文件有利于结构和行为的分离。 4. 跨平台特性,绝大多数浏览器支持,可以在多种平台下运行(如Windows、 Linux、Mac、Android、iOS等)。
组成:
JavaScript由三部分组成:
1. ECMAScript: (3/5/6/7/8)它是JavaScript语言的标准,规定JavaScript的编程语法和 基础核心知识
2. DOM:(document object model)文档对象模型, 提供给JavaScript很多操作页面 中元素的属性和方法
3. BOM:(browser object model)浏览器对象模型, 提供了很多操作浏览器的属性 方法,而这些方法都存放在window浏览器对象上
ECMAScript版本 支持情况
ES5 主流浏览器都支持
ES6(ES2015) 主流浏览器都支持绝大多数功能
ES7(ES2016) 主流浏览器的新版本部分支持
ES8(ES2017) 主流浏览器的新版本部分支持 (摘抄于JavaScript基础)
接下来就介绍一下它的运算符: (算数运算符、赋值运算符、比较运算符和逻辑运算符)
//算术运算符
var x = 5; var y = 2;
console.log("x+y=" + (x + y)); console.log("x-y=" + (x - y));
console.log("x*y=" + (x * y)); console.log("x/y=" + (x / y));
console.log("x%y=" + (x % y));
//JavaScript当除数为0是
console.log(1/0);// Infinity 正无穷 console.log(0/0);//NaN 非数console.log(-1/0);//-Infinity 负无穷 console.log(1%0);// NaN
console.log(0%0);// NaN console.log(-1%0);// NaN
当JavaScript除数为0时,JS中不会报错,但是得到的值有点特殊(当大于0的数除0时结果等于正无穷Infinity、0除0等于NaN非数、小于0的数除0时结果为负无穷-Infinity、之后凡是取余的情况下除数为0的通通都是NaN非数),
对应输出值图如下: (没什么很难得问题点,易懂)
//赋值运算符 (把加减乘除取余和等号组合)
x = 5; y = 2;
x += y;// x=x+y; x -= y;// x=x-y; x *= y;// x=x*y;
x /= y;// x=x/y; x %= y;// x=x%y;
console.log(x);
把后面那一个的值赋给前面那一个就叫赋值。
当y等于0时x /= y和x %= y就要参考上面的除数为0的情况。
//比较运算符 (举了4个比较难理解的例子)
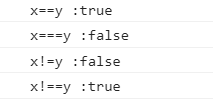
x = "123"; y = 123;
console.log("x==y :" + (x == y)); ==只比较值,类型不管 (相等) true
console.log("x===y :" + (x === y)); ===先比较类型,如果类型相同再比较值,值不同还是不等(绝对相等) false
console.log("x!=y :" + (x != y)); !=直接比较值相不相等 false
console.log("x!==y :" + (x !== y)); !==先比较类型,不同就是true了,类型不同再比较值,值也相同就是false了。 true
注意:
===和!== 首先比较两边的变量数据类型是否相同,如果类型相同才会比较两边 的变量的数值是否相等; ==和!= 比较时,若两边的类型不同会偿试转换类型,然后比较两边变量的数值 是否相等;若两边的类型相同,直接比较两边的数值是否相同。
//逻辑运算符 (&&、||、!)
x=5; y=6; z=7;
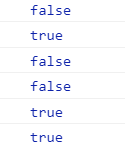
console.log((x<y)&&(x>z)); console.log((x<y)||(x>z)); console.log(!(x<y));
简化版:
console.log(true && false); console.log(true || false); console.log(!false);//非