本文主要分析Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Network论文中提出的新的图神经网络模型以及新的训练图神经网络的训练方法。
一些经典模型如 GCN 采用了 full-batch 的 SGD 优化算法,要计算整个梯度则需要存储所有中间的 Embedding,因此,其是不可扩展的。此外,虽然每个 epoch 也只能更新一次参数。
GraphSAGE 中提出 mini-batch 的 SGD 优化方法,由于每次更新只基于一个 mini-batch,所以内存的需求降低,并在每个 epoch 中可以进行多次更新,从而收敛速度更快。然而,随着层数加深,每个节点的感受野越来越大,其计算单个节点的计算开销也会越来越大。针对这个问题,GraphSAGE 通过使用固定大小的邻居采样,同时 FastGCN 的重要性采样可以一定程度上解决计算开销,但是随着 GCN 的深度加深,计算开销问题依然没法解决。VR-GCN 提出利用方差来控制邻居的采样节点,尽管减少了采样的大小,但是它需要将所有节点的中间 Embedding 存储于内存中,导致其可扩展性较差。
下表是不同模型的时间复杂度和空间复杂度:
作者在实验中发现mini-batch的算法效率与batch内节点与batch外节点间的连接数量成正比,针对这一现象,作者构建了节点的分区,使同一分区中的节点之间的图连接于不同分区中的节点之间的图连接更多。
为了解决普通方法无法在超大图上做节点表征学习的问题,Cluster-GCN论文提出:
- 利用图节点聚类算法将一个图的节点划分为c个簇,每一次选择几个组的节点和这些节点对应的边构成一个子图,然后对子图做训练。
- 由于是利用图节点聚类算法将节点划分为多个簇,所以簇内边的数量要比簇间边的数量多得多。
- 基于小图进行训练,不会消耗很多内存空间,于是我们可以训练更深的神经网络,从而得到更高的精度。
我们知道,基于mini-batch的SGD可以在单个epoch中更新多次,从而使得其比full batch具有更快的收敛速度,但是前者每个epoch所花的时间都更长。
原理
对于一个图G而言,将其分为c组,其中只包含组内节点之间的边,对节点进行重组后,邻接矩阵被划分为c的平方个子矩阵,即
其中
对角线每个块都是大小为|Vt|x|Vt|的邻接矩阵,它由Gt内的边构成。 ∆是由A的所有非对角线块组成的矩阵。Xt和Yt分别由Vt中节点的特征和标签组成。
划分簇的意义:
- 对于每个batch而言,Embedding utilization相当于簇内的连接,每个节点及其相邻节点通常位于同一簇内,因此经过几次后跳跃后,邻接节点大概率还是在簇内;
- 我们使用它的块对角线近似值来替换了原来的矩阵,并且误差与簇间的的连接成正比,所以需要使得簇间的连接数量尽可能少。
下图为图的随机分区与聚类分区的对比: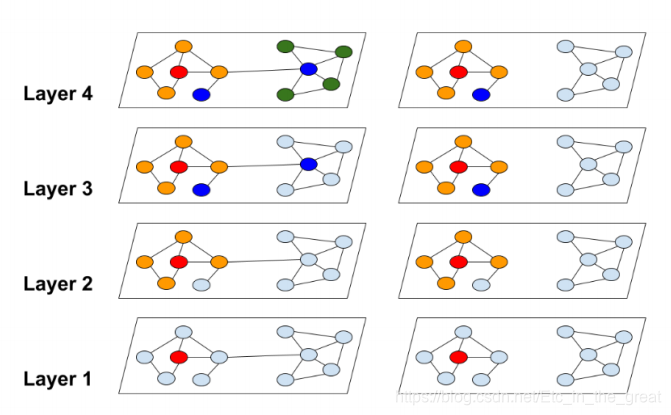
随机多分类
尽管 vanilla Cluster-GCN 能够减少计算开销和内存开销,但仍然存在两个问题:
- 图被分割后,原来图中的一些连接会被删除,影响性能。
- 聚类后的分布与原始数据集有区别,从而导致 SGD 更新时有偏差。
下图为 Reddit 数据集中标签分布不平衡的案例,通过每个簇的标签分布计算其熵值,与随机分割相比,可以清楚的看到聚类分区的簇的熵较小,这表明簇的标签分布偏向于某些特征的标签,所以这会增加不同 batch 的梯度更新的差异,并影响 SGD 的收敛性。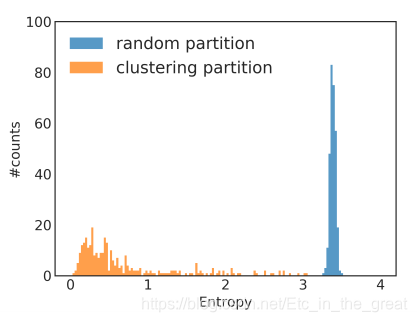
为了解决这个问题,作者提出随机多聚类方法对簇进行合并,从而减少batch间的差异。
作者首先将图分为多个小簇,然后随机选择q个簇并到batch中,这样可以减少batch之间的差异。
下图展示了每个epoch随机组合的batch,相同颜色的块在同一数据batch中: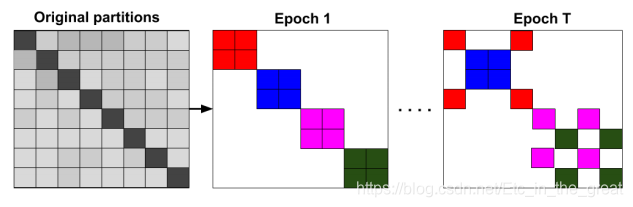
两种方式对比,随机多聚类方法收敛速度更快: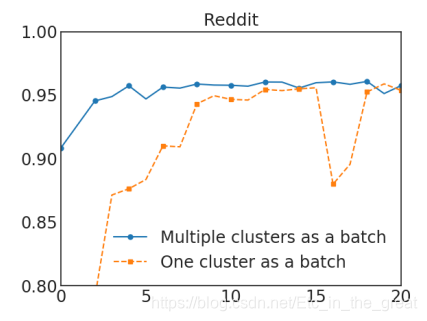
作者提出了一个简单的技术来改进深度 GCN 的训练,核心思想在于放大每个 GCN 层中使用的邻接矩阵 A 的对角部分,并通过这种方式在每个 GCN 层的聚合中对上一层的 Embedding 添加更多的权重:但这种方法有些问题,比如这种方法无视相邻节点的数量,而对所有节点使用相同的权重。此外,当层数增加时,其数值可能会呈现指数型爆炸。所以作者先对邻接矩阵进行标准化。
实现
1.数据集分析
dataset = Reddit('../dataset/Reddit')
data = dataset[0]
# print(dataset.num_classes)
# print(data.num_nodes)
# print(data.num_edges)
# print(data.num_features)
可以看到该数据集包含41个分类任务,232965个节点,114615873条边,节点维度为602维。
2.图节点聚类和数据加载器生成
cluster_data = ClusterData(data, num_parts=1500, recursive=False, save_dir=dataset.processed_dir)
train_loader = ClusterLoader(cluster_data, batch_size=20, shuffle=True, num_workers=0)
subgraph_loader = NeighborSampler(data.edge_index, sizes=[-1], batch_size=1024, shuffle=False, num_workers=0)
train_loader:图节点首先被聚类,返回的一个batch由多个簇组成
subgraph_loader:使用此数据加载器不对图节点聚类,计算一个batch中的节点的嵌入需要计算该batch中所有节点的距离从0到L的邻居节点。
3.构建神经网络
class Net(torch.nn.Module):
def __init__(self, in_channels, out_channels):
super(Net, self).__init__()
self.convs = ModuleList([SAGEConv(in_channels, 128), SAGEConv(128, out_channels)])
def forward(self, x, edge_index):
for i,conv in enumerate(self.convs):
x = conv(x, edge_index)
if i != len(self.convs) - 1:
x = F.relu(x)
x = F.dropout(x, p=0.5, training=self.training)
return F.log_softmax(x, dim=-1)
def inference(self, x_all):
pbar = tqdm(total=x_all.size(0)*len(self.convs))
pbar.set_description('Evaluating')
for i,conv in enumerate(self.convs):
xs = []
for batch_size, n_id, adj in subgraph_loader:
edge_index, _, size = adj.to(device)
x = x_all[n_id].to(device)
x_target = x[:size[1]]
x = conv((x, x_target), edge_index)
if i != len(self.convs) - 1:
x = F.relu(x)
xs.append(x.cpu())
pbar.update(batch_size)
x_all = torch.cat(xs, dim=0)
pbar.close()
return x_all
4.最后我们对网络进行训练,5个epoch验证一次,结果如下:

loss从0.3358降到了0.2313,测试集的准确率大概到了94.56%左右。
作业
将数据集切分成不同数量的簇进行实验,观察结果并进行比较。
1.将数据集分成1000簇,最后的正确率为94.56%。
2.将数据集分成2000簇
参考资料
1.https://cloud.tencent.com/developer/article/1665684
2.超大图上的表征学习