本章主要介绍了直接法和光流法。

意义：

1. 关键点的提取和描述子的计算十分耗时

2. 使用特征点时忽略除了特征点以外所有的信息

3. 相机可能运动到特征缺失的地方

4. 直接法还具有恢复稠密或半稠密机构的能力

LK光流：计算像素的运动

注：LK光流只是描述了两个图像之间的运动关系，并没有得出R、t

单层光流理论

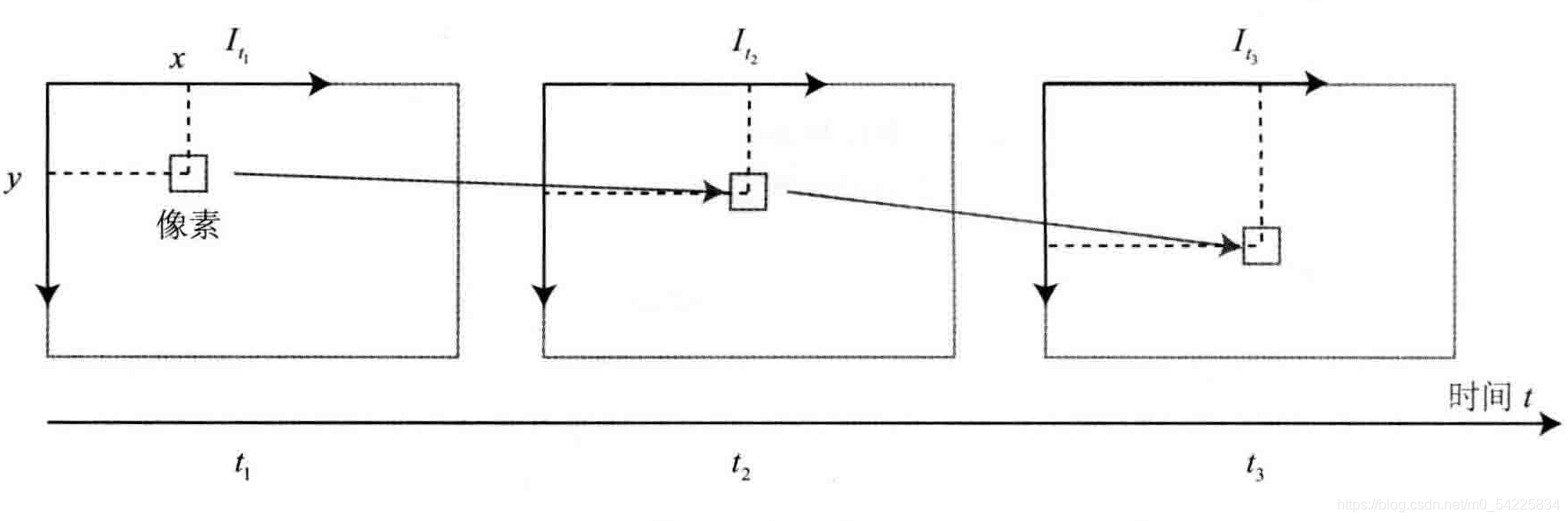
 假设：

1. 同一个空间点在不同图像的灰度值相同（假设性较强）

2. 某一窗口内的像素具有相同的运动

 实践

opencv实现

    vector<Point2f> pt1, pt2;
    for (auto &kp: kp1) pt1.push_back(kp.pt);
    vector<uchar> status;
    vector<float> error;
    cv::calcOpticalFlowPyrLK(img1, img2, pt1, pt2, status, error);

 只需使用cv::calcOpticalFlowPyrLK()函数并提供，两张图片及对应特征点

 高斯牛顿法

把问题转化为

对应的梯度是第二个图像在处的梯度

1. 算出误差

double error = GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y) -
               GetPixelValue(img2, kp.pt.x + x + dx, kp.pt.y + y + dy);
//kp.pt.x+x表示第x个关键点的x坐标

2.计算雅可比：算的是以(x,y)为中心，以2*half_patch_size为边的正方形里每一个点的梯度值（两层for循环）

if (inverse == false) {//图像2在x，y处的梯度：(f(x+1)-f(x-1))/2
   J = -1.0 * Eigen::Vector2d(
   0.5 * (GetPixelValue(img2, kp.pt.x + dx + x + 1, kp.pt.y + dy + y) -
   GetPixelValue(img2, kp.pt.x + dx + x - 1, kp.pt.y + dy + y)),
   0.5 * (GetPixelValue(img2, kp.pt.x + dx + x, kp.pt.y + dy + y + 1) -
   GetPixelValue(img2, kp.pt.x + dx + x, kp.pt.y + dy + y - 1))
    );
}

3. 计算H，b：H和b是正方形里所有点算出来的和（实际上这几个点占的区域很小，可以看成一个点）

                    b += -error * J;
                    cost += error * error;
                    if (inverse == false || iter == 0) {
                        // also update H
                        H += J * J.transpose();
                    }

4. 高斯牛顿解决

Eigen::Vector2d update = H.ldlt().solve(b);
// update dx, dy
dx += update[0];
dy += update[1];
lastCost = cost;

多层光流理论

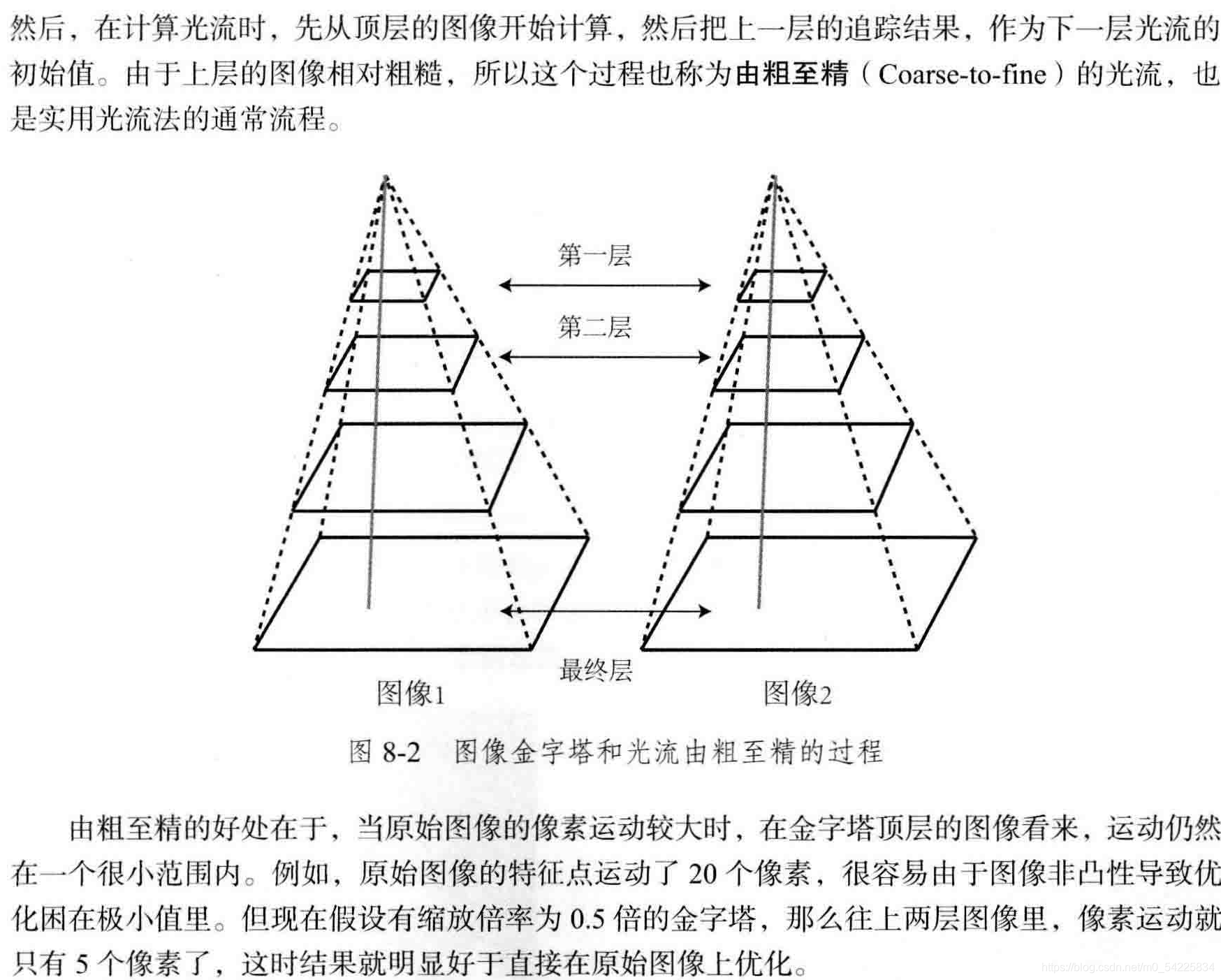
 代码

 1. 创建三角：0~5表示初始图像，缩放倍率为0.5 的图像……

    vector<Mat> pyr1, pyr2; // image pyramids
    for (int i = 0; i < pyramids; i++) {
        if (i == 0) {
            pyr1.push_back(img1);
            pyr2.push_back(img2);
        } else {
            Mat img1_pyr, img2_pyr;
            cv::resize(pyr1[i - 1], img1_pyr,
                       cv::Size(pyr1[i - 1].cols * pyramid_scale, pyr1[i - 1].rows * pyramid_scale));
            cv::resize(pyr2[i - 1], img2_pyr,
                       cv::Size(pyr2[i - 1].cols * pyramid_scale, pyr2[i - 1].rows * pyramid_scale));
            pyr1.push_back(img1_pyr);
            pyr2.push_back(img2_pyr);
        }
    }

2. 对每一层图像进行单层光流，并为下一层初始化

    for (int level = pyramids - 1; level >= 0; level--) {
        // from coarse to fine
        success.clear();
        t1 = chrono::steady_clock::now();
        OpticalFlowSingleLevel(pyr1[level], pyr2[level], kp1_pyr, kp2_pyr, success, inverse, true);//对每一层进行单层光流
        t2 = chrono::steady_clock::now();
        auto time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
        cout << "track pyr " << level << " cost time: " << time_used.count() << endl;
        //为下一层初始化
        if (level > 0) {
            for (auto &kp: kp1_pyr)
                kp.pt /= pyramid_scale;
            for (auto &kp: kp2_pyr)
                kp.pt /= pyramid_scale;
        }
    }

总结：

光流法科研加速基于特征点的视觉里程计，避免计算和匹配描述子的过程，但要求相机运动比较平滑。 

直接法

单层直接法理论

问题：已知p1,P,位姿1，求第二个位姿使最小（一般是使用RGB-D或者双目快速获得深度）

即

令q=TP,  u=Kq/Z 

J= =

 其中：
 

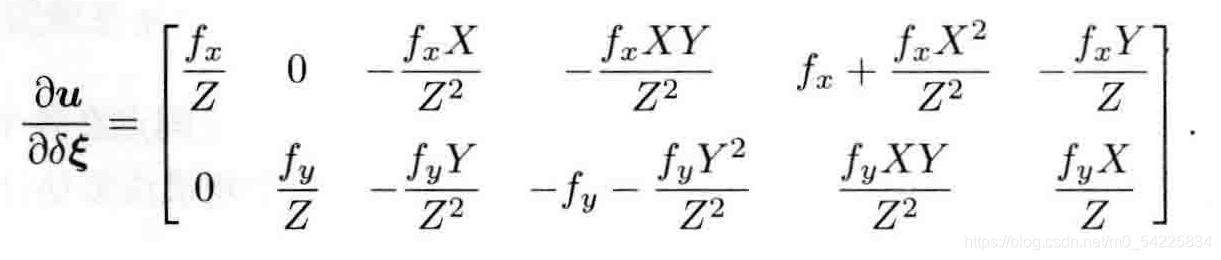
代码

 1. 计算p1对应的空间点P，并使用初始的T转换到p2所在的坐标系，即：q=T*p

Eigen::Vector3d point_ref =
depth_ref[i] * Eigen::Vector3d((px_ref[i][0] - cx) / fx, (px_ref[i][1] - cy) / fy, 1);
Eigen::Vector3d point_cur = T21 * point_ref;

 2. 确定参数

        projection[i] = Eigen::Vector2d(u, v);
        double X = point_cur[0], Y = point_cur[1], Z = point_cur[2],
            Z2 = Z * Z, Z_inv = 1.0 / Z, Z2_inv = Z_inv * Z_inv;


                double error = GetPixelValue(img1, px_ref[i][0] + x, px_ref[i][1] + y) -
                               GetPixelValue(img2, u + x, v + y);
                Matrix26d J_pixel_xi;
                Eigen::Vector2d J_img_pixel;

                J_pixel_xi(0, 0) = fx * Z_inv;
                J_pixel_xi(0, 1) = 0;
                J_pixel_xi(0, 2) = -fx * X * Z2_inv;
                J_pixel_xi(0, 3) = -fx * X * Y * Z2_inv;
                J_pixel_xi(0, 4) = fx + fx * X * X * Z2_inv;
                J_pixel_xi(0, 5) = -fx * Y * Z_inv;

                J_pixel_xi(1, 0) = 0;
                J_pixel_xi(1, 1) = fy * Z_inv;
                J_pixel_xi(1, 2) = -fy * Y * Z2_inv;
                J_pixel_xi(1, 3) = -fy - fy * Y * Y * Z2_inv;
                J_pixel_xi(1, 4) = fy * X * Y * Z2_inv;
                J_pixel_xi(1, 5) = fy * X * Z_inv;

 3. 求

J_img_pixel = Eigen::Vector2d(
0.5 * (GetPixelValue(img2, u + 1 + x, v + y) - GetPixelValue(img2, u - 1 + x, v + y)),
0.5 * (GetPixelValue(img2, u + x, v + 1 + y) - GetPixelValue(img2, u + x, v - 1 + y))
);

 4. 求J、H、b

Vector6d J = -1.0 * (J_img_pixel.transpose() * J_pixel_xi).transpose();
hessian += J * J.transpose();
bias += -error * J;
cost_tmp += error * error;

 5. 叠加

    if (cnt_good) {
        // set hessian, bias and cost
        unique_lock<mutex> lck(hessian_mutex);
        H += hessian;
        b += bias;
        cost += cost_tmp / cnt_good;
    }

多层也差不多，就不写了

直接法的优缺点

补： 

// bilinear interpolation
inline float GetPixelValue(const cv::Mat &img, float x, float y) {
    // boundary check
    if (x < 0) x = 0;
    if (y < 0) y = 0;
    if (x >= img.cols) x = img.cols - 1;
    if (y >= img.rows) y = img.rows - 1;
    uchar *data = &img.data[int(y) * img.step + int(x)];
    float xx = x - floor(x);
    float yy = y - floor(y);
    return float(
        (1 - xx) * (1 - yy) * data[0] +
        xx * (1 - yy) * data[1] +
        (1 - xx) * yy * data[img.step] +
        xx * yy * data[img.step + 1]
    );
}

opencv
在图像img2上画图    
cv::cvtColor(img2, img2_single, CV_GRAY2BGR);
    for (int i = 0; i < kp2_single.size(); i++) {
        if (success_single[i]) {
            cv::circle(img2_single, kp2_single[i].pt, 2, cv::Scalar(0, 250, 0), 2);
            cv::line(img2_single, kp1[i].pt, kp2_single[i].pt, cv::Scalar(0, 250, 0));
        }
    }

修改图像的分辨率
cv::resize(pyr1[i - 1], img1_pyr,
                       cv::Size(pyr1[i - 1].cols * pyramid_scale, pyr1[i - 1].rows * pyramid_scale));

cv::parallel_for_(cv::Range(0, px_ref.size()),
                          std::bind(&JacobianAccumulator::accumulate_jacobian, &jaco_accu, std::placeholders::_1));
//多线程运行accumulate_jacobian，运行px_ref.size()次，线程不定