
 源:学科网] 【要点梳理】 要点一、命题的概念 用语言、符号或式子表达
源:学科网] 【要点梳理】 要点一、命题的概念 用语言、符号或式子表达 的,可以判断真假的陈述句叫做命题.其中判断为真的语句叫真命题,判断为假的语句叫假命题. 要点诠释: 1. 不是任何语句都是命题,不能确定真假的语句不是命题,如“
的,可以判断真假的陈述句叫做命题.其中判断为真的语句叫真命题,判断为假的语句叫假命题. 要点诠释: 1. 不是任何语句都是命题,不能确定真假的语句不是命题,如“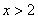 ”,“2不一定大于3”. 2. 只有能够判断真假的陈述句才是命题.祈使句,疑问句,感叹句都不是命题,例如:“起立”、“是有理数吗?”、“今天天气真好!”等. 3. 语句能否确定真假是判断其是否是命题的关键.一个命题要么是真,要么是假,不能既真又假,模棱两可.命题陈述了我们所思考的对象具有某种属性,或者不具有某种属性,这类似于集合中元素的确定性. 要点二、命题的结构 命题可以改写成“若
”,“2不一定大于3”. 2. 只有能够判断真假的陈述句才是命题.祈使句,疑问句,感叹句都不是命题,例如:“起立”、“是有理数吗?”、“今天天气真好!”等. 3. 语句能否确定真假是判断其是否是命题的关键.一个命题要么是真,要么是假,不能既真又假,模棱两可.命题陈述了我们所思考的对象具有某种属性,或者不具有某种属性,这类似于集合中元素的确定性. 要点二、命题的结构 命题可以改写成“若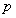 ,则
,则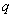 ”的形式,或“如果
”的形式,或“如果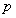 ,那么
,那么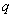 ”的形式.其中
”的形式.其中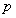 是命题的条件,
是命题的条件,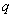 是命题的结论. 要点诠释: 1. 一般地,命题“若p则q”中的p为命题的条件q为命题的结论. 2. 有些问题中需要明确指出条件p和q各是什么,因此需要将命题改写为“若p则q”的形式. 要点三、四种命题 原命题:“若
是命题的结论. 要点诠释: 1. 一般地,命题“若p则q”中的p为命题的条件q为命题的结论. 2. 有些问题中需要明确指出条件p和q各是什么,因此需要将命题改写为“若p则q”的形式. 要点三、四种命题 原命题:“若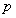 ,则
,则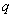 ”; 逆命题:“若
”; 逆命题:“若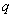 ,则
,则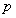 ”;实质是将
”;实质是将 原命题的条件和结论互相交换位置; 否命题:“若非
原命题的条件和结论互相交换位置; 否命题:“若非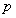 ,则非
,则非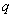 ”,或“若
”,或“若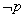 ,则
,则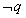 ”;实质是将原命题的条件和结论两者分别否定; 逆否命题:“若非
”;实质是将原命题的条件和结论两者分别否定; 逆否命题:“若非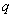 ,则非
,则非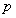 ”,或“若
”,或“若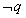 ,则
,则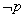 ”;实质是将原命题的条件和结论两者分别否定后再换位或将原命题的条件和结
”;实质是将原命题的条件和结论两者分别否定后再换位或将原命题的条件和结 论换位后再分
论换位后再分 别否定. 要点诠释: 对于一般的数学命题,要先将其改写为“若
别否定. 要点诠释: 对于一般的数学命题,要先将其改写为“若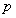 ,则
,则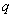 ”的形式,然后才方便写出其他形式的命题. 要点四、四种命题之间的关系 四种命题之间的构成关系
”的形式,然后才方便写出其他形式的命题. 要点四、四种命题之间的关系 四种命题之间的构成关系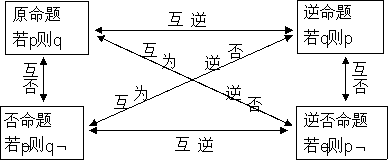 四种命题之间的真值关系
四种命题之间的真值关系原 命题 命题 | 逆命题 | 否命题 | 逆否命题 |
| 真 | 真 | 真[来源:Z+xx+k.Com] | 真 |
| 真 | 假 | 假 | 真 |
| 假[来源:学科网] | 真 | 真 | 假 |
| 假 | 假 | 假 | 假 |
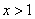 ; (2) 当
; (2) 当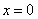 时,
时, 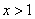 ; (3) 你是男生吗? (4) 求证:
; (3) 你是男生吗? (4) 求证: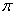 是无理数. 【答案】 (1) 不是命题;由于无法确定变量
是无理数. 【答案】 (1) 不是命题;由于无法确定变量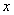 的值,所以无法确定其真假. (2) 是命题;假命题. (3) 不是命题;这是一个疑问句,没有做出判断. (4) 不是命题;这是一个祈使句,没有做出判
的值,所以无法确定其真假. (2) 是命题;假命题. (3) 不是命题;这是一个疑问句,没有做出判断. (4) 不是命题;这是一个祈使句,没有做出判 断. 【变式2】下列语句中是命题的是( ) A.
断. 【变式2】下列语句中是命题的是( ) A.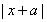 B.{0}∈N C.元素与集合 D.真子集 【答案】B 【变式
B.{0}∈N C.元素与集合 D.真子集 【答案】B 【变式 3】判断下列语
3】判断下列语 句是否是命题. (1)这是一棵大树;[来源:学#科#网] (2)sin30=
句是否是命题. (1)这是一棵大树;[来源:学#科#网] (2)sin30=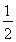 ; (3)x2+1>0; (4)梯形是平行四边形. 【答案】 (1)不是,无法确定“大”;(2)是;(3)是;(4)是. 类型二:命题的结构 例2.指出下面命题的条件和结论. (1)对顶角相等; (2) 四边相等的四边形是菱形. 【思路点拨】 命题都是一定的条件下推出的一定的结果,所以据此确定哪是条件,哪是结论。 【解析】(1)原命题写成:若两个角是对顶角,则这两个角相等.条件:两个角是对顶角;结论:这两个角相等.[来源:学,科,网Z,X,X,K] (2)原命题可写成:如果一个四边形的四边相等,则这
; (3)x2+1>0; (4)梯形是平行四边形. 【答案】 (1)不是,无法确定“大”;(2)是;(3)是;(4)是. 类型二:命题的结构 例2.指出下面命题的条件和结论. (1)对顶角相等; (2) 四边相等的四边形是菱形. 【思路点拨】 命题都是一定的条件下推出的一定的结果,所以据此确定哪是条件,哪是结论。 【解析】(1)原命题写成:若两个角是对顶角,则这两个角相等.条件:两个角是对顶角;结论:这两个角相等.[来源:学,科,网Z,X,X,K] (2)原命题可写成:如果一个四边形的四边相等,则这 个四边形是菱形.条件:一个四边形的四边相等;结论
个四边形是菱形.条件:一个四边形的四边相等;结论 :这个四边形是菱形. 【总结升华】要写出一个命题的条件和结论,一般是把一个命题改写成“如果p,那么q”的形式,其中p是条件,q是结论. 举一反三: 【变式】指出下列命题的条件p和结论q. (1)若空间四边形为正四面体,则顶点在底面上的射影为底面的中心; (2)若两条直线a和b都和直线c平行,则直线a和直线b平行.
:这个四边形是菱形. 【总结升华】要写出一个命题的条件和结论,一般是把一个命题改写成“如果p,那么q”的形式,其中p是条件,q是结论. 举一反三: 【变式】指出下列命题的条件p和结论q. (1)若空间四边形为正四面体,则顶点在底面上的射影为底面的中心; (2)若两条直线a和b都和直线c平行,则直线a和直线b平行. 【答案】[来源:Zxxk.Com] (1)条件p:空间四边形为正四面体;结论
【答案】[来源:Zxxk.Com] (1)条件p:空间四边形为正四面体;结论 q:顶点在底面上的射影为底面的中心. (2)条件p:两直线a、b都和直线c平行;结论q:直线a和b平行. 例3. 将下列命题改写为“若p,则q”的形式,并判断其真假. (1)垂直于同一条直线的两个平面互相平行; (2)对角线相等的平面四边形是矩形. 【解析】 (1)“若两个平面垂直于同一条直线,则这两个平面平行”,真命题. (2
q:顶点在底面上的射影为底面的中心. (2)条件p:两直线a、b都和直线c平行;结论q:直线a和b平行. 例3. 将下列命题改写为“若p,则q”的形式,并判断其真假. (1)垂直于同一条直线的两个平面互相平行; (2)对角线相等的平面四边形是矩形. 【解析】 (1)“若两个平面垂直于同一条直线,则这两个平面平行”,真命题. (2 )“若一个平面四边形的两条对角线相等,则这个四边形是矩形”,假命题. 【总结升华】有一些命题虽然表面上不是“若p,则q”的形式,但适当的改写后可以写成“若p,则q”的形式,那么就能很清楚地看出其条件和结论. 举一反三: 【变式1】把命题“6是12和24的公约数”写成若p则q的形式. 【答案】若一个数等于6,则这个数是12和24的公约数. 【变式2】将下列命题改写成“若p则q”的形式,并判断真假. (1)偶数能被2整除; (2)奇函数的图象关于原点对称; (3)同弧所对的圆周角不相等. 【答案】 (1)若一个数是偶数,则它能被2整除;真命题. (2)若一个函数是奇函数,则它的图象关于原点对称;真命题.[来源:学科网ZXXK] (3)若两个角为同弧所对的圆周角,则它们不相等;假命题. 类型三:命题的四种形式
)“若一个平面四边形的两条对角线相等,则这个四边形是矩形”,假命题. 【总结升华】有一些命题虽然表面上不是“若p,则q”的形式,但适当的改写后可以写成“若p,则q”的形式,那么就能很清楚地看出其条件和结论. 举一反三: 【变式1】把命题“6是12和24的公约数”写成若p则q的形式. 【答案】若一个数等于6,则这个数是12和24的公约数. 【变式2】将下列命题改写成“若p则q”的形式,并判断真假. (1)偶数能被2整除; (2)奇函数的图象关于原点对称; (3)同弧所对的圆周角不相等. 【答案】 (1)若一个数是偶数,则它能被2整除;真命题. (2)若一个函数是奇函数,则它的图象关于原点对称;真命题.[来源:学科网ZXXK] (3)若两个角为同弧所对的圆周角,则它们不相等;假命题. 类型三:命题的四种形式 例4.写出下列命题的逆命题、否命题、逆否命题,并判断四种命题的真假. (1)若
例4.写出下列命题的逆命题、否命题、逆否命题,并判断四种命题的真假. (1)若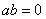 ,则
,则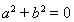 ; (2)若
; (2)若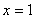 ,则
,则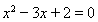 ; (3)若一个三角形有两条边相等,则这个三角形有两个角相等. 【思路点拨】 由原命题写出逆命题,否命题和逆否命题时注意规律: ①交换原命题的条件和结论.所得命题就是逆命题. ②同时否定原命题的条件和结论所得命题就是否命题. ③交换原命题的条件和结论并且同时否定.所得命题就是逆否命题. 【解析】 (1) 原命题:若
; (3)若一个三角形有两条边相等,则这个三角形有两个角相等. 【思路点拨】 由原命题写出逆命题,否命题和逆否命题时注意规律: ①交换原命题的条件和结论.所得命题就是逆命题. ②同时否定原命题的条件和结论所得命题就是否命题. ③交换原命题的条件和结论并且同时否定.所得命题就是逆否命题. 【解析】 (1) 原命题:若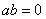 ,则
,则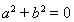 ; 假命题 逆命题:若
; 假命题 逆命题:若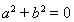 ,则
,则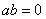 ;
;  真命题 否命题:若
真命题 否命题:若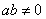 ,则
,则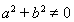 ; 真命题 逆否命题:若
; 真命题 逆否命题:若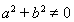 ,则
,则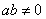 . 假命题 (2) 原命题:若
. 假命题 (2) 原命题:若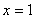 ,则
,则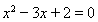 ; 真命题 逆命题:若
; 真命题 逆命题:若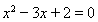 ,则
,则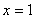 ; 假命题 否命题:若
; 假命题 否命题:若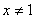 ,则
,则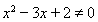 ; 假命题 逆否命题:若
; 假命题 逆否命题:若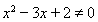 ,则
,则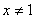 . 真命题 (3) 原命题:若一个三角形有两条边相等,则这个三角形有两个角相等;真命题 逆命题:若一个三角形有两个角相等,则这个三角形有两条边相等;真命题 否命题:若一个三角形没有两条边相等,则这个三角形没有两个角相等;真命题 逆否命题:若一个三角形没有两个角相等,则这个三角形没有两条边相等. 真命题 【总结升华】 ①一般地,先将命题改写成“若…,则…”的形式,再写出其他命题形式;某些命题存在大前提,写其它命题时应注意保留. ②互为逆否命题的两个命题是等价的,同为真或同为假,因此在判定真假时,只需判定二者中的一个. 举一反三: 【变式】写出下列的命题的逆命题,否命题和逆否命题,并判
. 真命题 (3) 原命题:若一个三角形有两条边相等,则这个三角形有两个角相等;真命题 逆命题:若一个三角形有两个角相等,则这个三角形有两条边相等;真命题 否命题:若一个三角形没有两条边相等,则这个三角形没有两个角相等;真命题 逆否命题:若一个三角形没有两个角相等,则这个三角形没有两条边相等. 真命题 【总结升华】 ①一般地,先将命题改写成“若…,则…”的形式,再写出其他命题形式;某些命题存在大前提,写其它命题时应注意保留. ②互为逆否命题的两个命题是等价的,同为真或同为假,因此在判定真假时,只需判定二者中的一个. 举一反三: 【变式】写出下列的命题的逆命题,否命题和逆否命题,并判 断它们的真假. (1)对顶角相等; (2)空集A是非空集合B的真子集; 【答案】 (1) 原命题:如果两角是对顶角,那么这两角相等(真命题); 逆命题:如果两角相等,那么两角是对顶角(假命题); 否命题:如果两角不是
断它们的真假. (1)对顶角相等; (2)空集A是非空集合B的真子集; 【答案】 (1) 原命题:如果两角是对顶角,那么这两角相等(真命题); 逆命题:如果两角相等,那么两角是对顶角(假命题); 否命题:如果两角不是 对顶角,那么这两角不相等(假命题); 逆否命题:如果两
对顶角,那么这两角不相等(假命题); 逆否命题:如果两 角不相等,那么这两角不是对顶角(真命
角不相等,那么这两角不是对顶角(真命 题).[来源:Z*xx*k.Com] (2) 原命题:
题).[来源:Z*xx*k.Com] (2) 原命题: 若A是空集,则A是非空集合
若A是空集,则A是非空集合 B的真子集(真命题); 逆命题:若A是非空集合B的真子集,则A是空集(假命题); 否命题:若A不是空集,则A不是非空集合B
B的真子集(真命题); 逆命题:若A是非空集合B的真子集,则A是空集(假命题); 否命题:若A不是空集,则A不是非空集合B 的真
的真 子集(假命题); 逆否命题:若A不是非空集合B的真子集,则A不是空集(真命题). 例5.设命题: 若
子集(假命题); 逆否命题:若A不是非空集合B的真子集,则A不是空集(真命题). 例5.设命题: 若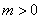 ,则关于
,则关于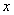 的方程
的方程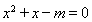 有实数根.试写出它的逆命题,否命题和逆否命题,并分别判断其真假. 【思路点拨】 判断原命题,逆命题,否命题,逆否命题的真假时,只要判断原命题与逆命题的真假,就可知道其它两个命题的真假,不必一一判断. 【解析】 逆命题:若关于
有实数根.试写出它的逆命题,否命题和逆否命题,并分别判断其真假. 【思路点拨】 判断原命题,逆命题,否命题,逆否命题的真假时,只要判断原命题与逆命题的真假,就可知道其它两个命题的真假,不必一一判断. 【解析】 逆命题:若关于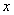 的方程
的方程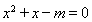 有实数根,则
有实数根,则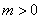 . 否命题:若
. 否命题:若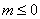 ,则关于
,则关于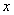 的方程
的方程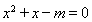 无实数根. 逆否命题:若关于
无实数根. 逆否命题:若关于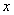 的方程
的方程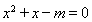 无实数根,则
无实数根,则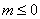 . ①先判断原命题和逆否命题的真假. ∵
. ①先判断原命题和逆否命题的真假. ∵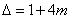 , ∴ 当
, ∴ 当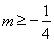 时,方程有实数根. ∵当
时,方程有实数根. ∵当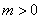 时,
时,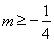 成立,∴ 方程有实数根,∴原命题为真,逆否命题也为真. ②判断逆命题和否命题的真假 当方程有实数根,即
成立,∴ 方程有实数根,∴原命题为真,逆否命题也为真. ②判断逆命题和否命题的真假 当方程有实数根,即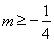 时,推不出
时,推不出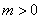 ,∴逆命题为假,否命题也为假. 【总结升华】 先将命题中的条件等价转化,然后关于不等式的集合的命题可以借助于集合的韦恩图解决
,∴逆命题为假,否命题也为假. 【总结升华】 先将命题中的条件等价转化,然后关于不等式的集合的命题可以借助于集合的韦恩图解决 . 举一反三: 【
. 举一反三: 【 变式1】试写出下列命题的逆命题,否命题和逆否命题,并分别判断其真假. (1
变式1】试写出下列命题的逆命题,否命题和逆否命题,并分别判断其真假. (1 )当集合
)当集合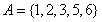 ,
,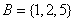 时,若
时,若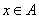 ,则
,则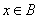 . (2)若
. (2)若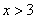 ,则
,则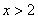 ,
,  (3)若
(3)若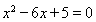 ,则
,则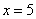 【答案】 (1) 原命题:当集合
【答案】 (1) 原命题:当集合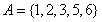 ,
,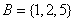 时,
时, 若
若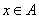 ,则
,则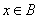 (假命题); 逆命题:当集合
(假命题); 逆命题:当集合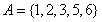 ,
,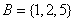 时,若
时,若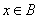 ,则
,则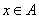 (真命题); 否命题:当集合
(真命题); 否命题:当集合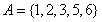 ,
,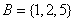 时,若
时,若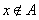 ,则
,则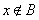 (真命题); 逆否命题:当集合
(真命题); 逆否命题:当集合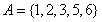 ,
,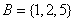 时,若
时,若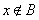 ,则
,则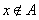 (假命题). (2) 原命题:若
(假命题). (2) 原命题:若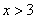 ,则
,则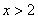 (真命题); 逆命题:若
(真命题); 逆命题:若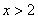 ,则
,则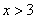 (假命题);[来源:学#科#网] 否命题:若
(假命题);[来源:学#科#网] 否命题:若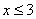 ,则
,则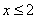 (假命题); 逆否命题:若
(假命题); 逆否命题:若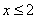 ,则
,则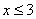 (真命题). (3) 原命题:若
(真命题). (3) 原命题:若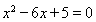 ,则
,则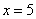 (假命题); 逆命题:若
(假命题); 逆命题:若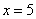 ,则
,则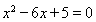 (真命题);
(真命题); 否命题:若
否命题:若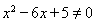 ,则
,则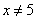 (真命题); 逆否命题:若
(真命题); 逆否命题:若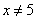 ,则
,则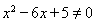 (假命题). 【变式2】已知命题:“如果
(假命题). 【变式2】已知命题:“如果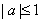 ,那么关于
,那么关于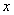 的不等式
的不等式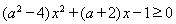 的解集是空集”,写出它的逆命题,否命题,逆否命题,并判断它们的真假. 【答案】 逆命题:如果关于
的解集是空集”,写出它的逆命题,否命题,逆否命题,并判断它们的真假. 【答案】 逆命题:如果关于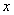 的不等式
的不等式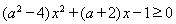 的解集是空集,那么
的解集是空集,那么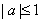 ; 否命题:如果
; 否命题:如果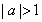 ,那么关于
,那么关于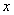 的不等式
的不等式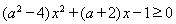 的解集不是空集;
的解集不是空集; 逆否命题:如果关于
逆否命题:如果关于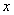 的不等式
的不等式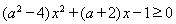 的解集不是空集,那么
的解集不是空集,那么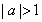 . ① 判断原命题的真假. 当
. ① 判断原命题的真假. 当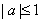 时,
时,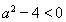 ,
,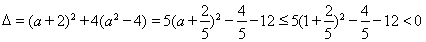 , 故
, 故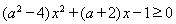 的解集为
的解集为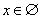 ,故原命题为真,则逆否命题亦真. ② 对于逆命题,当
,故原命题为真,则逆否命题亦真. ② 对于逆命题,当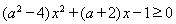 的解为空集时, 先研究
的解为空集时, 先研究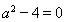 得
得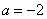 ,满足题意, 这样
,满足题意, 这样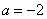 与
与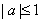 矛盾,故命题为假,而否命题与逆命题互为逆否命题,故否命题亦为假.
矛盾,故命题为假,而否命题与逆命题互为逆否命题,故否命题亦为假.
长按图片点关注,学习数学不迷路!

版权声明:本文为weixin_39747383原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。