堆排序图文详解

基础知识
堆结构是完全二叉树的结构，即从根节点到倒数最二层满足每个根节点都有两个子节点，最后一层可以不完全填充，但是叶子节点必须靠左对齐。在程序中是用数组来表示一个堆，若根节点在数组中的下标为index，则满足以下关系：
左子节点的下标left = 2*index+1，右子节点下标right = 2*index+2；

若当前节点的下标为index，则其父节点的下标为(index-1)/2。

算法整体思路
堆排序（从小到大）主要分为两个部分，建立大根堆和堆调整。建立大根堆即保证堆顶元素为最大值，将堆顶元素（在数组中下标为0）与末尾元素（在数组中下标为len-1）交换，这样数组末尾的元素即为最大值。但此时受到交换的影响，堆顶元素不是最大值，再通过堆调整将剩下的元素调整为大根堆，再将其与数组倒数第二位元素交换。。。以此类推，直到整个数组有序。

建立大根堆步骤
1、对于堆中每个节点，将其与当前根节点比较，若比当前根节点大，则交换

2、将当前根节点作为当前节点，与上层根节点继续上述比较，直到与整个堆的根节点比完为止

3、以数组【2 1 4 0 8 10 3】为例，建立大根堆的步骤如下图：

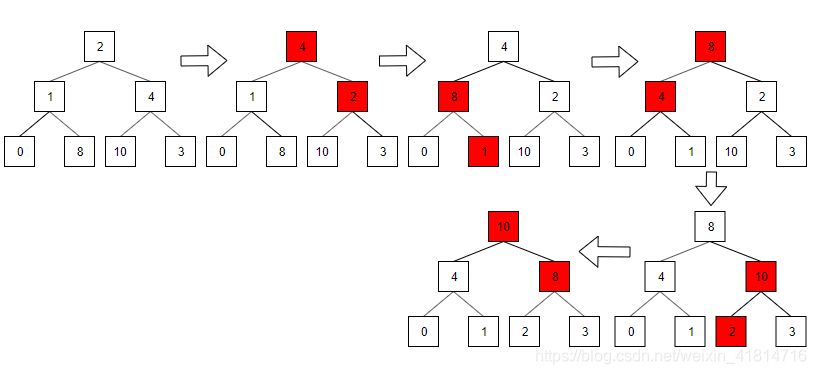
堆调整
1、从整个堆的根节点开始，取其左右子节点值较大的与根节点值比较，若比根节点值大，则交换

2、再将较大值作为当前节点，重复步骤1操作，直至当前节点下标到达堆末尾为止

3、上述数据的堆调整的步骤如下

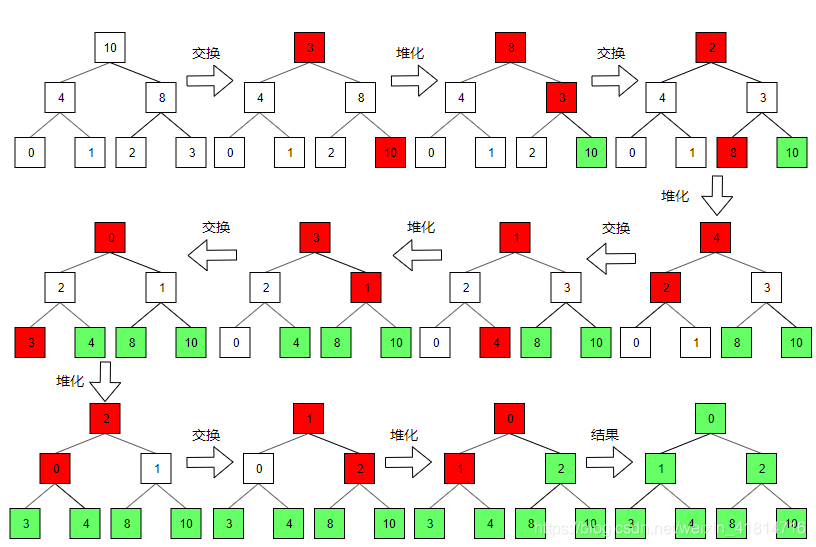
Java代码
经上述操作后，数组即为有序，Java代码如下

public static void heapSort(int[] arr) {
		if(arr == null || arr.length < 2)
			return;
		for(int i = 0; i < arr.length; i++) {
			heapInsert(arr, i);//插入一个新的值建立大根堆
		}
		int heapSize = arr.length;
		swap(arr, 0, --heapSize);//将堆顶位置放在数组末尾
		while(heapSize > 0) {
			heapify(arr, 0, heapSize);//将剩下的位置调整为大根堆
			swap(arr, 0, --heapSize);
		}	
	}
	//插入新的结点，建立大根堆时间复杂度O(N)
	public static void heapInsert(int[] arr, int index) {
		while(arr[index] > arr[(index - 1) / 2]) {//若当前位置比父位置大则交换
			swap(arr, index, (index-1)/2);
			index = (index-1)/2;//将根节点作为当前结点继续比较，直到与整颗数的根节点比较完为止
		}	
	}
	//若大根堆某个数变小，则与子节点比较，沉底O(logN)
	public static void heapify(int[] arr, int index, int heapSize) {
		int left = index * 2 + 1;
		while(left < heapSize) {
			int largest = left + 1 < heapSize && arr[left+1] > arr[left]
					? left + 1
				    : left;//选择左右子节点值大的那个
			largest = arr[largest] > arr[index] ? largest : index;//根节点与子节点较大的比较
			if(largest == index)
				break;
			swap(arr, largest, index);//若子节点值较大，将该子节点与根节点交换
			index = largest;//更新根节点
			left = index * 2 + 1;//取根节点左子节点继续上述操作
		}	
	}