算法实现步骤
给定一个增广的训练模式集{y1,y2,⋅⋅⋅,yN},其中每个模式类别已知,它们分别属于w1类,w2类:
- 给定初步数始值K=0,令增量ρ=C,(C为正常数),给定初始增广权矢量W(0)赋任意小的值;
- 输入训练模式yK,计算判别函数值:W(K)T∗yK;
校正增广权矢量,校正规则是:
若yK∈w1和W(K)T∗yK≤0则:W(K+1)=W(K)+ρ∗yK;
若yK∈w2和W(K)T∗yK≥0则:W(K+1)=W(K)−ρ∗yK;
否则不需校正即:W(K+1)=W(K).若w2类各个分量乘(−1),则校正规则为:
W(K)T∗yK≤0则:W(K+1)=W(K)+ρ∗yK;令K=K+1,继续第二步,直到W对所有的样本均稳定不变,即对样本进行正确分类结束。
Matlab代码实现
clear all;
close all;
clc;
%给定样本:
%w1 = (x1,x2) = {(0,0),(0,1)}
%w2 =(x3,x4)= {(1,0),(1,1)}
x1 = [0,0];x2 = [0,1];x3 = [1,0];x4 = [1,1];
%增广型训练模式集
y1 = [x1,1];y2 = [x2,1];y3 = [-x3,-1];y4 = [-x4,-1];
y = [y1;y2;y3;y4];
%给定初始权矢量,增量,步数
W = [1;1;1]; P = 1; K = 0;
d = zeros(4,2000);%用来存储判别函数
for i = 1:2000
for j = 1:4
K = K + 1;
d(j,i) = y(j,:)*W;
if d(j,i) <= 0
W = W + y(j,:)';%当d<=0,需校正;d>0,不校正
end
end
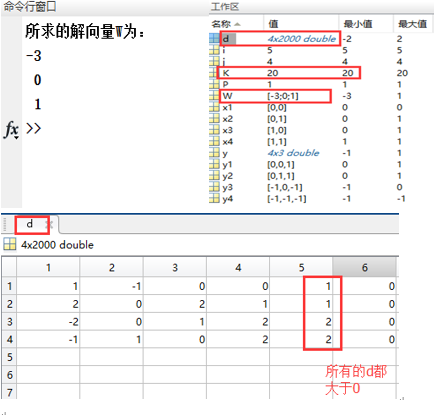
if d(:,i)>0 %迭代到所有训练样本的判别函数大于0时,结束迭代,输出解向量
disp( '所求的解向量W为:');
disp( num2str(W));
break
end
end结果图
版权声明:本文为liuzhuomei0911原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。