本文资料全部来源互联网，仅作为笔记使用

RoI Pooling - 2015

为什么需要RoI Pooling？

我们回顾一下R-CNN中，ROI的产生：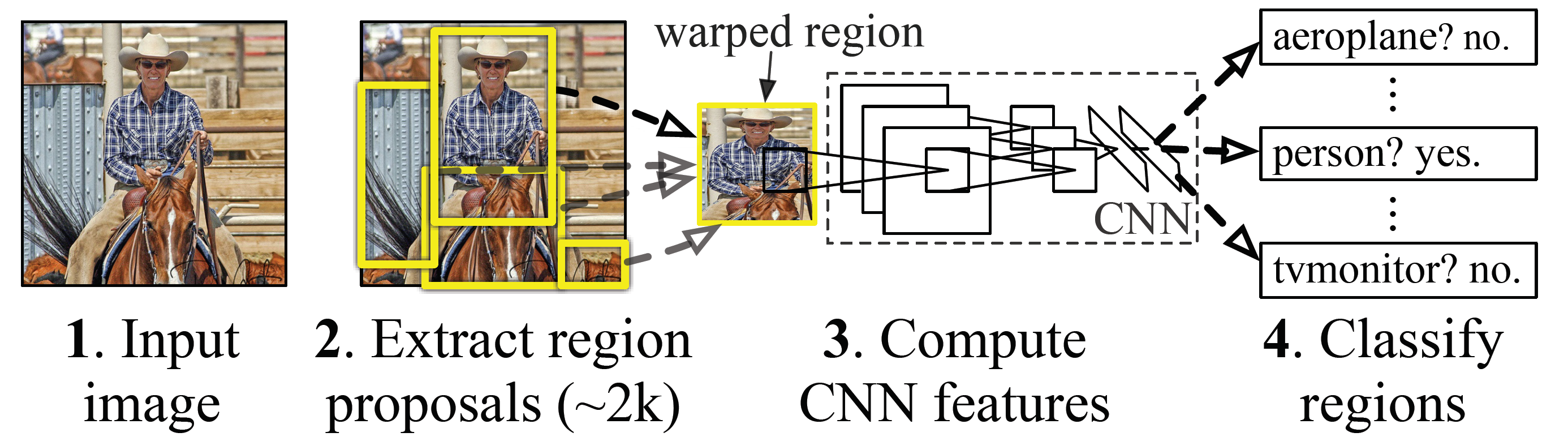
在这里插入图片描述
在原图上选取proposal，然后warp成固定大小，其实就是做resize。再送入卷积层，此时的输出相当于Fast R-CNN中ROI Pooling的输出。

为什么需要RoI Pooling？其根本原因是为了解决R-CNN中每个proposal都需卷积的问题。而RoI Pooling的使用是为了处理在feature map上选proposal与full connected layer尺寸不一样问题。

2015年，Fast R-CNN借鉴SPPnet中的SPP，一层的SPP就是RoI Pooling

下面以Fast R-CNN为例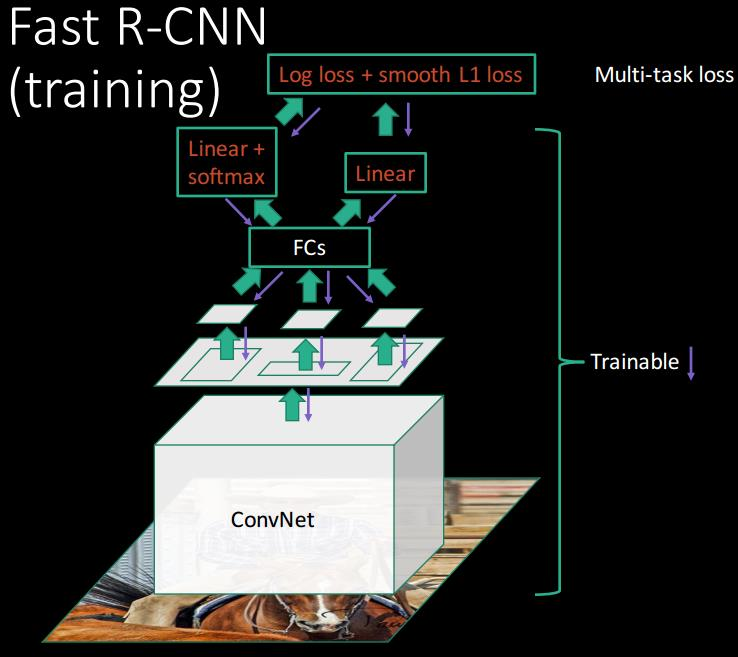
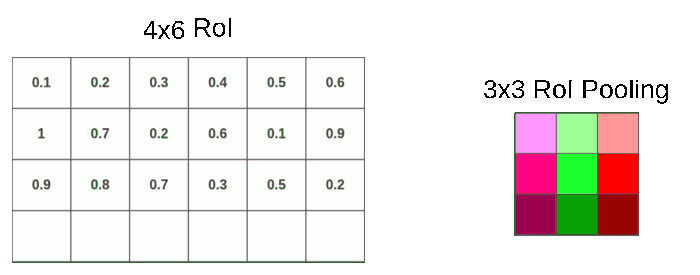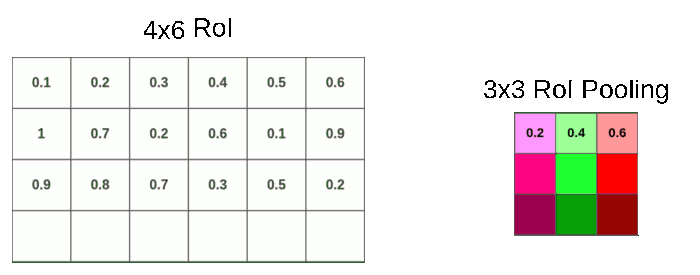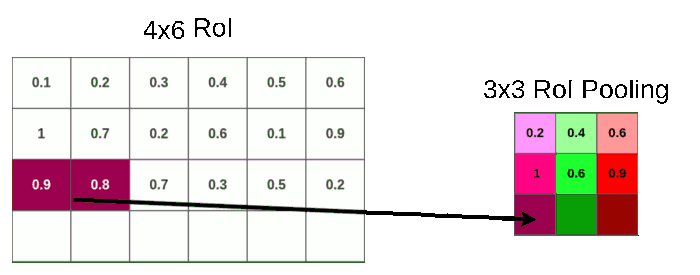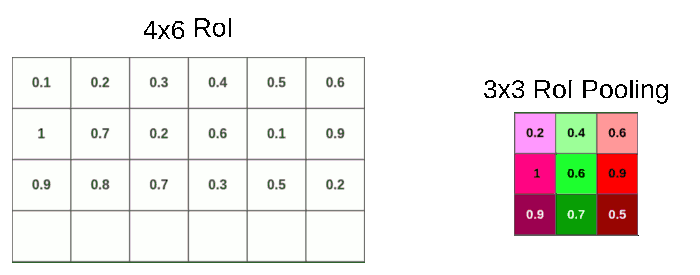
在这里插入图片描述
可以看到先对原图进行卷积，得到卷积层，在将Selective Search选择的proposals对应到卷积层。由于proposal尺寸不一样，需要进行RoI pooling。比如最后的共享卷积层后，有一个proposal：

以下图片来自这里，非常棒的一篇可视化介绍文章。

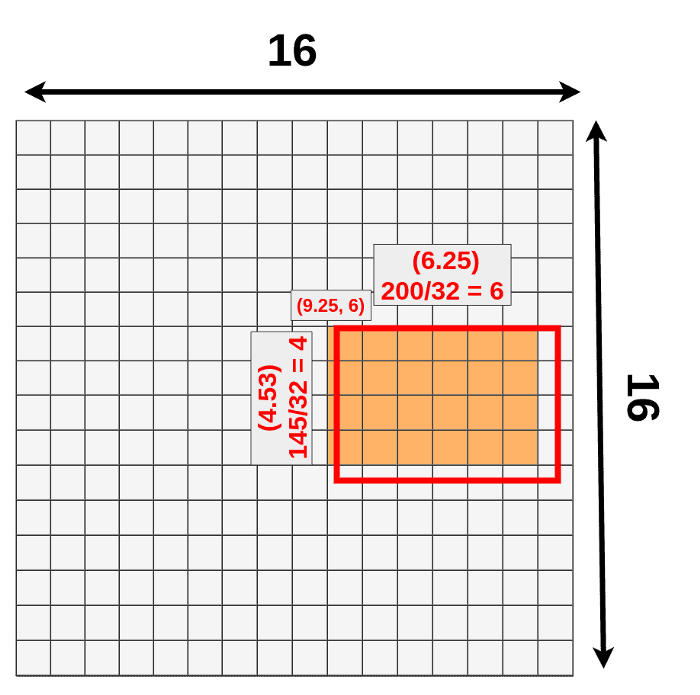
在这里插入图片描述
我们知道左上角坐标和长，宽，映射到feature map时，有小数进行四舍五入，这是第一次量化。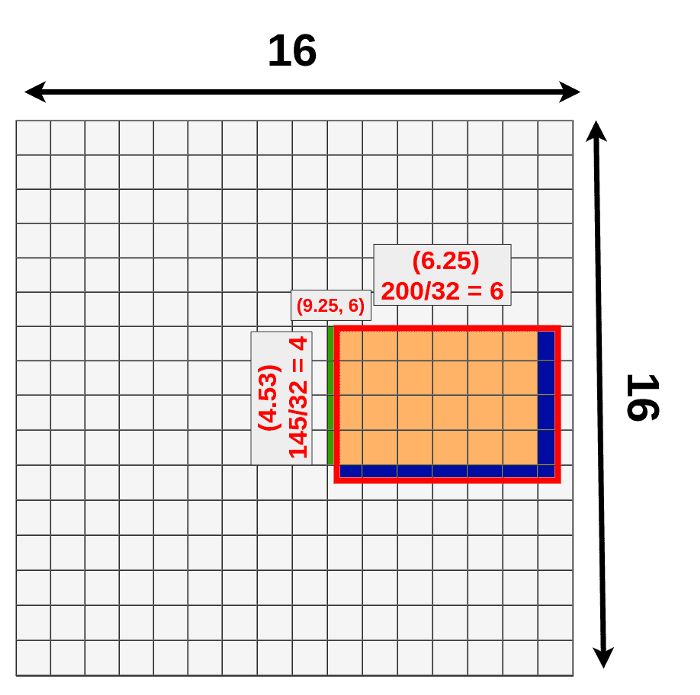

第一次量化带来的不准确地方：

丢失蓝色部分
额外绿色部分

进行RoI Pooling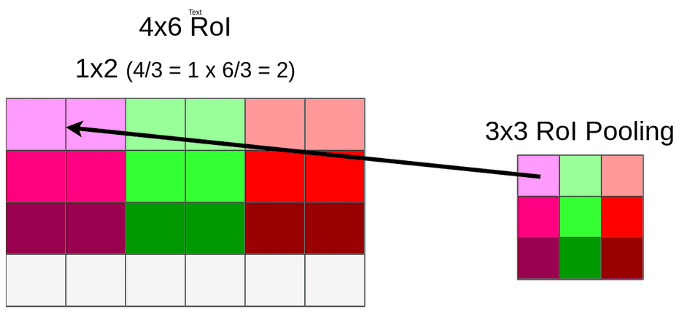
在这里插入图片描述
假设RoI Pooling的输出是固定的为 $9 * 9$ ，那么就要对这个特征图进行划分，那么划分出来的每一块的大小就是 $4 / 3 * 6 / 3 = 1.3 * 2$ ，进行第二次量化也是进行取整变成 $1 * 2$ 。

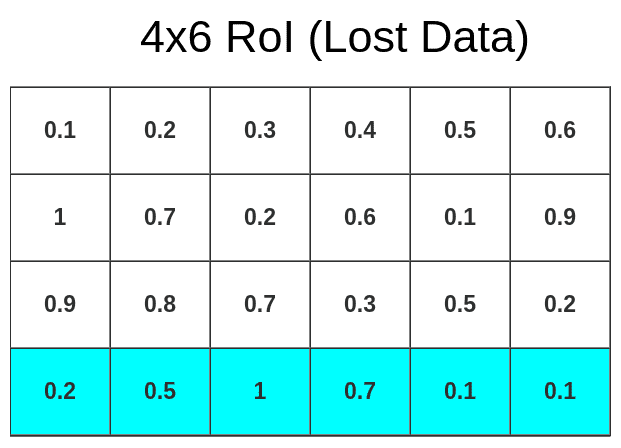
在这里插入图片描述
第二次量化再次带来数据缺失。

在这里插入图片描述

2次量化带来的不精确：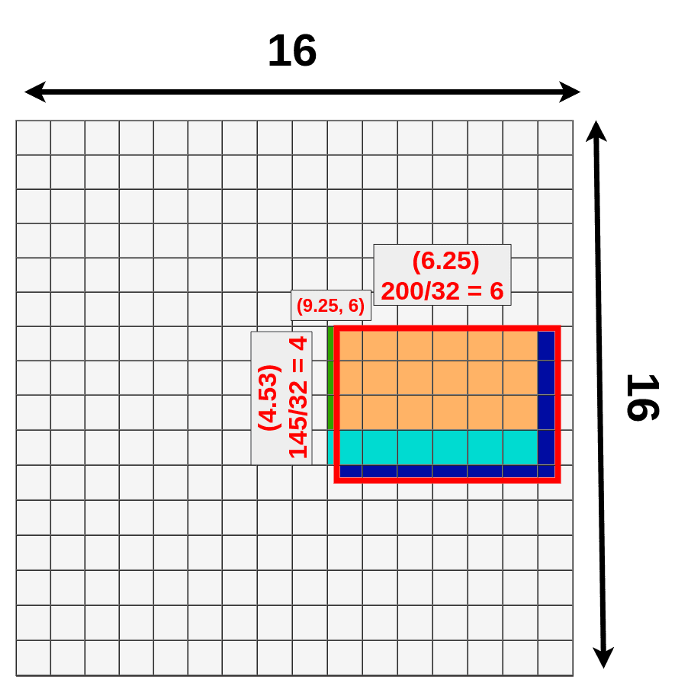
在这里插入图片描述

和SPP对比，就是只有一层（尺度）的SPP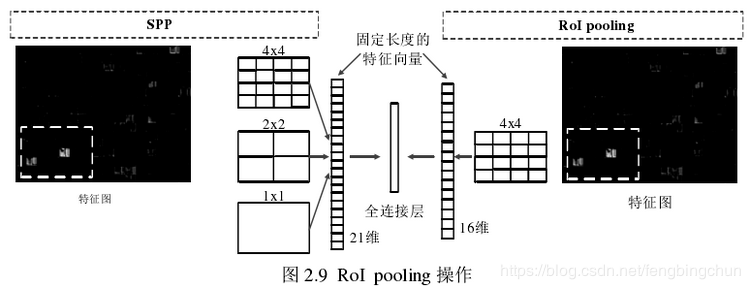
在这里插入图片描述

Back-propagation through RoI Pooling layers

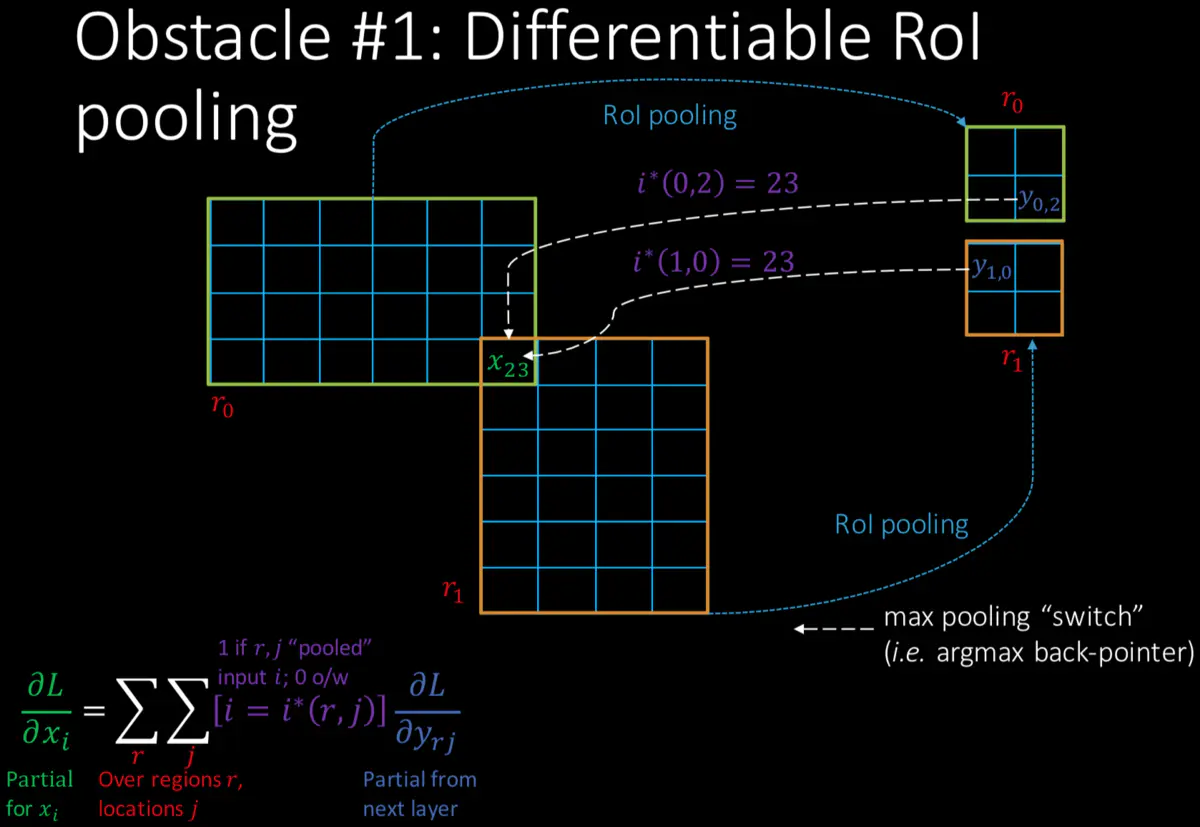
在这里插入图片描述
在ROI层反向传播，对每个proposals的网格做如下判断， $x_i$ 中的i是否对应当前ROI，换句话说就是 $i=i^{*}(r,j)]$ 表示特征图上的第i节点是否被候选区域r的第j个节点选为最大值输出。如果是就累加下一个proposals，这样就求出 $\frac{\partial L}{\partial x_{i}}$

ROI Warping pooling - 2015

ROI Warping pooling的想法和RoI Align差不多，唯一的区别是ROI Warping pooling是将RoI量化到feature map上。

1.corp操作：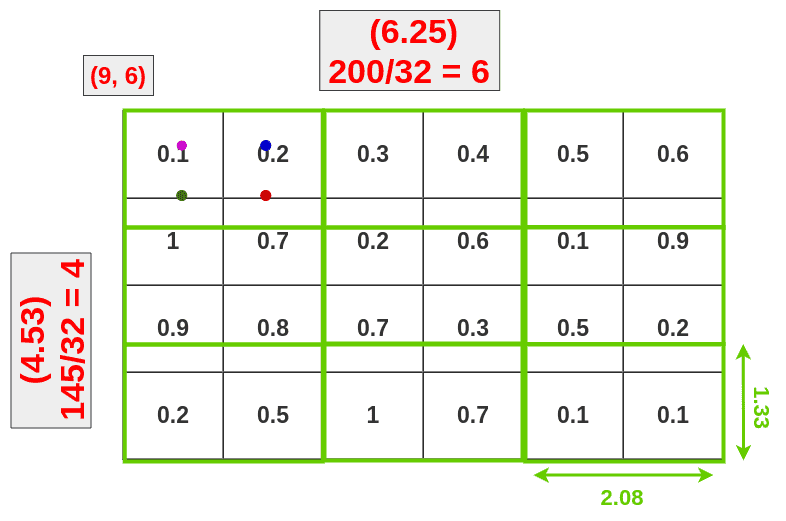
在这里插入图片描述
可以看到，在feature map 上执行了第一次量化（取整）

2.warp操作:
与RoI Pooling不一样但是和后面提到的RoI Align一样。不在进行第二次量化而是进行双线性插值，

数据损失和补充图：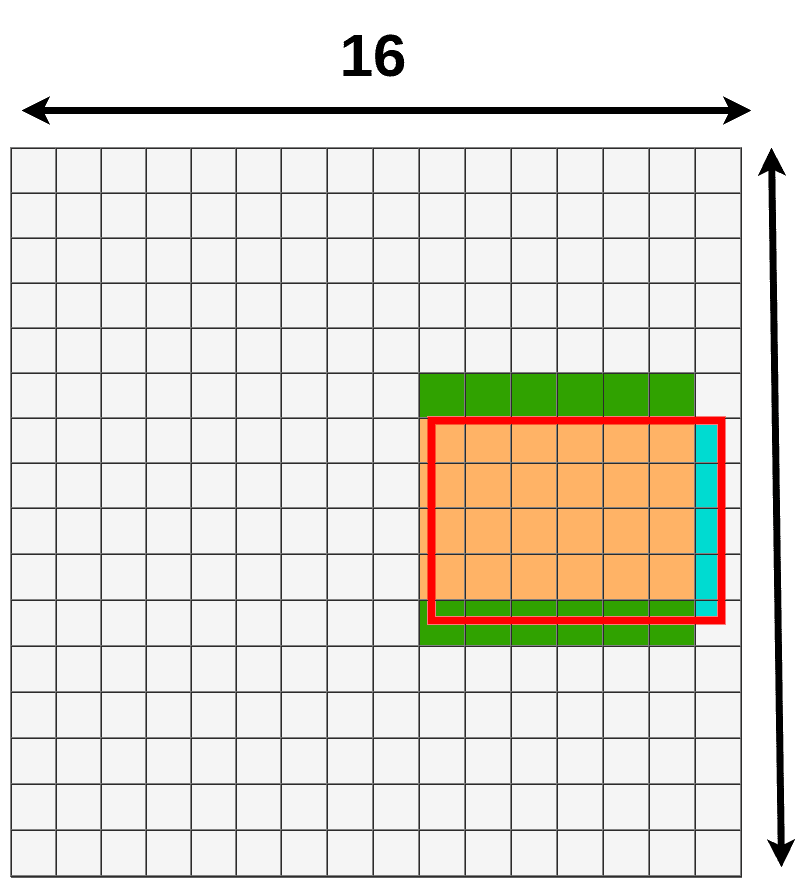
在这里插入图片描述
关于绿色部分：双线性插值需要从周围取部分数据，距离越近，取得越多。

PS-ROI Pooling - 2016

为什么需要PS-ROI Pooling？

这个问题其实是问为什么需要R-FCN：

引入位置敏感，卷积可以保持位置信息，但是经过全连接后，位置信息不再保留，这也是为什么CNN分类器在分类上可以做的很好，但是在检测上效果不好。Fast/er R-CNN类的方法在ROI pooling前都是卷积，但一旦插入ROI pooling之后，后面的网络结构就不再保留位置信息。
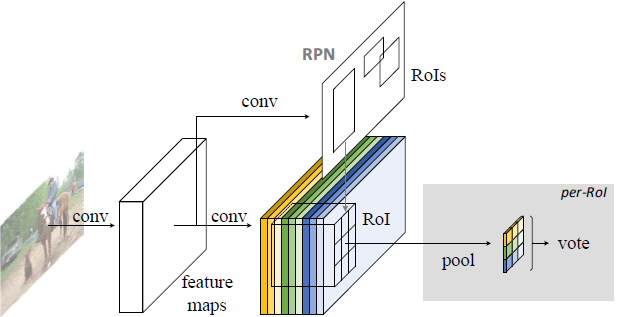
对于region-based的检测方法，以Faster R-CNN为例，实际上是分成了几个subnetwork，第一个用来在整张图上做比较耗时的conv，这些操作与region无关，是计算共享的。第二个subnetwork是用来产生候选的boundingbox（如RPN），第三个subnetwork用来分类或进一步对box进行regression（如Fast RCNN），这个subnetwork和region是有关系的，必须每个region单独跑网络，衔接在这个subnetwork和前两个subnetwork中间的就是ROI pooling。我们希望的是，耗时的卷积都尽量移到前面共享的subnetwork上。因此，和Faster RCNN中用的ResNet（前91层共享，插入ROI pooling，后10层不共享）策略不同，R-FCN把所有的101层都放在了前面共享的subnetwork。最后用来prediction的卷积只有1层，大大减少了计算量。

为了实现位置敏感就提出PS-ROI Pooling，核心思想是position sensitive score map。
把位置信息以层的形式就组成position sensitive score maps，进行一次卷积就计算了多个ROI的最终输出(固定长度)。

在这里插入图片描述

这里有必要提一下为什么 fully connected layer会去除目标的位置信息。参考这一篇文章。

全连接层是怎么操作？
它是怎么样把3x3x5的输出，转换成1x4096的形式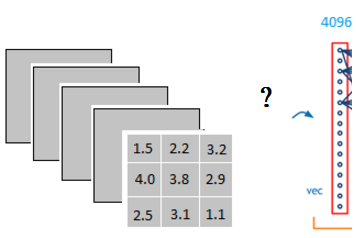
在这里插入图片描述
很简单,可以理解为在中间做了一个卷积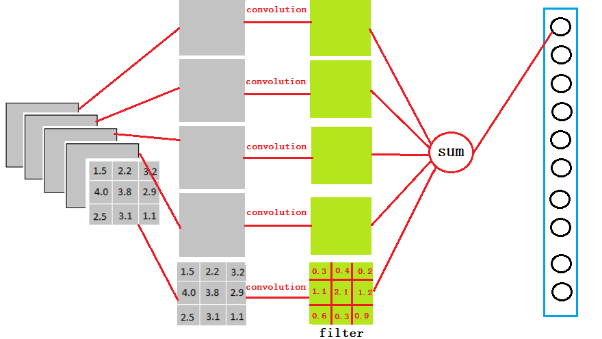

从上图我们可以看出，我们用一个3x3x5的filter 去卷积激活函数的输出，得到的结果就是一个fully connected layer 的一个神经元的输出，这个输出就是一个值，因为我们有4096个神经元，我们实际就是用一个3x3x5x4096的卷积层去卷积激活函数的输出。3 *3 代表 feature map 大小，当然会有更大的size，比如 7 * 7。
全连接层作用？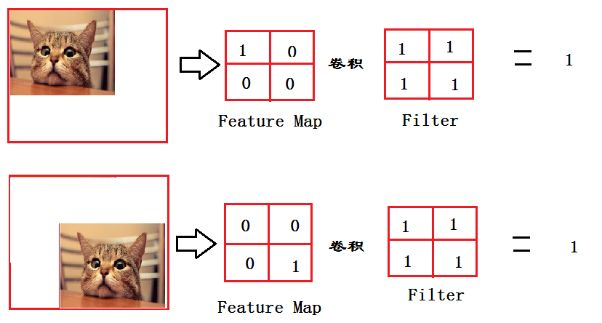
在这里插入图片描述
从上图我们可以看出，猫在不同的位置，输出的feature值相同。因为空间结构特性被忽略了，所以全连接层不适合用于在方位上找Pattern的任务，比如segmentation。
有人会说，bbox位置确定在Fast-RCNN中是在另外一个分支进行回归，没有这个问题，但是可以看下面R-FCN结构图，只有一个分支，所以是不能使用fully connected layer。而是利用了全局平均池化来进行输出。

全连接层参数特多（可占整个网络参数80%左右），近期一些性能优异的网络模型如ResNet和GoogLeNet等均用全局平均池化（global average pooling，GAP）取代全连接层来融合学到的深度特征，需要指出的是，用GAP替代FC的网络通常有较好的预测性能。

2016年，R-FCN中提出了PS-ROI Pooling，参考详细的R-FCN讲解

计算步骤

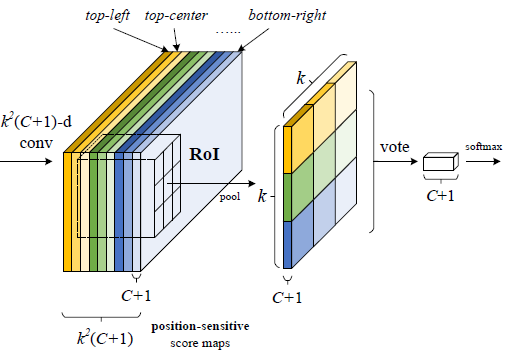
在这里插入图片描述

PS-ROI Pooling更像一个框架，有多个步骤。

输入是ROI features, 输出是C+1维的特征向量。

首先，在ROI层的上一层，指定其需要经过 $k^2(C+1)$ 维的 $1 * 1$ 卷积， $w*h*k^2(C+1)$ 大小的作为ROI输入。这里， $k^2$ 代表一个ROI里所有矩形单元的数量，比如 $k = 3$ 也就是上左（左上角），上中，上右，中左，中中，中右，下左，下中，下右（右下角）共9个子区域， $C + 1$ 代表所有的类别数加上背景。这 $k^2*(C+1)$ 张特征图每 $C + 1$ 张分成一组、共包含 $k^2$ 组，每组负责向对应的子区域进行响应。
然后，进行PS-ROI Pooling，得到 $k^2*(C+1)$ 的ROI输出。池化每一个ROI时，各个点（一共 $k^2$ 个），均由上一层中对应分组的对应位置区域内通过平均池化获得。由此获得一组 $C + 1$ 张大小为 $k^2$ 投票矩阵。
最后，每个类对应有9个位置的投票值，这9个值求和，就是这个类的概率。

在这里插入图片描述
为和框架图对应，改成这种形式：

如果ROI偏离目标，最后投票得分会降低：

在这里插入图片描述
最后解释一下公式：
$r_{c}(i, j \mid \Theta)=\sum_{(x, y) \in \operatorname{bin}(i, j)} z_{i, j, c}\left(x+x_{0}, y+y_{0} \mid \Theta\right) / n$

共有k*k = 9个颜色，每个颜色的立体块 $W * H * (C + 1)$ 表示的是不同位置存在目标的概率值（第一块黄色表示的是左上角位置，最后一块淡蓝色表示的是右下角位置）。共有 $k^2*(C+1)$ 个feature map。每个feature map， $z (i, j, c)$ 是第 $i + k (j - 1)$ 个立体块上的第c个map（ $1 < = i, j < = 3$ ）。(i,j)决定了9种位置的某一种位置，假设为左上角位置（i=j=1），c决定了哪一类，假设为person类。在 $z (i, j, c)$ 这个feature map上的某一个像素的位置是（x,y），像素值是value，则value表示的是原图对应的(x,y)这个位置上可能是人（c=‘person’）且是人的左上部位（i=j=1）的概率值。除n就是平均池化操作，和ROI pooling一样。

以k=7, C=20为例，具体的数据形式如下：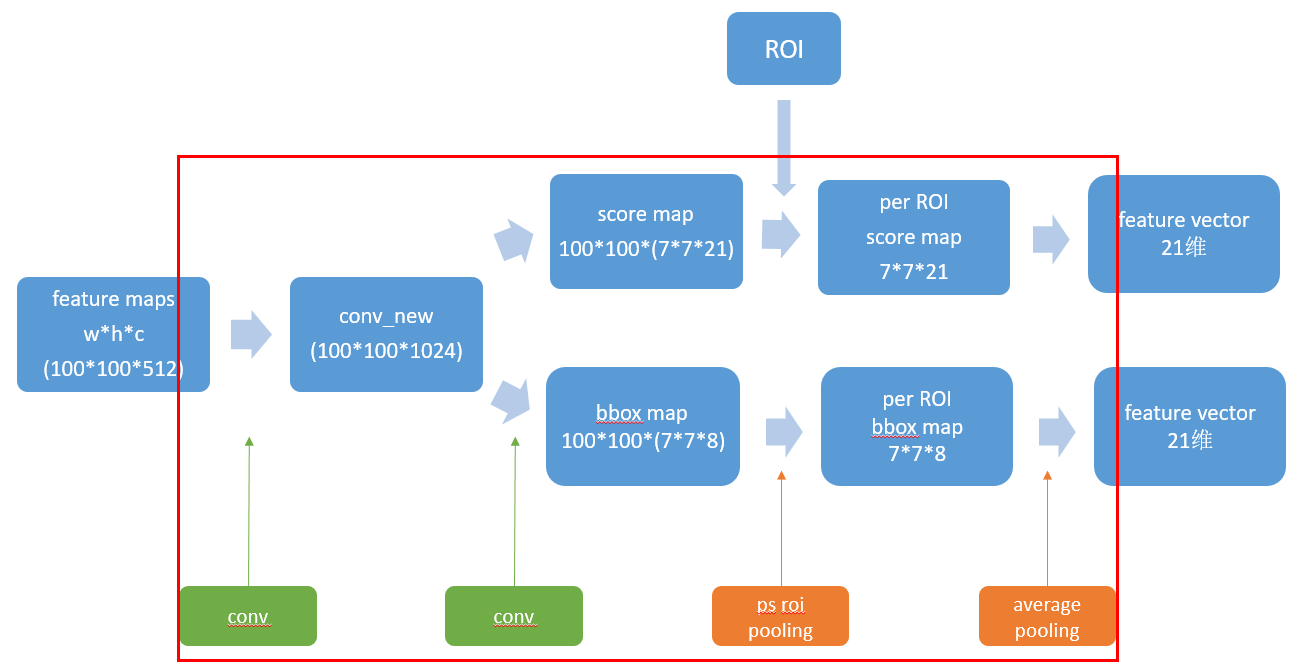
在这里插入图片描述
其实在第二个卷积的时候，它产生的 $7 * 7 * 21$ 个输出，是不知道具体所谓的位置信息的，而是后面的position-sensitive roi pooling这一步的特定选取规则，使得对于每一类，这49个maps产生了差异，在训练的时候，为了使最后的损失函数最小，这49输出对应的kernel就慢慢地显现出差异。

rfcn的核心是延续fastRCNN的思想：对于每一个proposal，所有的卷积操作（费时的操作）都只做一次。fastRCNN提出baseNet，让proposal从feature map上寻找roi，但是不同的proposal还是得重复进行后面的全连接层；rfcn提出psROIpooling, 让proposal从bbox map和score map上寻找roi，从而取消全连接层，这样不同的proposal做的重复的事情，就只有后面的average pooling。其实，per roi map还是二维的，最后二维变成一维是通过average pooling来实现的。

示例图如下：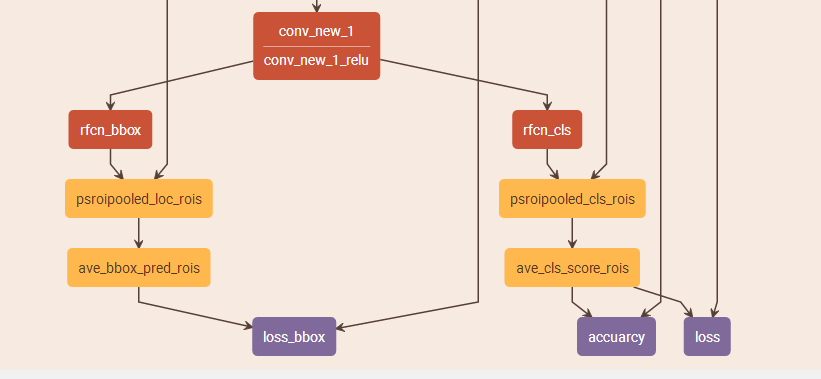
在这里插入图片描述

计算反向传播时，遵循“向对应位置回传梯度的原则”，池化后的每一个点回传的梯度传向池化前特征图上对应通道对应区域的特征点上。具体实现可参见源码：PSROI-Pooling 源码

RoI Align - 2018

为什么需要ROI Align？

从上面可以发现，虽然经过RoI Pooling转换后得到的长度一样了，然后可以接全连接层。
但是存在以下问题：
region proposal的xywh通常是小数，但是为了方便操作会把它整数化。
将整数化后的边界区域平均分割成 k x k 个单元，对每一个单元的边界进行整数化。
两次整数化的过程如下图所示：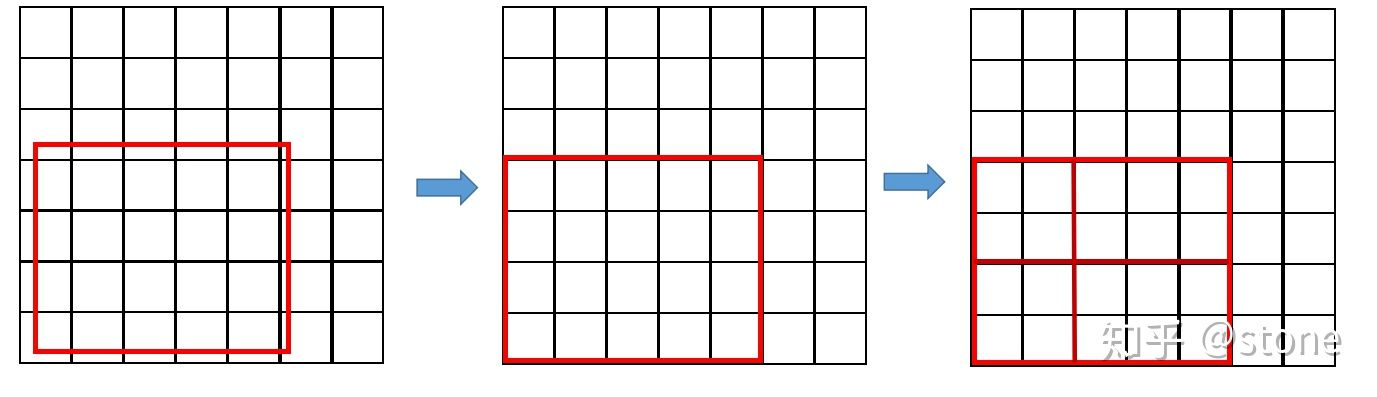
在这里插入图片描述
事实上，经过上述两次整数化，此时的候选框已经和最开始回归出来的位置有一定的偏差，这个偏差会影响检测或者分割的准确度。在论文里，作者把它总结为“不匹配问题”（misalignment）。而mask检测，即实例分割（instance segmentation）需要像素-Feature Map对应，所以就有下面的RoI Align。

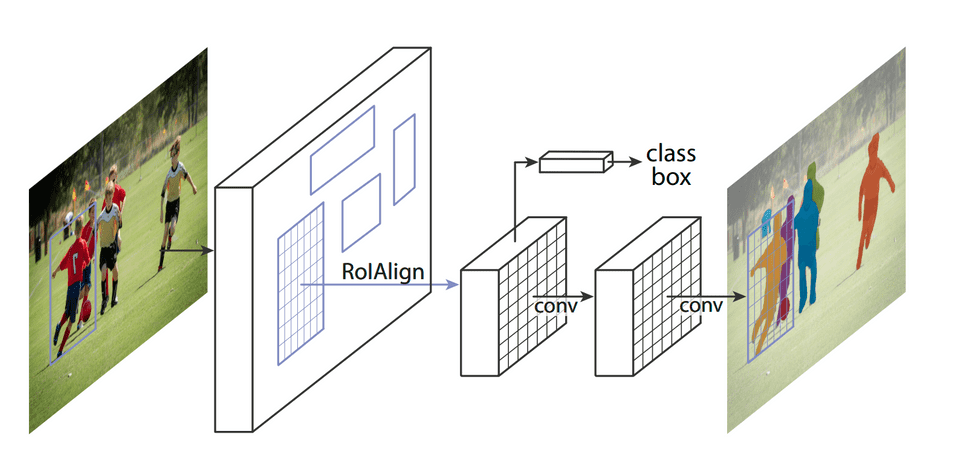
在这里插入图片描述
在2018年，Mask R-CNN中提出RoI Align。

比如ROI(proposal)是黑框，蓝色虚线交点处是Featur Map的点，下面把ROI分成2 * 2网格，这一步和RoI Polling一样

接下来对每个网格取4个采样点（RoI Polling是根据网格划分的结果中去对应的Featur Map，由于进行了整数化，就不存在小数），4个采样点没有进行取整，所以进行双线性插值，双线性插值核心思想就是那个点举例采样点近，那个点发挥的作用就更大。

最后的步骤也和RoI Polling一样，网格内的采样点取一个最大值代表这个网格。所以最后输出的结果是固定大小。
在这里插入图片描述

需要说明的是，在相关实验中，作者发现将采样点设为4会获得最佳性能，但是直接设为1在性能上也相差无几。事实上，ROI Align 在遍历取样点的数量上没有ROIPooling那么多，但却可以获得更好的性能，这主要归功于解决了misalignment的问题。

具体计算步骤：

以下图片来自这里，非常棒的一篇可视化介绍文章。

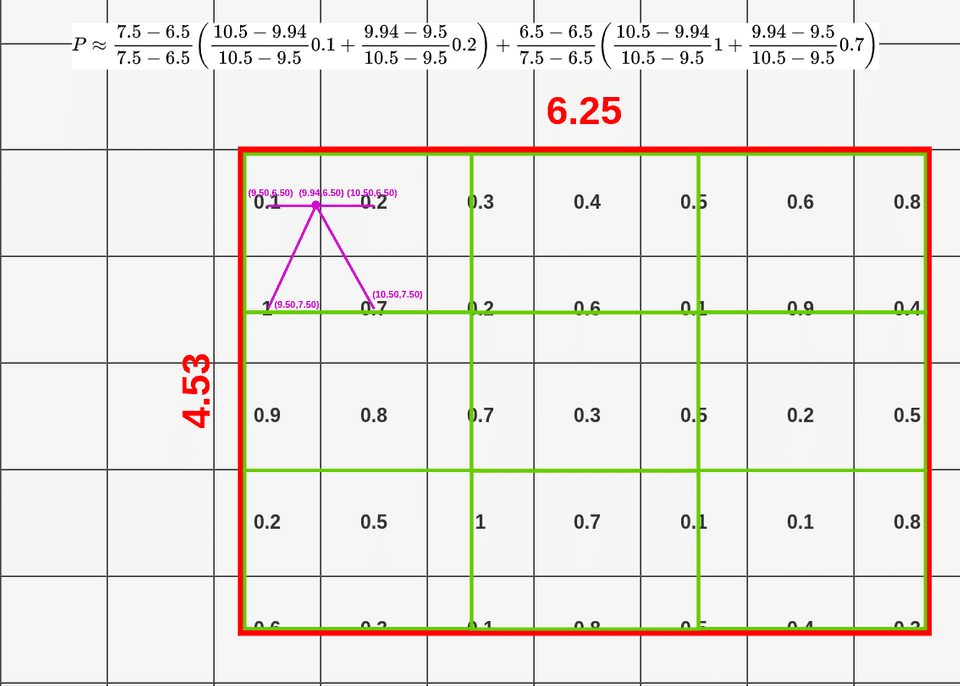
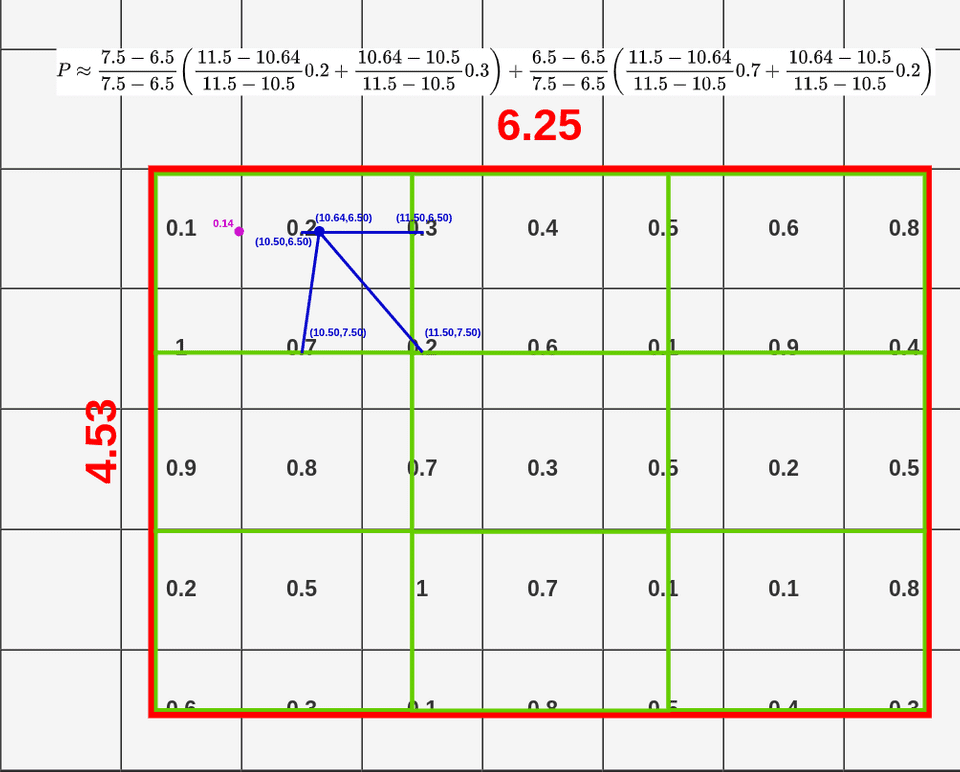
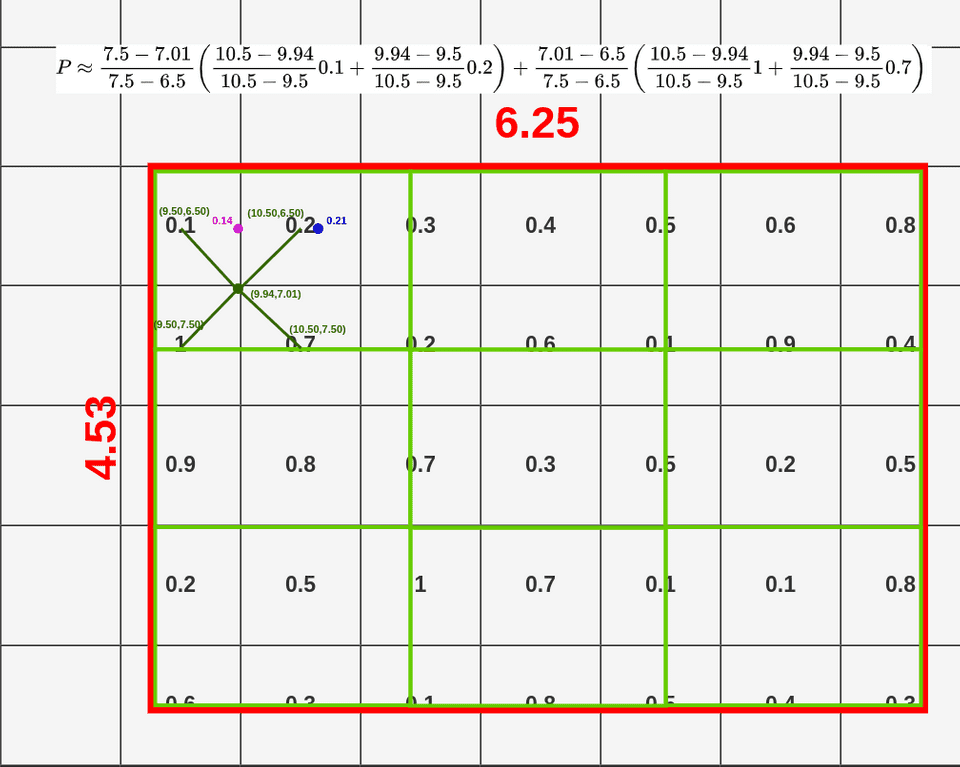
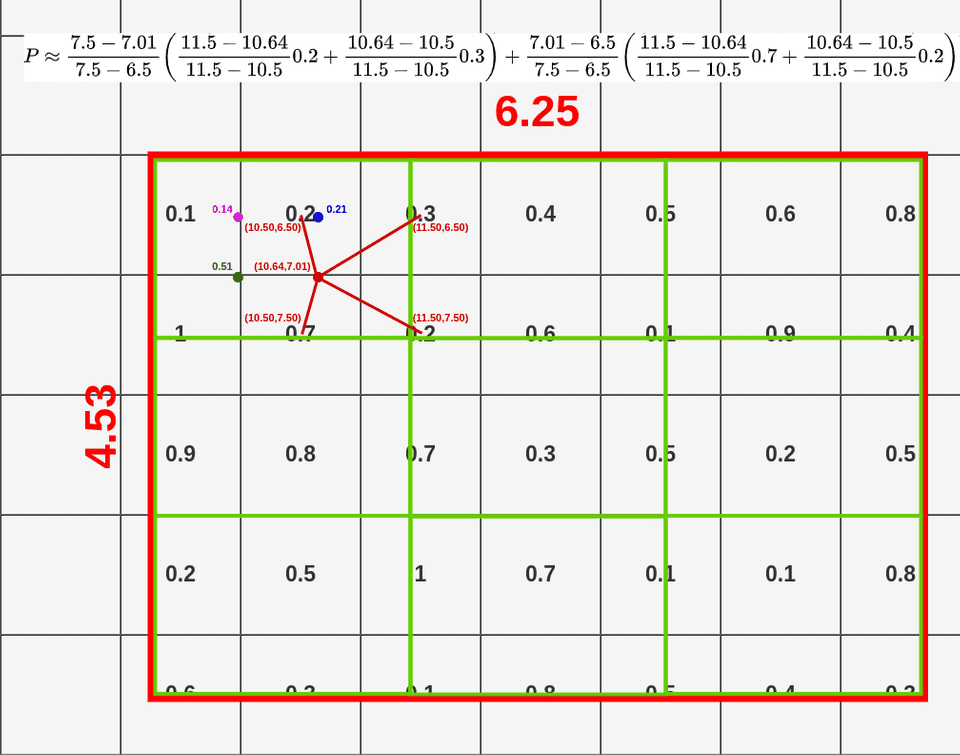
在这里插入图片描述

RoIAlign 和 RoIPooling 数据来源对比：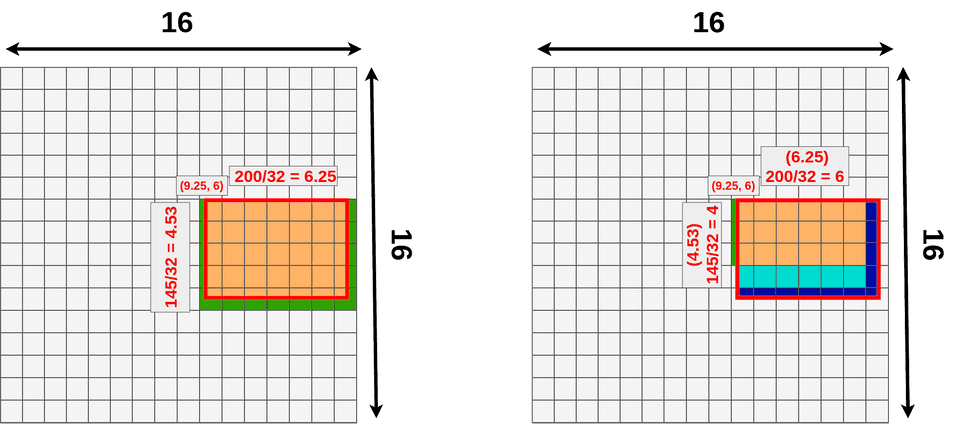
在这里插入图片描述
绿色表示ROI区域额外信息
蓝色(第一次量化)和天蓝色(第二次量化)表示丢失信息

Back-propagation through RoI Align layers

和ROI Pooling核心思想是一样的，但是在ROI Align中， $i^*(r,j)$ 是一个浮点数的坐标位置(前向传播时计算出来的采样点)，在池化前的特征图中，每一个与 $i^*(r,j)$ 横纵坐标均小于1的点都应该接受与此对应的点 $y_{rj}$ 回传的梯度，故ROI Align 的反向传播公式如下:

$\frac{\partial L}{\partial x_{i}}=\sum_{r} \sum_{j}\left[d\left(i, i^{*}(r, j)\right)<1\right](1-\Delta h)(1-\Delta w) \frac{\partial L}{\partial y_{r j}}$
上式中， $d (.)$ 表示两点之间的距离， $Δ h$ 和 $Δ w$ 表示 $i$ 与 $i^*(r,j)$ 横纵坐标的差值，这里作为双线性内插的系数乘在原始的梯度上。

PS-ROI Align

将 ROI Align 移植到 PS-ROI Pooling 中，实现了一个 Position Sensitive ROI Align 的算法。主要改进就是两次量化的取消：ROI的边界坐标值和每个ROI中所有矩形单元的边界值保持浮点数形式，在每个矩形单元中计算出固定位置固定数量的采样点的像素值作平均池化。具体的前向传播和反向传播细节如下：

前向传播：
a. 遍历池化后特征图上的每一个像素点，在池化前特征图上寻找对应通道上的对应区域；
b. 将每一个候选区域平均划分成 n * n 个单元；
c. 在每一个单元内，按照设置的采样点数目计算出采样点的坐标值；
d. 使用双线性内插的方法计算出特征图上每一个采样点处所对应的值；
e. 依照平均池化的方式计算出 a 步骤中当前点的值，并且记录下所有采样点的位置坐标。
反向传播：
a. 遍历池化后特征图上的每一个像素点，在池化前特征图上寻找对应通道上的对应区域；
b. 在a步骤的当前区域中遍历每一个点，分别和前向传播中记录下来的所有采样点坐标比较，如果横纵坐标都小于1，则回传平均后的梯度值。
初步的实验表明，PS-ROI Align 对模型的检测性能有提升，对小物体的感知能力有明显改善。PSROIAlign源码

PrROI Pooling - 2018

为什么需要PrROI Pooling？动机？

RoI Align取消两次2量化，feature map通过双线性插值表示成连续的特征图，用函数 $f$ 表示连续的特征图，用 $w$ 表示离散的特征图，于是有：

$y)=\sum_{i, j} I C(x, y, i, j) \times w_{i, j}$

其中， $j)=\max (0,1-|x-i|) \times \max (0,1-|y-j|)$ 是插值系数，体现了连续点 $(x, y)$ 和离散点 $(i, j)$ 距离越大，插值系数越小。

那么既然可以连续表示，而RoI Align在一个区域bin内需要确定采样点，比如上面是取4，再做平均。我们可以这样理解，我们就是需要取bin内平均值。

具体步骤：
现在我们为某个Rol指定它的一个bin, bin $=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right)\right\},$ 其中 $\left(x_{1}, y_{1}\right)$ 和 $\left(x_{2}, y_{2}\right)$ 分别表示矩形框的左上角和右下角坐标，如下图所示（当然，这个坐标值是连续数值，因为已经做过插值了）：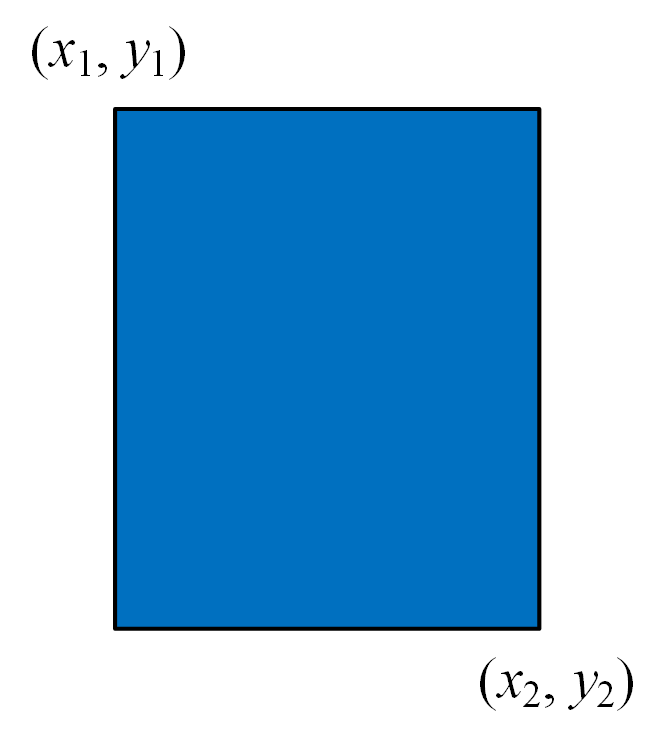
在这里插入图片描述
根据上述得到的bin（其坐标是连续数值）和原始的特征图 $\mathcal{F}$ ，我们可以进行一种pooling操作，它涉及到二重积分：
$\operatorname{PrPool}(\operatorname{bin}, \mathcal{F})=\frac{\int_{y 1}^{y / 2} \int_{x 1}^{x 2} f(x, y) d x d y}{\left(x_{2}-x_{1}\right) \times\left(y_{2}-y_{1}\right)}$
从上面的公式可以看出，PrPool的主要计算思想是对bin区域内的数值进行求和，然后除以bin的面积。或者说是体积处于底面积，算平均高度，这个高度就是平均值。

最后进行对比：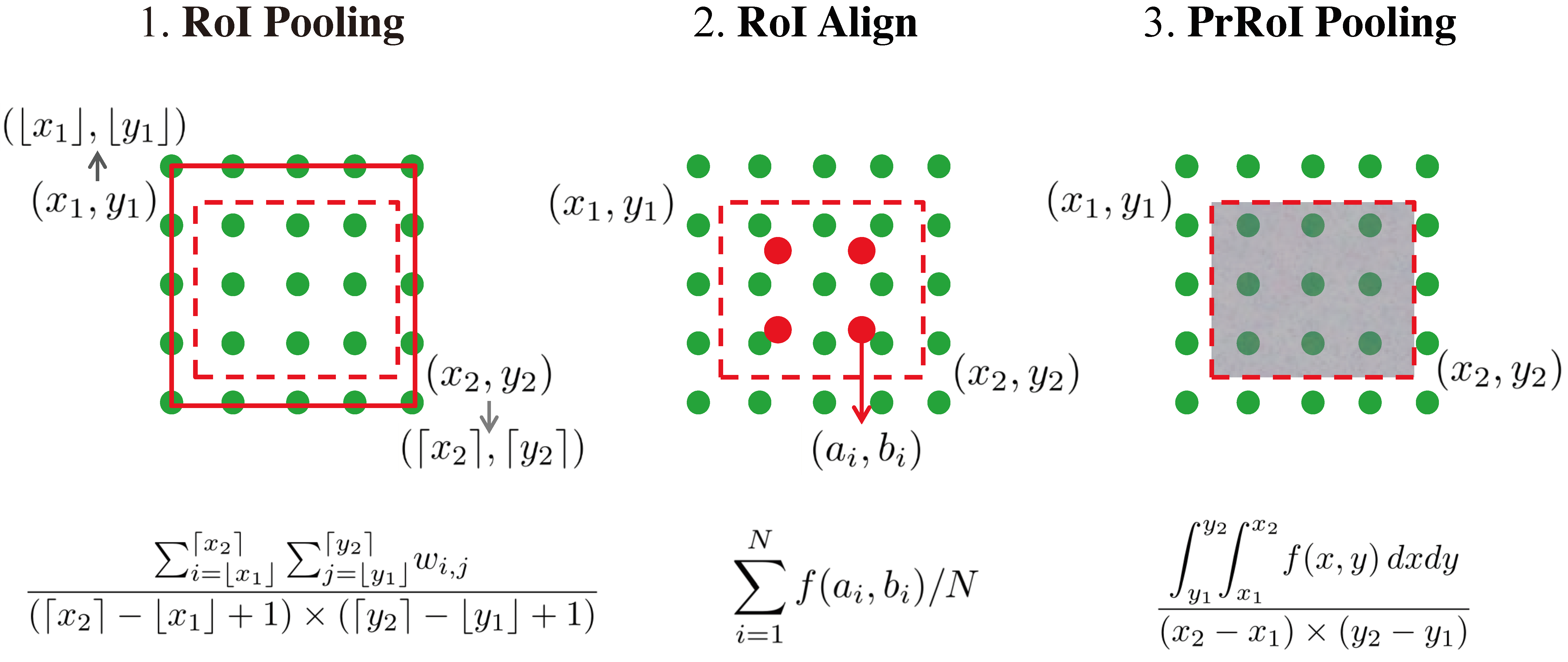
在这里插入图片描述
上图中红色虚线表示候选图像在特征图中的位置。从图中可以看出，RoI Pooling的思路最为基础，其方法是直接做了取整处理，损失了精度。RoI Align方法则首先进行插值，然后将候选图像区域分为若干个子区域（图中的示例是4个子区域，表现为4个实心红点），最后pooling的时候对这4个子区域做均值处理。与RoI Align方法类似，PrRoI Pooling也做了插值处理，将离散的特征图数据映射到一个连续空间，但与RoI Align不同之处在于，它并没有再划分子区域，而是使用二重积分再求均值的方式实现pooling。相比于RoI Align方法，PrRoI Pooling主要解决了N的取值难以自适应的问题。

总结：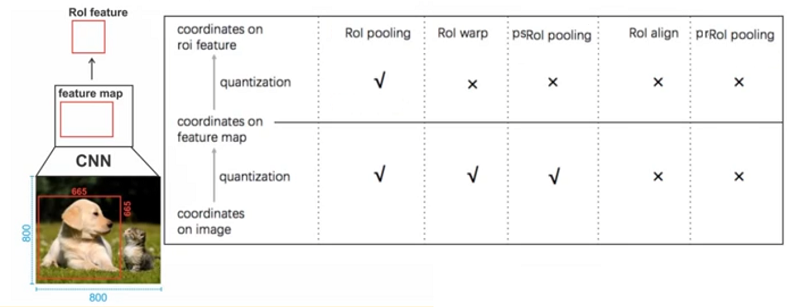
在这里插入图片描述

参考

原文链接：https://blog.csdn.net/qq_29598161/article/details/108137399