单调栈数据结构

顾名思义，单调栈就是说栈中的元素是单调的，递增或者递减。一般来说，解决问题用的单调栈存放的都是原数组元素的索引。

单调栈的构造：

对于一个非单调的数据序列arr，如何构造单调递增栈：

stack = []
for a in arr:
	if not stack or stack[-1]<=a:# 如果栈空，或者元素比栈中最后一个元素大，则入栈
		stack.append(a)
	else: # 如果栈非空，且元素比栈中最后一个元素小，则删除栈所有比该元素大的元素，以保证单调递增
		while stack and stack[-1]>a:
			stack.pop()
		stack.append(a) # 删除所有比a大的元素后，a入栈

应用一：找到每个元素后面比它大的第一个数

题目描述：给定一个无序数组，找到每个元素后面比它大的第一个数
分析：给定一个数组例如7 5 3 2 1 4，我们对其建立单调栈，我们希望每拿来一个新元素，如果该元素比栈头元素大，则作为结果输出，因此我们使用单调递减栈。由于栈单调递减，因此遇到一个新元素时，该元素会作为栈中所有比它小的元素的输出结果，如图：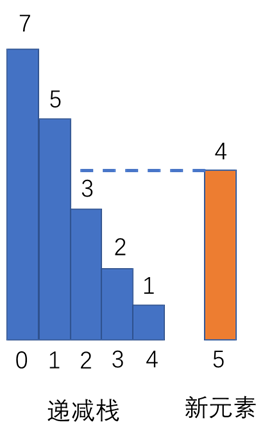
注意，单调栈中存放的是各元素在原数组中的索引

#include <iostream>
#include <vector>
#include <stack>

using namespace std;
class Solution {
public:
    vector<int> find_first_bigger_one(vector<int>& vec) {
        stack<int> stk;
        vector<int> res(vec.size(), 0);
        for (int i=0; i<vec.size(); ++i) {
            while(!stk.empty() && vec[i] > vec[stk.top()]) {
            	// 记录的是第一个比它大的数的数值
                res[stk.top()] = vec[i];
                stk.pop();
            }
            stk.push(i);
        }
        // 对于栈中剩余的元素，他们的右边没有比他们更大的数了，所以赋值为-1
        while (!stk.empty()) {
            res[stk.top()] = -1;
            stk.pop();
        }
        return res;

    }
};

int main() {
    Solution sol;
    vector<int> vec = {7,5,3,2,1,4};
    vector<int> result = sol.find_first_bigger_one(vec);
    for (auto a:result){
        cout<<a <<" ";
    }
    cout<<endl;
}

应用二：视野问题

题目描述：给定一个数组，对于每一个数，找到其和右边比他大的第一个数之间的间隔。（一群高度不完全相同的牛从左到右站成一排，每头牛只能看见它右边的比它矮的牛的发型，若遇到一头高度大于或等于它的牛，则无法继续看到这头牛和后面的其他牛的发型。给出这些牛的高度，要求每头牛可以看到的牛的数量的和。）
分析：和应用一其实属于同一问题，区别就是找到第一个比当前数大的数之后，记录间隔而不是记录那个数；

#include <iostream>
#include <vector>
#include <stack>

using namespace std;
class Solution {
public:
    vector<int> find_first_bigger_one(vector<int>& vec) {
        stack<int> stk;
        vector<int> res(vec.size(), 0);
        for (int i=0; i<vec.size(); ++i) {
            while(!stk.empty() && vec[i] > vec[stk.top()]) {
            	// 记录间隔
                res[stk.top()] = i - stk.top() - 1;
                stk.pop();
            }
            stk.push(i);
        }
        // 对于找不到比自己大的元素，使用列表长度减去他们的索引，就得到了他们能看到的个数
        while (!stk.empty()) {
            res[stk.top()] = vec.size() - stk.top() -1;
            stk.pop();
        }
        return res;

    }
};

int main() {
    Solution sol;
    vector<int> vec = {7,5,3,2,1,4};
    vector<int> result = sol.find_first_bigger_one(vec);
    for (auto a:result){
        cout<<a <<" ";
    }
    cout<<endl;
}

应用三：接水问题

问题描述：给定一个直方图(也称柱状图)，假设有人从上面源源不断地倒水，最后直方图能存多少水量?直方图的宽度为 1。
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的直方图，在这种情况下，可以接 6 个单位的水（蓝色部分表示水）。
分析：
1. 什么时候可以接到水？出现凹槽的时候！如果构造一个单调递减栈（至少包含两个元素），则当新元素大于栈顶元素时，就一定会出现凹槽！
2. 凹槽的面积（接水的面积）如何计算？如果按照竖向计算（对水槽进行竖向分割），需要知道栈中所有元素的信息，才能知道计算出水位的高度，从而计算面积，但是对于栈，每次只能知道栈顶元素的信息，因此采用横向计算（对水槽进行横向分割）的方法。当第 $i$ 个新元素大于栈顶元素时（栈中至少有两个元素），设栈顶元素为bottom（水底）左侧元素为left（一定大于bottom），此时水面高度取决于left和新元素的大小，所以计算公式为：
  $v o l = (m i n (h e i g h t [l e f t], h e i g h t [i]) - h e i g h t [b o t t o m]) * (i - l e f t - 1)$

class Solution {
public:
    int trap(vector<int>& height) {
        stack<int> stk;
        stk.push(0);
        int i = 1;
        int res = 0;
        while (i < height.size()) {
            while (!stk.empty() && height[i] > height[stk.top()]) {
                int bottom = stk.top();
                stk.pop();
                if (stk.empty()) {
                    break; // 当bottom出栈后，栈为空，则跳出循环。
                }
                res += (min(height[stk.top()], height[i]) - height[bottom]) * (i - stk.top() -1);
                
            }
            stk.push(i);
            i++;
        }
        return res;
    }
};

这里要注意如何处理栈中至少有两个元素，当bottom出栈后，栈为空，则跳出循环。
也可以分情况讨论：

class Solution {
public:
    int trap(vector<int>& height) {
        stack<int> stk;
        stk.push(0);
        int i = 1;
        int res = 0;
        while (i < height.size()) {
            if (height[i] > height[stk.top()] && stk.size() < 2) {
                stk.pop();
                stk.push(i);
                i++;
            } else if (height[i] > height[stk.top()] && stk.size() >= 2) {
                int bottom = height[stk.top()];
                stk.pop();
                res += (min(height[stk.top()], height[i]) - bottom) * (i - stk.top() -1);
            } else if (height[i] <= height[stk.top()]) {
                stk.push(i);
                i++;
            }
        }
        return res;
    }
};

可以看出这种方法只使用了一层循环。

总结：

单调栈一般在建立的过程中，会同时进行入栈和出栈操作，因此直接记录原数组中的元素没有意义，必须记录原数组中元素的索引！
单调栈在建立过程中，一般包括两层循环，第一层负责遍历原数组，将元素索引入栈；第二层负责判断当出现非单调的情况时，遍历那些影响单调性的元素，将他们出栈，并做后续处理。

原文链接：https://blog.csdn.net/qq_36013249/article/details/105706730