二分查找:
int BinarySearch(int* arr, int size, int to_find) {
assert(arr);
int left = 0;
int right = size - 1;
while (left <= right) {
int mid = (left + right) / 2;
if (arr[mid] < to_find) {
left = mid + 1;
}
else if (arr[mid] > to_find) {
right = mid - 1;
}
else {
return mid;
}
}
return -1;
}
时间复杂度为:O(logN)
求解过程: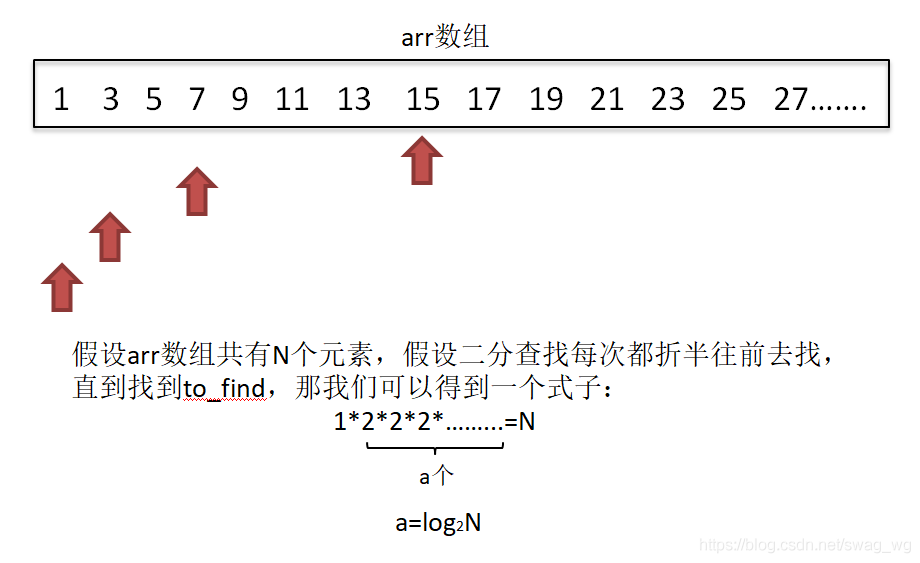
ps: logN在算法分析中表示是底数为2 ,对数为N,有些地方会写成lgN。
递归求阶乘:
long long Factorial(size_t N) {
if (N ==0) {
return 1;
}
return N*Factorial(N - 1);
}
时间复杂度为:O(N)
求解过程:
递归斐波那契:
long long Fibonacci(size_t N) {
if (N < 3) {
return 1;
}
return Fibonacci(N - 1) + Fibonacci(N - 2);
}
时间复杂度为:O(2^N)
求解过程: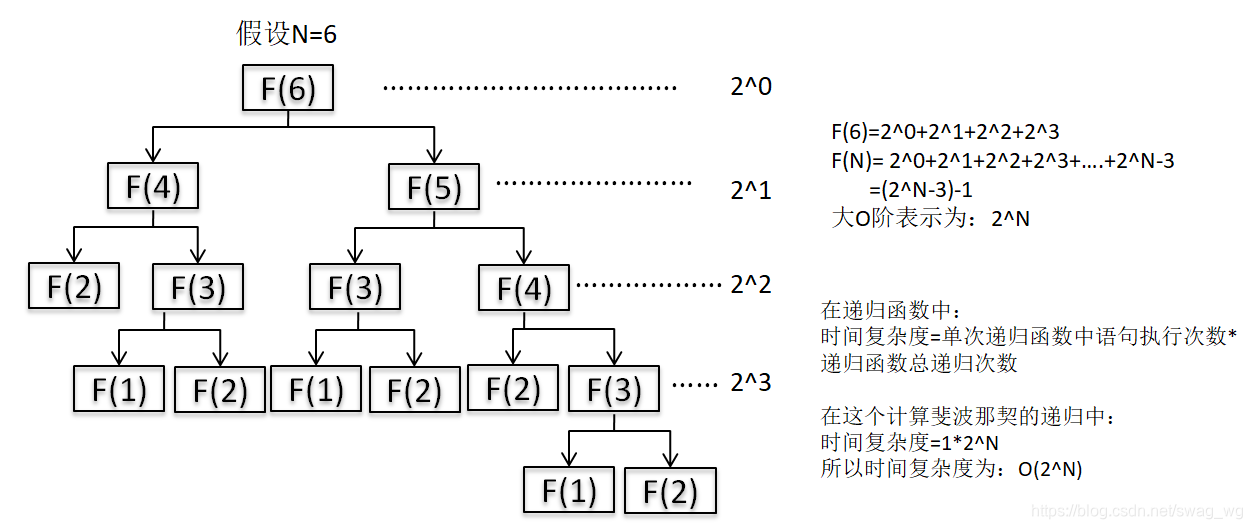
版权声明:本文为swag_wg原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。