今天的文章聊聊高等数学当中的极限,我们跳过极限定义以及一些常用极限计算的部分。我想对于一些比较常用的函数以及数列的极限,大家应该都非常熟悉。
大部分比较简单的函数或者数列,我们可以很直观地看出来它们的极限。比如1/n,当n趋向于无穷大的时候,1/n 的极限是0,再比如当n趋向于无穷大的时候,n的平方的极限也是无穷大,等等。
但是对于一些相对比较复杂的函数,我们一时之间可能很难直观地看出极限,因此需要比较方便计算极限的方法,今天的文章介绍的正是这样的方法——夹逼法和换元法。
夹逼法在数学领域其实非常常用,在中学的竞赛当中经常出现。夹逼法的原理非常简单:
对于某一个函数f(x),我们知道它的表达式,但是很难确定它的范围。我们可以先找到另外两个范围比较容易确定的函数g(x)和h(x),然后证明:
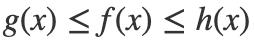
通过h(x)和g(x)的范围来夹逼f(x)的范围。
说白了,就是直接求解不方便的函数,我们通过用其他容易计算的函数来替代的方法来间接求解,类似于“曲线救国”。
明白了夹逼法的概念之后,我们再来看一下它在数列极限当中的应用。
假设当下存在数列 {xn}我们需要确定它的极限,我们找到了另外两个数列 {yn} 和 {zn}。如果它们满足以下两个条件:
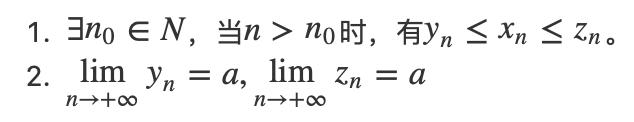
那么,数列 {xn} 的极限存在,并且:
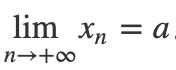
从直觉上来看,上面的式子应该非常直观,但是我们还是试着从数学的角度来证明一下,顺便回顾一下极限的定义。
证明过程如下:
根据极限的定义,对于数列 {xn} 而言,对于任意ϵ都存在 n0 > 0,使得对于任意:n > n0,都有:
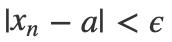
那么就称数列 {xn} 的极限是a。
由于数列 {yn} 的极限是a,所以存在 n1 使得 n > n1 时:
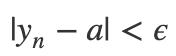
同理,存在 n2 使得 n > n2时:
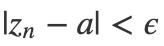
那么对于 n > max(n1, n2)显然应该有:
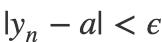
并且
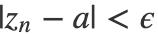
我们将绝对值展开,可以得到:
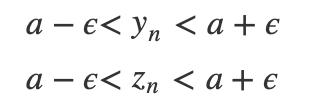
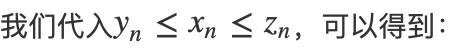
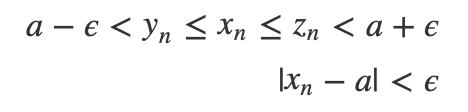
根据极限的定义,显然可以得到数列 {xn} 的极限也是a。
我们利用这个方法来看一个书上的例子:
我们都知道当x趋向于0的时候,x和sinx都趋向于0,但是 sinx/x 的极限是多少呢?如果猜测一下,两个无穷趋向于0的极限的比值应该是1才对,但是这个只是我们的直观猜测,想要严格证明,还需要使用数学方法。
这个证明就用到了我们刚才说的夹逼法,并且非常巧妙,让我们来看一张下面这张图。
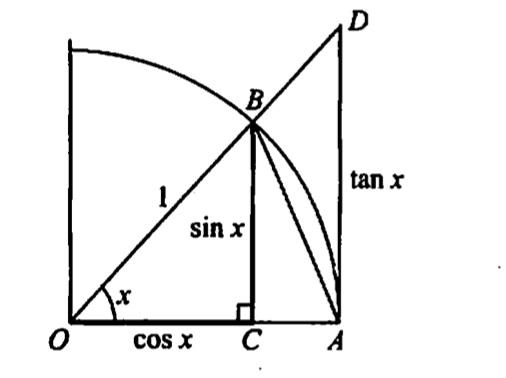
我们假设夹角∠AOB=x,这里采用弧度制。我们令圆心OB的长度等于1,那么BC=sinx,OC=cosx,AD=tanx。我们下面要用这张图里的三角形面积关系,显然:
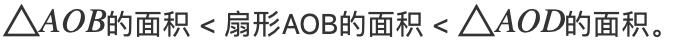
三角形AOB的面积等于 1/2 * OA * BC = 1/2 sinx,三角形AOD的面积等于 1/2 * OA * AD = 1/2 tanx。
这两个都很容易得出,直接套用三角形面积公式即可。扇形的面积看起来麻烦一些,但其实也很简单,在几何当中,扇形可以看成是特殊的三角形。我们把弧长看成是底面,半径可以看成是高,那么扇形的面积等于1/2*弧长*半径。所以扇形AOB的面积等于 1/2 * x * 1 = x/2。
我们列出来,可以得到:
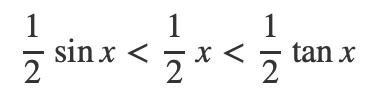
即:
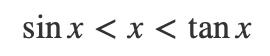
其中
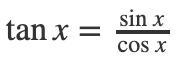
所以我们可以不等号两边同时除以sinx,得到:
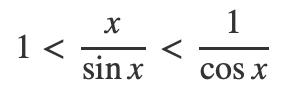
由于当x趋向于0的时候sinx, cosx都大于0,所以我们可以对不等式互换分子分母,得到:
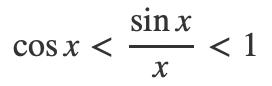
到这里已经结束了,因为我们根据余弦的函数图像可以很容易看出来,当x趋向于0的时候,cosx趋向于1.但为了严谨起见,我们当做不知道这点,继续用数学的方法证明:
我们来计算当x趋向于0的时候,1−cosx的取值范围,当x趋向于0的时候cosx<1,所以1−cosx>0。我们再对1−cosx变形,这里要引入三角函数当中的和差化积公式:
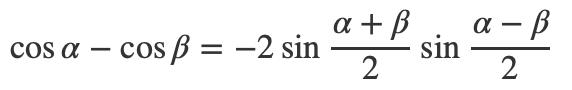
由于cos0=1,带入和差化积可以得到:
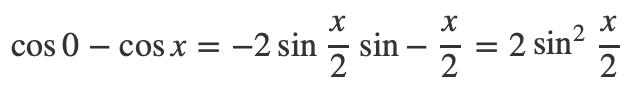
我们之前通过面积表示的方法已经证明了当x趋向于0的时候sinx
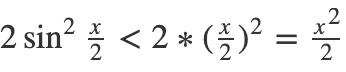
当x趋向于0的时候,显然x^2也趋向于0,所以我们可以证明 cosx 的极限是1。
我们接着来看换元法,在书里被称为复合函数的极限运算法则。假设我们有y=f[g(x)],我们令u=g(x)。如果
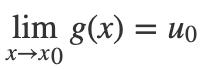
并且
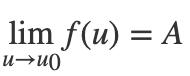
并且在x趋向于x0时,有g(x)≠u0,那么:
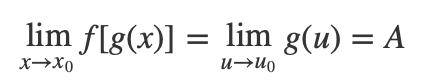
我们使用极限的定义同样可以很方便地证明它的正确性,这里就不证明了,感兴趣的同学可以试着证明一下。
了解了符合函数的极限运算法则之后,我们再来看一个例子巩固一下。
和上面的例子类似,我们这次求一下:
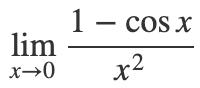
和上面那题一样,我们先使用和差化积对极限的分子进行变换,可以得到:
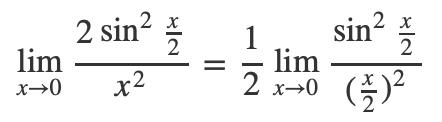
如果通过极限本身的定义来计算这个式子还是蛮复杂的,很难直观地获得答案。这个时候就需要用上换元法了,那么这个极限就可以转化成复合函数极限了。我们令 u = x/2,f(u) = sinu/u。因为当x趋向于0的时候,u也趋向于0,当u趋向于0的时候,f(u) 趋向于1,所以最终的极限就是1。
通过夹逼法和换元法,我们可以很方便地求解一些看起来比较棘手的极限。这也是我们求极限的过程当中使用非常频繁的方法。虽然上文当中的公式看起来有些比较麻烦,但是方法本身并不难,只要沉下心来,一定可以看明白的。
原创不易,希望我的文章可以给你带来收获。喜欢的话,请顺手点个关注或者转发吧,你们的支持是我最大的动力。
参考资料
同济大学《高等数学》第六版
程序员的数学