【剑指 Offer 65. 不用加减乘除做加法】
题目描述:
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/bu-yong-jia-jian-cheng-chu-zuo-jia-fa-lcof/
- 写一个函数,求两个整数之和,要求在函数体内不得使用 “+”、“-”、“*”、“/” 四则运算符号。
示例:
- 示例1:
输入: a = 1, b = 1
输出: 2
- 提示:
a, b 均可能是负数或 0
结果不会溢出 32 位整数
解析思路1:
- 十进制是人类使用的运算单位;而计算机只能识别二进制,计算机之所以能计算十进行运算,是因为在底层最终都是转化成二进制的运算,也就是 CPU的加法器。
- 参考点赞么?我知道你想看点不一样的题解解析(fengziL).有c++详细解题思想。
- 参考k神解析.有Python详细解题思想。
- 平时我们进行数学计算的使用的 “ + - * / ” 这些数学运算符,运算单位只有一种: 十进制。
- 而本题要求,不使用 运算符 “+”、“-”、“*”、“/” ,其实就是 不让 我们使用 十进制 来做计算。
- 这很容易就想到使用计算机本身的 二进制 代替 十进制 做计算。
需要注意的是,不使用 “+”、“-”、“”、“/”,是不使用十进制,而 “+”、“-”、“”、“/” 法,背后的 加法思想 减法思想 还是可以使用的。
参考十进制的加法公式:
从低位开始按位相加,逢10进一,累加到高位,依次进行得到最后结果。把 每一位 加法的输出分为:本位 和 进位

二进制的 位运算 操作符:
| 符号 | 称谓 | 运算规则 |
|---|---|---|
| ^ | 异或 | 两位不相同,结果为1 |
| & | 与 | 两位都为1,那么结果为1 |
那么对应 二进制加法 :每一位输出的情况是:

通过 异或 与 操作就完成了加法计算的 一半 (也叫半加器);
因为 异或 与 只计算了一半,它只能计算 一位 ,要计算第二位,就要考虑来自低位的进位,这样就是一个完整的 加法计算 (也叫全加器)。有了全加器,我们就能构造更复杂的加法器。
一个全加器可以计算一个位的加法,多个全加器组合,把低位的进位输出,作为高位的进位输入。
- 算法流程示意:
1、while循环模拟多个加法器;
2、本位/进位 的处理;
01 是计算后的本位,直接记录。11 是计算后的进位,需要:做 进位逻辑 后进入下轮计算。
(进位逻辑:乘以进制数,也就是 11 * 10),而这里没有下轮计算了,最终得到 111 。
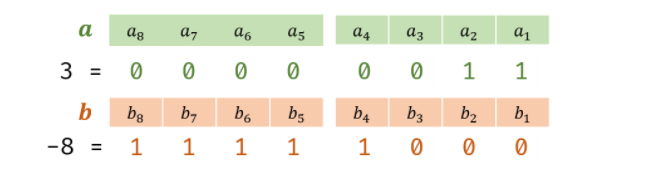
- 在二进制中:
如:3+(-8)- 计算进位 c: int c = a & b;
- 计算本位: a = a ^ b;
- 移位 ,退出循环,输出结果。
代码(cpp)
while 循环模拟多个加法器:
class Solution {
public:
int add(int a, int b) {
while (b) {
int c = a & b; // 计算 进位
a = a ^ b; // 计算 本位
b = (unsigned)c << 1; //(进位)<< 左移运算符是用来将一个数的各二进制位全部左移若干位,右补0 ;进位不存在负的情况,unsigned 是修饰限定 进位
}
return a;
}
};
递归 版本代码:
class Solution {
public:
int add(int a, int b) {
return b ? add(a ^ b, (unsigned)(a & b) << 1) : a;
}
};
复杂度分析:
- 时间复杂度 O(1);
- 空间复杂度 O(1) : 使用常数大小的额外空间。
代码(python)
Python,Java 等语言中的数字都是以 补码 形式存储的。但 Python 没有 int , long 等不同长度变量,即在编程时位数的概念。
- 参考k神-jyd解析.有Python详细解题思想。
class Solution:
def add(self, a: int, b: int) -> int:
x = 0xffffffff
a, b = a & x, b & x
while b != 0:
a, b = (a ^ b), (a & b) << 1 & x
return a if a <= 0x7fffffff else ~(a ^ x)
版权声明:本文为Kefenggewu_原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。