引用的文章:http://blog.csdn.net/xjz18298268521/article/details/51220576
https://blog.csdn.net/qq_37577735/article/details/80041586
双线性插值,又称为双线性内插。在数学上,双线性插值是有两个变量的插值函数的线性插值扩展,其核心思想是在两个方向分别进行一次线性插值。
示例:已知的红色数据点与待插值得到的绿色点
假如我们想得到未知函数f在点P= (x,y) 的值,假设我们已知函数f在Q11 = (x1,y1)、Q12 = (x1,y2),Q21 = (x2,y1) 以及Q22 = (x2,y2) 四个点的值。

首先在x方向进行线性插值,得到R1和R2,

然后在y方向进行线性插值,得到P.
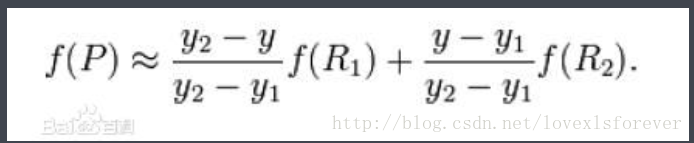
这样就得到所要的结果f(x,y).

其中红色点Q11,Q12,Q21,Q22为已知的4个像素点.
第一步:X方向的线性插值,在Q12,Q22中插入蓝色点R2,Q11,Q21中插入蓝色点R1;
第二步 :Y方向的线性插值 ,通过第一步计算出的R1与R2在y方向上插值计算出P点。
线性插值的结果与插值的顺序无关。首先进行y方向的插值,然后进行x方向的插值,所得到的结果是一样的。双线性插值的结果与先进行哪个方向的插值无关。
由于图像双线性插值只会用相邻的4个点,因此上述公式的分母都是1。
如果选择一个坐标系统使得 的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1),那么插值公式就可以化简为
f(x,y)=f(0,0)(1-x)(1-y)+f(1,0)x(1-y)+f(0,1)(1-x)y+f(1,1)xy。
写成矩阵形式就是
1-x x
1-y f(0,0) f(1,0)
y f(0,1) f(1,1)
例如,I(1.2,4.5)就是非整数的像素值,它的二维线性插值就是
1-xx xx
1-yy I(1,4) I(1,5)
yy I(2,4) I(2,5)
其中,xx为小数部分,此例中,xx=0.2, I(x,y)表示(y,x)处的像素值。