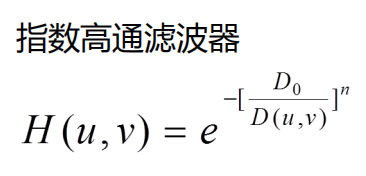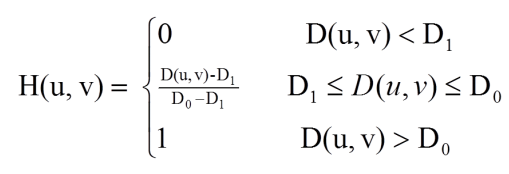一、实验目的与要求
1.了解频域变换过程,掌握频域变换特点
2.熟练掌握频域滤波中常用的平滑和锐化滤波器,能够对不同要求的图像进行滤波处理,体会并正确评价滤波效果,了解不同滤波方式的使用场合,能够从理论上作出合理的解释。
二、实验相关知识
图像增强是指按特定的需要突出一幅图像中的某些有用信息,同时消弱或去除某些不需要的信息的处理方法,其主要目的是使处理后的图像对某些特定的应用比原来的图像更加有效。图像平滑与锐化处理是图像增强的主要研究内容。
和本实验有关的几个常用Matlab函数:
(1) imnoise:用于对图像生成模拟噪声,如:
j=imnoise(i,‘gaussian’,0,0.02) %在图像i上叠加均值为0、方差为0.02的高斯噪声,得到含噪图像j
j=imnoise(i,‘salt & pepper’,0.04) %在图像i上叠加密度为0.04的椒盐噪声,得到含噪图像j
(2) fspecial:用于产生预定义滤波器,如:
h=fspecial(‘average’,3); %产生3×3模板的均值滤波器
h=fspecial(‘sobel’); %产生sobel水平边缘增强的滤波器
可选项还有:'gaussian’高斯低通滤波器、'laplacian’拉普拉斯滤波器、'log’高斯拉普拉斯滤波器等
(3) imfilter、filter2、conv2:均是基于卷积的图像滤波函数,都可用于图像滤波,用法类似,如:
i=imread(‘p1.tif’);
h=fspecial(‘prewitt’); %产生prewitt算子的水平方向模板
j1=imfilter(i,h); %或者j2=filter2(h,i); 或者j3=conv2(i,h);
(4) fft2:二维快速傅里叶变换函数
(5) fftshift:中心变换函数
(6) abs:取绝对值或复数取幅值
三、实验内容
1、图像频域平滑(去噪):使用自生成图像(包含白色区域,黑色区域,并且部分区域添加椒盐噪声),然后进行傅里叶变换,并且分别使用理想低通滤波器、巴特沃斯低通滤波器、指数低通滤波器和梯形低通滤波器(至少使用两种低通滤波器),显示滤波前后的频域能量分布图,空间图像。分析不同滤波器对噪声、边缘的处理效果及其优缺点。
(1)源代码
%自生成一个图像
I=zeros(300,300);
for i=1:300
for j=1:300
I(i,j)=0;%黑
end
end
K=imnoise(I,'salt & pepper',0.04) %加椒盐噪声
for i=100:200
for j=100:200
K(i,j)=1;%白
end
end
subplot(2,3,1);
imshow(K);
title('自生成图像');
s=fftshift(fft2(K));%先傅里叶变换,然后将傅里叶变化零频率搬移到频谱中间
subplot(2,3,2);
imshow(abs(s),[]);%abs取复数的幅值,[]自动调整数据的范围以便于显示
title('图像傅里叶变换所得频谱');
[a,b]=size(s);
a0=round(a/2);%确定傅里叶变化原点,并且数据取整
b0=round(b/2);
d0=15;%截止频率
d1=30;
n=2;
s1=zeros(a,b);%理想低通滤波
s2=zeros(a,b);%巴特沃斯低通滤波
s3=zeros(a,b);%指数低通滤波
s4=zeros(a,b);%梯形低通滤波
for i=1:a
for j=1:b
d=sqrt((i-a0)^2+(j-b0)^2);
if d<=d0
h1=1;
else
h1=0;
end
h2=1/(1+0.414*((d/d0)^(2*n)));
h3=exp(-0.347*(d/d0)^n);
if d<=d0
h4=1;
elseif d<=d1
h4=(d-d1)/(d0-d1);
else
h4=0;
end
s1(i,j)=h1*s(i,j);
s2(i,j)=h2*s(i,j);
s3(i,j)=h3*s(i,j);
s4(i,j)=h4*s(i,j);
end
end
s1=real(ifft2(ifftshift(s1)));%傅里叶逆移频,由于之前做过fftshift,然后傅里叶反变换,然后提取实部
subplot(2,3,3);
imshow(s1);
title('理想低通滤波所得图像');
s2=real(ifft2(ifftshift(s2)));
subplot(2,3,4);
imshow(s2);
title('巴特沃斯低通滤波所得图像');
s3=real(ifft2(ifftshift(s3)));
subplot(2,3,5);
imshow(s3);
title('指数低通滤波所得图像');
s4=real(ifft2(ifftshift(s4)));
subplot(2,3,6);
imshow(s4);
title('梯形低通滤波所得图像');
(2)实验结果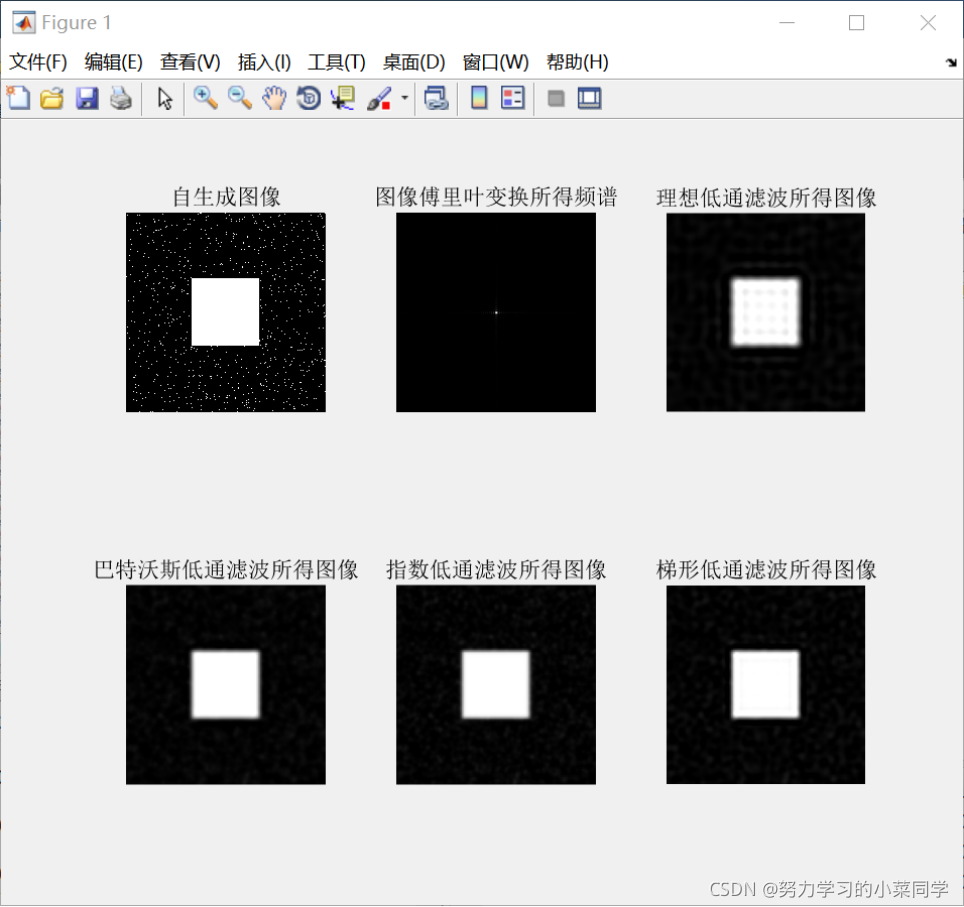
(3)实验分析
理想低通滤波器:由于高频成分包含有大量的边缘信息,因此采用该滤波器在去噪声的同时将会导致边缘信息损失而使图像边缘模糊。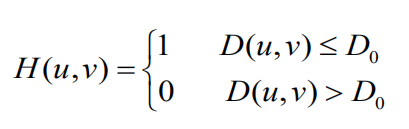
巴特沃斯低通滤波器:它的特性是连续性衰减,而不像理想滤波器那样陡峭变化,即明显的不连续性。因此采用该滤波器滤波在抑制噪声的同时,图像边缘的模糊程度大大减小,没有振铃效应。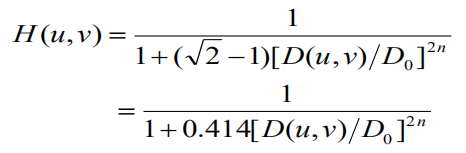
指数低通滤波器:采用该滤波器在抑制噪声的同时,图像边缘的模糊程度较用巴特沃斯滤波产生的大些,无明显的振铃效应。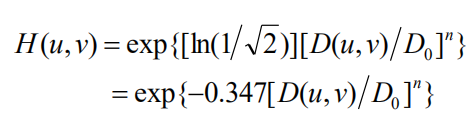
梯形低通滤波:采用该滤波器在抑制噪声的同时,图像边缘的模糊程度较用巴特沃斯滤波产生的大些,无明显的振铃效应。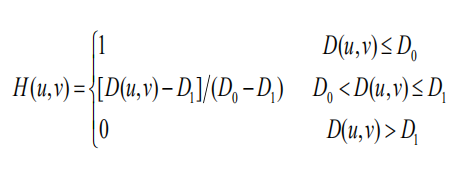
2、图像频域平滑(锐化):选择一幅图像,例如rice.png,分别使用理想高通滤波器、巴特沃斯高通滤波器、指数高通滤波器和梯形高通滤波器(至少使用两种高通滤波器),显示滤波前后的频域能量分布图,空间图像。分析不同滤波器处理效果及其优缺点。
(1)源代码
I=imread('C:\Users\Administrator\Pictures\test.png');
I=rgb2gray(I);
subplot(3,4,1);
imshow(I);
title('原图像');
s=fftshift(fft2(I));%先傅里叶变换,然后将傅里叶变化零频率搬移到频谱中间
subplot(3,4,2);
imshow(log(abs(s)),[]);
title('原图频谱');
[a,b]=size(s);
a0=round(a/2);%确定傅里叶变化原点,并且数据取整
b0=round(b/2);
d0=15;%截止频率
d1=30;
n=2;
s1=zeros(a,b);%理想高通滤波
s2=zeros(a,b);%巴特沃斯高通滤波
s3=zeros(a,b);%指数高通滤波
s4=zeros(a,b);%梯形高通滤波
for i=1:a
for j=1:b
d=sqrt((i-a0)^2+(j-b0)^2);
if d<=d0
h1=0;
else
h1=1;
end
h2=1/(1+(d0/d)^(2*n));
h3=exp(-(d0/d)^n);
if d<=d0
h4=0;
elseif d<=d1
h4=(d-d1)/(d0-d1);
else
h4=1;
end
s1(i,j)=h1*s(i,j);
s2(i,j)=h2*s(i,j);
s3(i,j)=h3*s(i,j);
s4(i,j)=h4*s(i,j);
end
end
s1=uint8(real(ifft2(ifftshift(s1))));%傅里叶逆移频,由于之前做过fftshift,然后傅里叶反变换,然后提取实部
subplot(3,4,3);
imshow(s1);
title('理想高通滤波所得图像');
s1new=fftshift(fft2(s1));
subplot(3,4,4);
imshow(log(abs(s1new)),[]);
title('理想高通滤波新频谱');
s2=uint8(real(ifft2(ifftshift(s2))));
subplot(3,4,5);
imshow(s2);
title('巴特沃斯高通滤波所得图像');
s2new=fftshift(fft2(s2));
subplot(3,4,6);
imshow(log(abs(s2new)),[]);
title('巴特沃斯高通滤波新频谱');
s3=uint8(real(ifft2(ifftshift(s3))));
subplot(3,4,7);
imshow(s3);
title('指数高通滤波所得图像');
s3new=fftshift(fft2(s3));
subplot(3,4,8);
imshow(log(abs(s3new)),[]);
title('指数高通滤波新频谱');
s4=uint8(real(ifft2(ifftshift(s4))));
subplot(3,4,9);
imshow(s4);
title('梯形高通滤波所得图像');
s4new=fftshift(fft2(s4));
subplot(3,4,10);
imshow(log(abs(s4new)),[]);
title('梯形高通滤波新频谱');
(2)实验结果

(3)实验分析
四种滤波函数的选用类似于低通。理想高通有明显振铃现象,即图像的边缘有抖动现象;巴特沃斯高通滤波效果较好,但计算复杂,其优点是有少量低频通过,H(u,v)是渐变的,振铃现象不明显;指数高通效果比巴特沃斯差些,振铃现象不明显;梯形高通会产生微振铃效果,但计算简单,较常用。
各个滤波函数如下: