题目:

分析:
日狗:原来有分配律: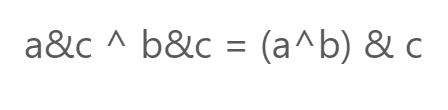
我当时的做法:
对于arr1 中的某个元素 a
对于arr2中的某个元素 [b1.b2…b3]
我们先只考虑 某一个a
(a and b1) xor (a and b2) xor (a and b3)
结果的二进制表示,某一位为0还是为1,由(a and b1),(a and b2) ,(a and b3)对应位置是0还是1决定。
那么当a的某一个位置是0,and的结果一定是0,0异或之后还是0.
那么当a的某一个位置是1,and的结果就是b1,b2,b3对应位置的数,异或的结果就取决于b1,b2,b3这些对应位置1的数目,1的个数是奇数,则异或结果为1,否则为0.
因此,先统计arr2中每个元素1的个数,然后对于arr1中的每个元素执行上述分析。
代码:
class Solution:
def getXORSum(self, arr1: List[int], arr2: List[int]) -> int:
max_ =0
for i in arr1:
max_=max(max_,i)
for i in arr2:
max_=max(max_,i)
n = len(bin(max_)[2:])*[0]
# 统计arr2中每个位置上的1的个数:
for i in arr2:
s = bin(i)[2:]
for j in range(0,len(s)):
if s[j]=='1':
n[j+len(n)-len(s)]+=1
ans=0
for i in arr1:
s = bin(i)[2:]
ss=''
for j in range(0,len(s)):
if s[j]=='0':
ss+='0'
elif n[j+len(n)-len(s)]%2==1:
ss+='1'
else:
ss+='0'
c=int(''.join(ss),2)
ans=ans^c
return ans
版权声明:本文为weixin_42721412原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。