人们认识用字母表示数的过程是很漫长的。对于"用字母表示数",初等代数史上有两个经典时刻:
第一个经典时刻 是公元 3 世纪,古希腊的丢番图在其著作《算术》中首次用字母表示数,他用音节第一个字母的缩写来表示未知量。未知量不同,音节不同,表示未知量的缩写字母不同,列出的方程也就不同,解方程的方法当然也不同。因而,丢番图解一个方程用一种方法,全凭高度的技巧。有人说:研究了丢番图一百个方程的解法后,还是不知道怎样去解第一百零一个方程。
第二个经典时刻 是 16 世纪,法国数学家韦达实现了历史性的突破,他不仅用固定的几个字母表示未知数,而且用某几个字母表示已知数,因而方程有了更一般的形式,解法也就有了更通用的办法,开创了符号代数的时代。因此,他被尊称为现代代数学之父。

每一个新的知识领域,不仅仅意味着新的概念和规则,更重要的是意味着新的思维方式。在代数知识的形成过程中,虽然也进行着抽象,但那已经带有更多的代数色彩。所以,要把握算术到代数的障碍,首要的是先分辨算术思维和代数思维的不同。 学生在代数知识的学习中,由于受算术思维的负迁移,必然会出现种种典型性的错误,如果教师视而不见听而不闻,也就失去了抽象深入推进的最好机会。
先来给你玩个魔法游戏吧:
第一步:你在1-10中选择一个数字(你也可以选择一个大于10的数字)
第二步:把这个数字加倍。
第三步:加上10。
第四步:除以2。
第五步:减去你一开始选择的那个数字。
你让孩子自己心算一下,然后让孩子不要说出来,你假装想一想,说:我猜你得到的数字一定是5,对吗?
孩子肯定会觉得很惊奇,为什么老师(爸爸)能猜到我心中想的数字呢?其实,这不过是一种"代数的把戏"!引入字母表示数其实才很简单,如果我们用n来表示任意一个数,于是就有了:
第一步:n;第二步:2n;第三步:2n+10;第四步:n+5;第五步:n+5-n;答案:5

可以说用字母替代数是数学发展史上的一件大事,是由算术跨越到代数的桥梁,是人类发展史上的一个飞跃,也是代数与算术的最显著的区别. "算术"可以理解为"计算的方法",而"代数"可以理解为"以符号替代数字",即"数学符号化".著名数学教育家波利亚曾说:"代数是一种不用词句而只用符号所构成的语言."
从算术到代数的跨越,是学生数学学习过程中极为重要的转变阶段,也是小学生向中学生的转变阶段.算术中的基本对象是数,包括数的表示、数的意义、数之间的关系、数的运算等,这些知识对学生是基本的,它们将为学生今后的代数学习打下坚实的基础.所不同的是,代数中的基本对象除了数,还出现了更具广泛意义的基本对象——符号,这是代数不同于算术的典型特征.在代数中,用字母替代数,用符号表示运算法则、运算性质、计算公式等,将数的知识提升到一般化的水平.在代数的课程中,学生要学习符号的意义、进行符号之间的运算(形式变换)和转换、用符号进行表示、用符号解决问题.在此过程中,学生还要学习许多新的概念,如代数式、方程、不等式、变量、参数、函数、图象等,而且他们还需要懂得代数的结构.因此,代数的内容和方法对学生提出了更高的要求,是学生所面对的又一次挑战.学生从算术到代数的跨越,是从对数的思考向对符号的思考的转变,是从算术思维向代数思维的转变,是思维层次从个别到一般、具体到抽象的飞跃.

用字母替代数使得数学更具有简洁的语言,能更普遍地说明数量关系,在列代数式、求代数式的值、形成公式等方面有广泛的应用.
1.(2019•霍邱县二模)2018年电影《我不是药神》反映了用药贵的事实,从而引起了社会的广泛关注.国家针对部分药品进行了改革,看病贵将成为历史.据调查,某种原价为345元的药品进行了两次降价,第一次降价15%,第二次降价的百分率为x,则该药品两次降价后的价格变为多少元?( )

【分析】根据题意可以用代数式表示出该药品两次降价后的价格,本题得以解决.
【解答】由题意可得,该药品两次降价后的价格变为:345(1﹣15%)(1﹣x),故选:A.
【点评】本题考查列代数式,解答本题的关键是明确题意,列出相应的代数式.
用到的知识点为:增长率=(新的价格–原价格)÷原价格×100%.


点评:本题主要考查的是有理数混合运算的拓展练习,找出其中的规律,引入字母,将复杂的问题简单化.


4.如图,有9个方格,要求每个方格填入不同的数,使得每行、每列、每条对角线上三个数的和相等,问图中的m是多少?
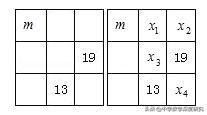
【分析】在该题中,未知量虽然比较多,虽然要求的只是右上角的数,但是题目的条件还与其他的数有关,因此,需恰当地引进不同的字母表示数,以便充分运用已知条件.

点评:本题涉及的量比较多,关系复杂,我们就巧妙地引入不同的字母,把数量关系表示出来,列出恰当的方程,最后求出要求的未知数的值.在解题中我们不需(或不能)求出所有字母的值,只需求出关键的字母的值,这种方法我们称之为"设而不求".
这里我强调的是教会孩子"学会思考",是孩子已经具备了数学思考的基本条件,也就是他们理解了数量概念,理解了运算符号的涵义,理解了算式表达的是什么,接下来,他们要学会用这些数学语言去解决问题,那么他们就需要学会,如何分析问题,进行思考。

我必须在深入谈这个问题前,再一次抛出我的观点:教会孩子如何思考并不是在浪费时间,也不会降低孩子的做题速度,这只是我们必要训练的第一目标,这个目标值得你花费60%的精力下去,剩下40%才是娴熟度的提高。著名的数学教育家波利亚就谈到过:"教会思考"意味着数学教师不仅仅应该传授知识,而且也应当去发展学生运用所传授的知识的能力;他应当强调运用的窍门,有益的心态及应有的思想习惯。