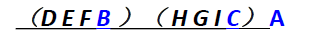数据结构基础：P3.3-树(一)---＞二叉树的遍历

本系列文章为浙江大学陈越、何钦铭数据结构学习笔记，前面的系列文章链接如下：
数据结构基础：P1-基本概念
数据结构基础：P2.1-线性结构—＞线性表
数据结构基础：P2.2-线性结构—＞堆栈
数据结构基础：P2.3-线性结构—＞队列
数据结构基础：P2.4-应用实例—＞多项式加法运算
数据结构基础：P2.5-应用实例—＞多项式乘法与加法运算-C实现
数据结构基础：P3.1-树(一)—＞树与树的表示
数据结构基础：P3.2-树(一)—＞二叉树及存储结构

文章目录

一、先序中序后序遍历

我们讲了二叉树的存储，接下来讲讲二叉树的遍历。我们后面主要是以二叉树的链式存储为主，来讲相应的遍历是怎么实现的。前面我们提到过二叉树的遍历最主要有4种形式：先序遍历 中序遍历 后序遍历 层次遍历。


1.1 先序遍历

遍历过程为：
①访问根结点；
②先序遍历其左子树；
③先序遍历其右子树。
这样的一种遍历过程实际上也是一种递归，我们要先序遍历这个树就变成是递归地遍历左子树跟递归地遍历右子树。

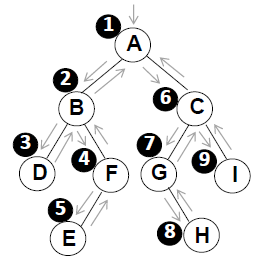
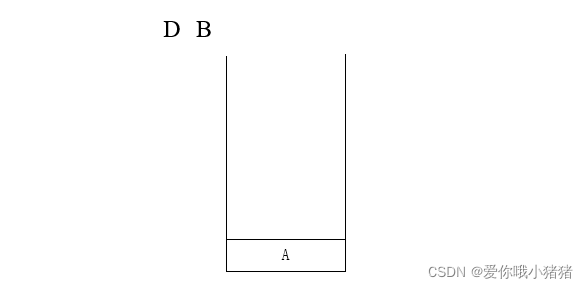
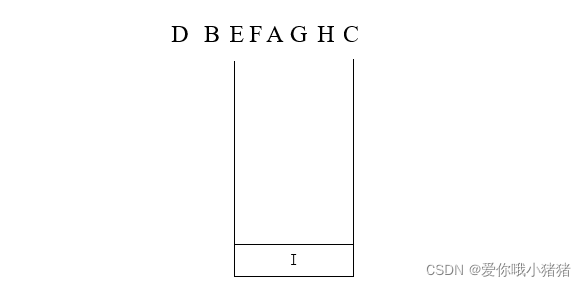
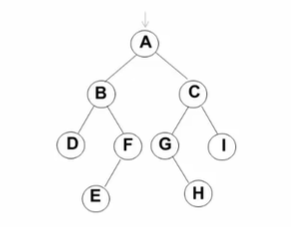
例：

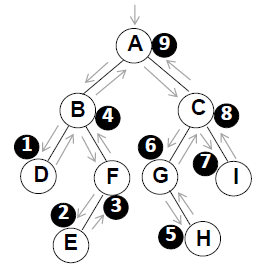
对于下边这样的一棵树，它的访问顺序如下：先序遍历=> A B D F E C G H I
在这里插入图片描述
它就满足了我们前面讲的这样的一个基本的过程：先是根，然后对左边递归，然后对右边递归。
①首先打印根结点A
②递归处理A的左子树，先打印A的左子树的根结点B
③递归处理B的左子树，先打印B的左子树的根结点D
④D没有子树，说明B的左子树已处理完毕。于是去递归处理B的右子树，先打印B的右子树的根结点F
⑤递归处理F的左子树，先打印F的左子树的根结点E
⑥E没有子树，说明F的左子树已处理完毕。于是去递归处理F的右子树。由于F没有右子树，说明F的子树已处理完毕，说明B的右子树已处理完毕。由于B的子树处理完了，说明A的左子树已处理完毕。于是去递归处理A的右子树，先打印A的右子树的根结点C
⑦递归处理C的左子树，先打印C的左子树的根结点G
⑧G只有右子树，于是去处理G的右子树H，打印H
⑨H没有子树，说明G的子树处理完毕，说明C的左子树处理完毕。于是去递归处理C的右子树，先打印C的右子树的根结点I
在这里插入图片描述

对应代码如下：

void PreOrderTraversal( BinTree BT )
{
	if( BT ) {
		printf("%d", BT->Data);
		PreOrderTraversal( BT->Left );
		PreOrderTraversal( BT->Right );
	}
}

1.2 中序遍历

遍历过程为：
①中序遍历其左子树；
②访问根结点；
③中序遍历其右子树。
如果你理解了刚才那个先序遍历过程，中序其实很简单，就是把访问根节点这个动作调到两次递归中间执行。

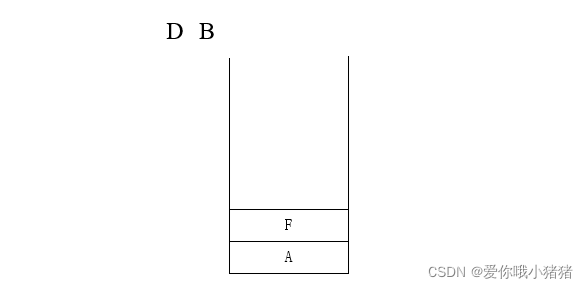
例：

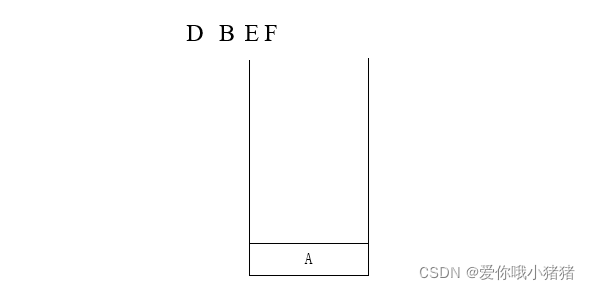
对于下边这样的一棵树，它的访问顺序如下：中序遍历=> D B E F A G H C I
在这里插入图片描述
也就是说整个的原则就是我们先左边 再根 再右边。然后又按照同样的规则继续递归。
①持续递归去找这棵树的左子树，直到找到最左侧的D，打印D
②D没有右子树，于是返回去打印D的父结点B
③持续递归去找B的右子树的最左侧的结点，找到E，打印E
④E没有右子树，于是返回去打印E的父结点F
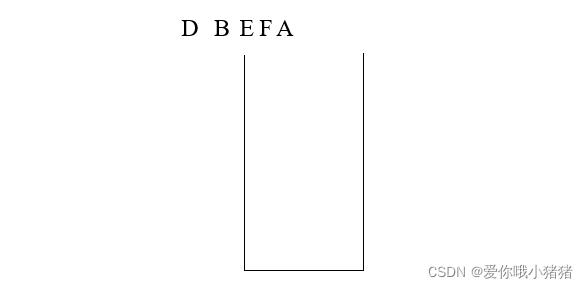
⑤F没有右子树，说明B的子树处理完了，向上返回，打印B的父结点A
⑥持续递归去找A的右子树的最左侧的结点，找到G，打印G
⑦G有右子树H，于是去递归处理H，由于H没有孩子，于是打印H
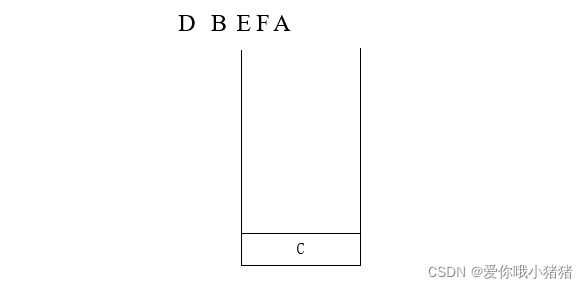
⑧G的子树处理完了，向上返回，打印G的父结点C
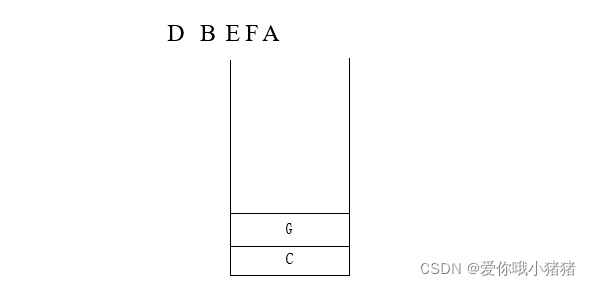
⑨递归处理C的右子树，打印I
在这里插入图片描述

对应的代码如下：

void InOrderTraversal( BinTree BT )
{
	if( BT ) {
		InOrderTraversal( BT->Left );
		printf("%d", BT->Data);
		InOrderTraversal( BT->Right );
	}
}

1.3 后序遍历

遍历过程为：
①中序遍历其左子树；
②中序遍历其右子树。
③访问根结点；
后序怎么做呢？很显然你把访问父结点的动作放到最后，也就是先左边再右边再根。

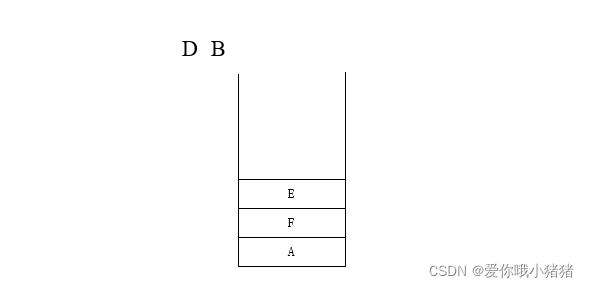
例：

对于下边这样的一棵树，它的访问顺序如下：后序遍历=> D E F B H G I C A
在这里插入图片描述
也就是说整个的原则就是：我们先左边 再右边 再根 。左边又按照同样的规则继续递归
①持续递归去找这棵树的左子树，直到找到最左侧的D。D没有子树，于是打印D
②D没有子树，说明B的左子树处理完毕，于是返回去递归处理B的右子树。找到B的右子树的最左侧的E，E没有子树，于是打印E
③E没有子树，说明F的左子树处理完毕，于是返回去递归处理F的右子树，F没有右子树，说明F子树处理完毕，打印F
④F的子树处理完毕，说明B的子树处理完毕，于是打印B
⑤B的子树处理完毕，说明A的左子树处理完了，于是去递归处理A的右子树。持续递归去找A的右子树的最左侧的结点，找到G。G有右子树H，于是去递归处理H。由于H没有子树，于是打印H
⑥H没有子树，说明G的子树处理完毕，于是打印G
⑦G的子树处理完毕，说明C的左子树处理完毕，于是递归处理C的右子树。C的右子树只有个I，且I没有子树，于是打印I
⑧C的子树处理完毕，于是打印C
⑨A的子树处理完毕，于是打印A
在这里插入图片描述

对应的代码如下：

void PostOrderTraversal( BinTree BT )
{
	if( BT ) {
		PostOrderTraversal( BT->Left );
		PostOrderTraversal( BT->Right);
		printf("%d", BT->Data);
	}
}

1.3 三种遍历代码实现效果对比

上面三个例子对应完整代码如下

#include <stdio.h>
#include <stdlib.h>

typedef char ElementType;
typedef struct TreeNode *BinTree;

struct TreeNode {
	ElementType Data;
	BinTree Left;
	BinTree Right;
};

void PreOrderTraversal(BinTree BT)
{
	if (BT) {
		printf("%c ", BT->Data);
		PreOrderTraversal(BT->Left);
		PreOrderTraversal(BT->Right);
	}
}

void InOrderTraversal(BinTree BT)
{
	if (BT) {
		InOrderTraversal(BT->Left);
		printf("%c ", BT->Data);
		InOrderTraversal(BT->Right);
	}
}

void PostOrderTraversal(BinTree BT)
{
	if (BT) {
		PostOrderTraversal(BT->Left);
		PostOrderTraversal(BT->Right);
		printf("%c ", BT->Data);
	}
}

int main(void)
{
	BinTree A = (BinTree)malloc(sizeof(struct TreeNode));
	BinTree B = (BinTree)malloc(sizeof(struct TreeNode));
	BinTree C = (BinTree)malloc(sizeof(struct TreeNode));
	BinTree D = (BinTree)malloc(sizeof(struct TreeNode));
	BinTree E = (BinTree)malloc(sizeof(struct TreeNode));
	BinTree F = (BinTree)malloc(sizeof(struct TreeNode));
	BinTree G = (BinTree)malloc(sizeof(struct TreeNode));
	BinTree H = (BinTree)malloc(sizeof(struct TreeNode));
	BinTree I = (BinTree)malloc(sizeof(struct TreeNode));

	A->Data = 'A', A->Left = B, A->Right = C;
	B->Data = 'B', B->Left = D, B->Right = F;
	C->Data = 'C', C->Left = G, C->Right = I;
	D->Data = 'D', D->Left = NULL, D->Right = NULL;
	E->Data = 'E', E->Left = NULL, E->Right = NULL;
	F->Data = 'F', F->Left = E, F->Right = NULL;
	G->Data = 'G', G->Left = NULL, G->Right = H;
	H->Data = 'H', H->Left = NULL, H->Right = NULL;
	I->Data = 'I', I->Left = NULL, I->Right = NULL;
	
	printf("先序遍历：\n");
	PreOrderTraversal(A);
	printf("\n");

	printf("中序遍历：\n");
	InOrderTraversal(A);
	printf("\n");

	printf("后序遍历：\n");
	PostOrderTraversal(A);
	printf("\n");

	return 0;
}

运行，效果如下，正确。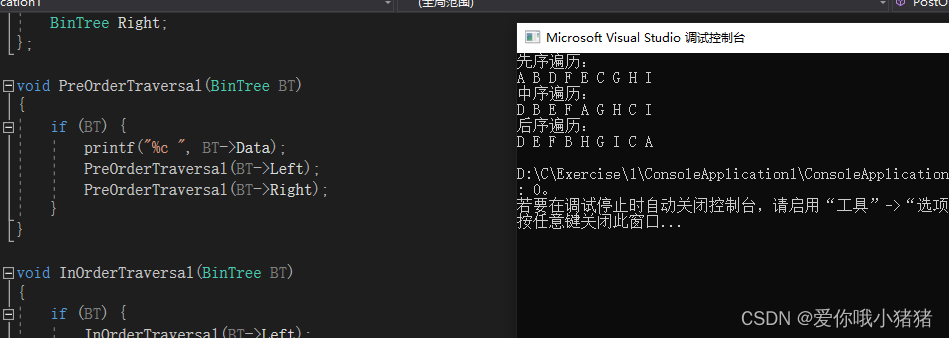
在这里插入图片描述


1.4 总结

总结

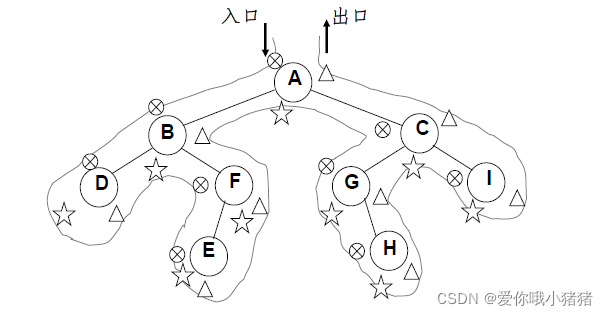
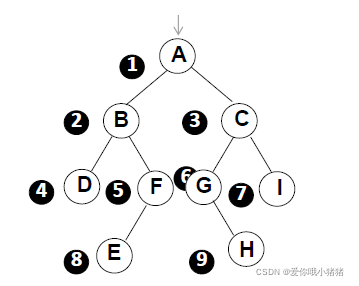
遍历过程中经过结点的路线一样，只是访问各结点的时机不同。下图中在从入口到出口的曲线上用❌、⭐、?三种符号分别标记出了先序、中序和后序访问各结点的时刻。
在这里插入图片描述
实际上：
每个结点我们有３次碰到它的机会。前序就是第一次碰到它的时候，就把它print出来。第二次碰到它的时候再printf出来那就叫中序。最后一次即第三次碰到它的时候再printf出来就叫后序。


二、中序非递归遍历

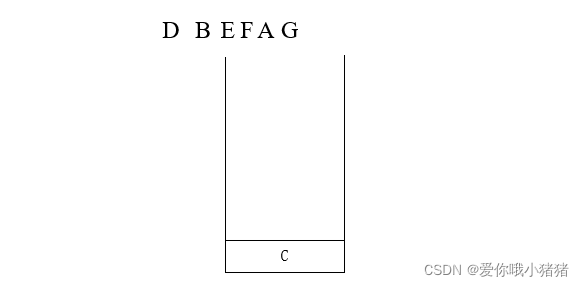
前面我们主要讲了三种遍历方法：先序 中序 后序。这三种遍历方法都是用递归来实现的，递归它根本的实现方法还是用堆栈。所以接下来我们想讲一件事情是：有没有可能我们直接用堆栈来实现，不用递归。所以这里我们就举一个例子 ，对中序遍历来讲，怎么样用堆栈来实现一个非递归的一个遍历算法。


2.1 算法流程

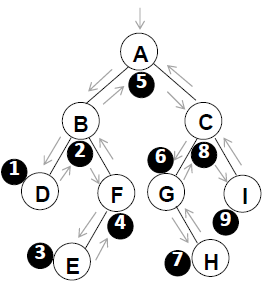
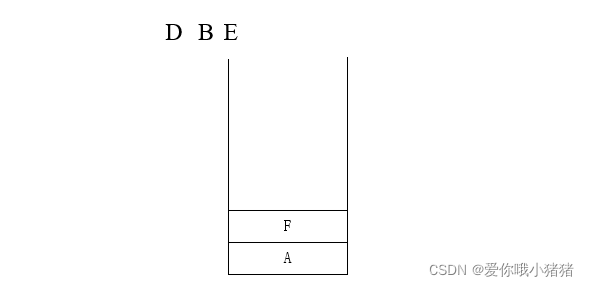
我们仍然使用前面那张图片，分析其中序遍历过程：
在这里插入图片描述
具体过程为：
1、碰到一个A，由于它是中序，必须把左边的子树都遍历完了之后才能够print。那左边子树遍历完了之后怎么知道又回到这边来呢，所以这个时候需要采用一个堆栈，把A放进去。
在这里插入图片描述
2、接下来往A的左边找，碰到B，放到堆栈里去。
在这里插入图片描述
3、接下来往B的左边找，碰到D，放到堆栈里去。
在这里插入图片描述
4、接下来往D的左边找，没了。这时候说明它就要往回走了，就从堆栈里面抛出来一个元素----D。
在这里插入图片描述
5、接下来往D的右边找，没了。这个时候再回去，从堆栈里再抛出一个元素----B。
在这里插入图片描述
6、接下来往B的右边找，碰到F，放到堆栈里去。
在这里插入图片描述
7、接下来往F的左边找，碰到E，放到堆栈里去。
在这里插入图片描述
8、接下来往E的左边找，没了。这个时候再回去，从堆栈里再抛出一个元素----E。
在这里插入图片描述
9、接下来往E的右边找，没了。这个时候再回去，从堆栈里再抛出一个元素----F。
在这里插入图片描述
10、接下来往F的右边走，没了。从堆栈里再抛出一个元素----A。
在这里插入图片描述
11、接着往A的右边走，碰到C，放到堆栈里面去。
在这里插入图片描述
12、接着往C的左边走，碰到G，放到堆栈里面去。
在这里插入图片描述
13、接着往G的左边走，没了。从堆栈里再抛出一个元素----G。
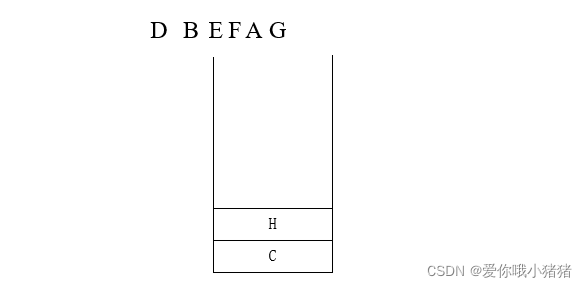
在这里插入图片描述
14、接着往G的右边走，碰到H，放到堆栈里面去。
在这里插入图片描述
15、接着往H的左边走，没了。从堆栈里再抛出一个元素----H。
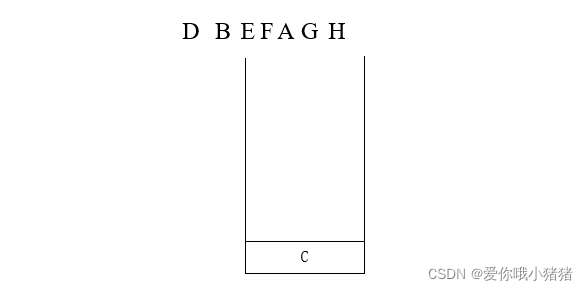
在这里插入图片描述
16、接着往H的右边走，没了。从堆栈里再抛出一个元素----C。
在这里插入图片描述
17、接着往C的右边走，碰到I，放到堆栈里面去。
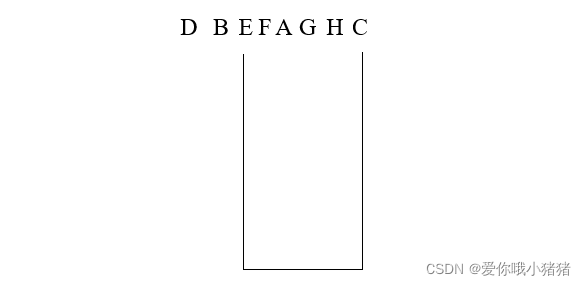
在这里插入图片描述
18、接着往I的左边走，没了。从堆栈里再抛出一个元素----I。
在这里插入图片描述
19、堆栈空了，结束。
整体流程动图如下：
在这里插入图片描述

流程总结如下：

中序遍历非递归遍历算法流程：
①遇到一个结点，就把它压栈，并去遍历它的左子树；
②当左子树遍历结束后，从栈顶弹出这个结点并访问它；
③然后按其右指针再去中序遍历该结点的右子树。
既然是这样的一个堆栈的操作，我们就直接用循环来实现了。它的基本思路是这样的：碰到一个结点就把它压到堆栈里去，然后遍历它的左子树。有左子树就往左边走，再有左子树就再往左边走，一直走到底。左边走到底的时候，这个时候从栈顶抛出一个元素然后把它print出来。接下来往右边走，访问它的右子树，然后再回到前面去。右子树的这个结点出发再往左边走，回到第一步。


2.2 代码

先序遍历、中序遍历的非递归遍历算法整体代码和测试效果如下

#include <stdio.h>
#include <stdlib.h>
#define MaxSize 10
typedef char ElementType;

//定义二叉树结点
typedef struct TreeNode *BinTree;
struct TreeNode {
	ElementType Data;
	BinTree Left;
	BinTree Right;
};

//定义堆栈，     堆栈里面有两个成员
//Bintree*指针： BinTree数组的地址，存放若干个BinTree
//Top：          栈顶元素的下标
typedef struct StackStruct *Stack;
struct StackStruct {
	BinTree *Data;
	int Top;
};

Stack CreatStack()
{ 
	Stack S;
	S = (Stack)malloc(sizeof(struct StackStruct));
	S->Data = (BinTree*)malloc(sizeof(BinTree)*MaxSize);
	S->Top = -1;
	return S;
}

int IsEmpty(Stack S)
{
	return S->Top == -1? 1 : 0;
}

void Push(Stack S, BinTree T)
{
	S->Data[++S->Top] = T;
}

BinTree Pop(Stack S)
{
	return S->Data[S->Top--];
}

void PreOrderTraversal(BinTree BT)
{
	BinTree T = BT;
	Stack S = CreatStack(); /*创建并初始化堆栈S*/
	while (T || !IsEmpty(S)) {
		while (T) { /*一直向左并将沿途结点压入堆栈*/
			printf("%c ", T->Data); /*（访问）打印结点*/
			Push(S, T);
			T = T->Left;
		}
		if (!IsEmpty(S)) {
			T = Pop(S); /*结点弹出堆栈*/
			T = T->Right; /*转向右子树*/
		}
	}
}

void InOrderTraversal(BinTree BT)
{
	BinTree T = BT;
	Stack S = CreatStack(); /*创建并初始化堆栈S*/
	while (T || !IsEmpty(S)) {
		while (T) { /*一直向左并将沿途结点压入堆栈*/
			Push(S, T);
			T = T->Left;
		}
		if (!IsEmpty(S)) {
			T = Pop(S); /*结点弹出堆栈*/
			printf("%c ", T->Data); /*（访问）打印结点*/
			T = T->Right; /*转向右子树*/
		}
	}
}


int main(void)
{
	BinTree A = (BinTree)malloc(sizeof(struct TreeNode));
	BinTree B = (BinTree)malloc(sizeof(struct TreeNode));
	BinTree C = (BinTree)malloc(sizeof(struct TreeNode));
	BinTree D = (BinTree)malloc(sizeof(struct TreeNode));
	BinTree E = (BinTree)malloc(sizeof(struct TreeNode));
	BinTree F = (BinTree)malloc(sizeof(struct TreeNode));
	BinTree G = (BinTree)malloc(sizeof(struct TreeNode));
	BinTree H = (BinTree)malloc(sizeof(struct TreeNode));
	BinTree I = (BinTree)malloc(sizeof(struct TreeNode));

	A->Data = 'A', A->Left = B, A->Right = C;
	B->Data = 'B', B->Left = D, B->Right = F;
	C->Data = 'C', C->Left = G, C->Right = I;
	D->Data = 'D', D->Left = NULL, D->Right = NULL;
	E->Data = 'E', E->Left = NULL, E->Right = NULL;
	F->Data = 'F', F->Left = E, F->Right = NULL;
	G->Data = 'G', G->Left = NULL, G->Right = H;
	H->Data = 'H', H->Left = NULL, H->Right = NULL;
	I->Data = 'I', I->Left = NULL, I->Right = NULL;
	
	printf("先序遍历：\n");
	PreOrderTraversal(A);
	printf("\n");

	printf("中序遍历：\n");
	InOrderTraversal(A);
	printf("\n");


	return 0;
}

运行，可以看出结果正确。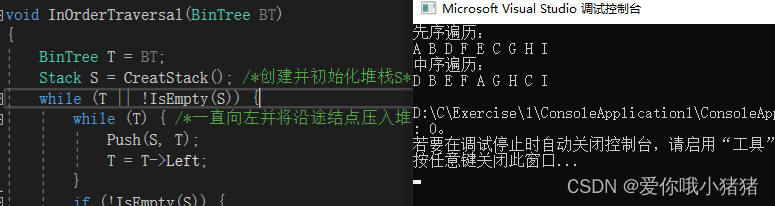
在这里插入图片描述
后序遍历要麻烦一些，这里不单独讲解。


三、层序遍历

3.1 二叉树遍历的本质与问题

前面我们介绍了前序 中序 后序这三种遍历的递归方式跟非递归方式，我们还有第4种遍历方法，就是层序遍历。在讲这个方法之前，我们再来想一想，二叉树遍历的核心问题是什么。

二叉树遍历的本质：
二叉树是二维结构，我们遍历就要产生一个序列。而这个序列是一维的，线性结构。所以二叉树的遍历其本质就是怎么样把一个二维结构变成一个一维的线性序列的过程。对于同样的一个二维结构，你使用不同的遍历方法，就产生不同的一维序列。那么二维怎么变成一维，我们的难点和问题在哪里？
二叉树遍历的问题:
访问到一个结点的时候，我们可以根据其指针域找到它的左右儿子，进而进行访问。当我们到了它的左儿子这个结点的时候，这个时候我们就有一个问题了：访问完左儿子后，我如何去找到右儿子？我如何向上找到自己本身这个结点？也就是说：一个结点跟它关联的是两个(左儿子与右儿子)，它访问了其中一个之后另外一个怎么办，或者它自己怎么办。它自己如果也忘掉了，右儿子也忘掉了，那么右儿子是永远访问不到了。
解决办法：
使用堆栈或者队列来保存这些结点。前面我们提到了前序 中序 后序遍历都用堆栈来保存自己这个结点。同样的，我们也可以用队列来保存未来要访问的结点。

总结：

二叉树遍历的核心问题：二维结构的线性化
①从结点访问其左、右儿子结点
②访问左儿子后，右儿子结点怎么办？
----需要一个存储结构保存暂时不访问的结点
----存储结构：堆栈、队列


3.2 层序遍历

使用堆栈与队列保存结点：

当我们用堆栈保存未来要访问的结点时：我访问完当前结点后，开始访问左儿子，这个时候把自己保存起来。将来回来的时候我再去访问右儿子。
当我们用队列保存未来要访问的结点时：我访问完当前结点后，开始访问左儿子，这个时候把右儿子保存起来。将来直接从队列里面找到右儿子进行访问。

使用队列保存结点：

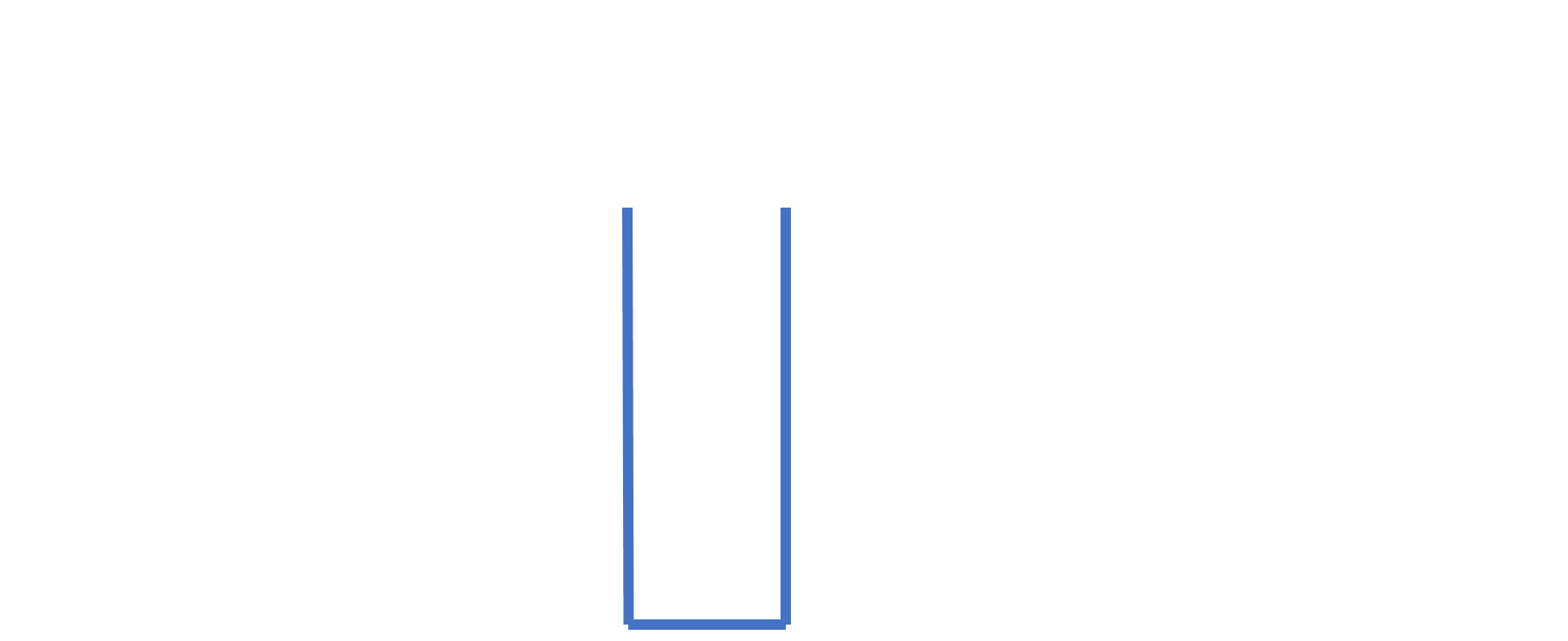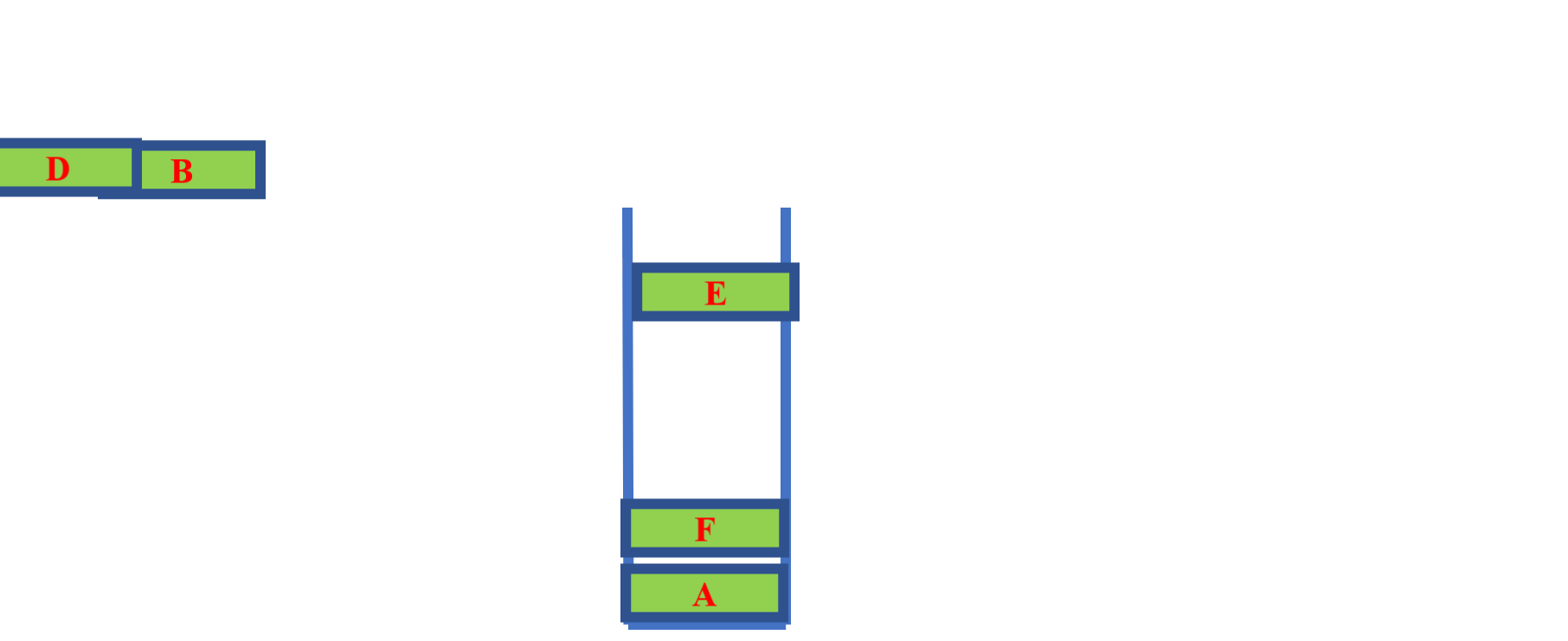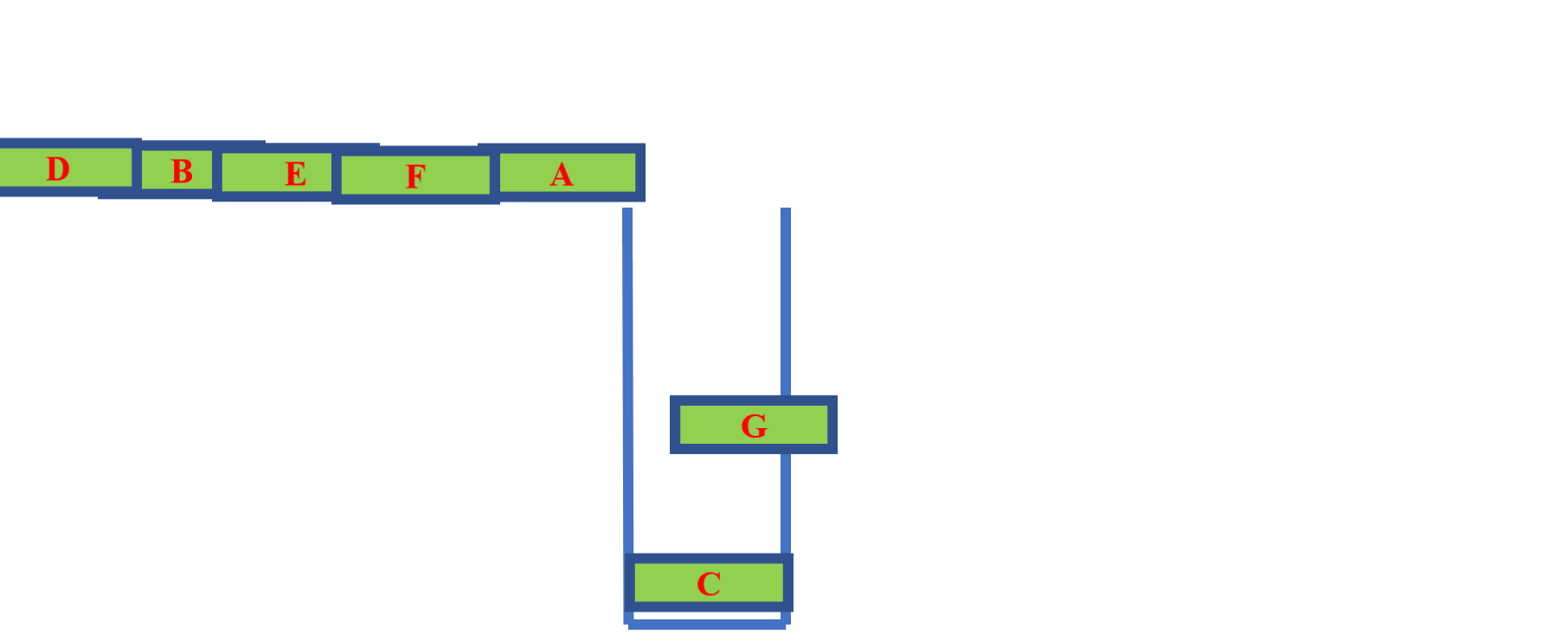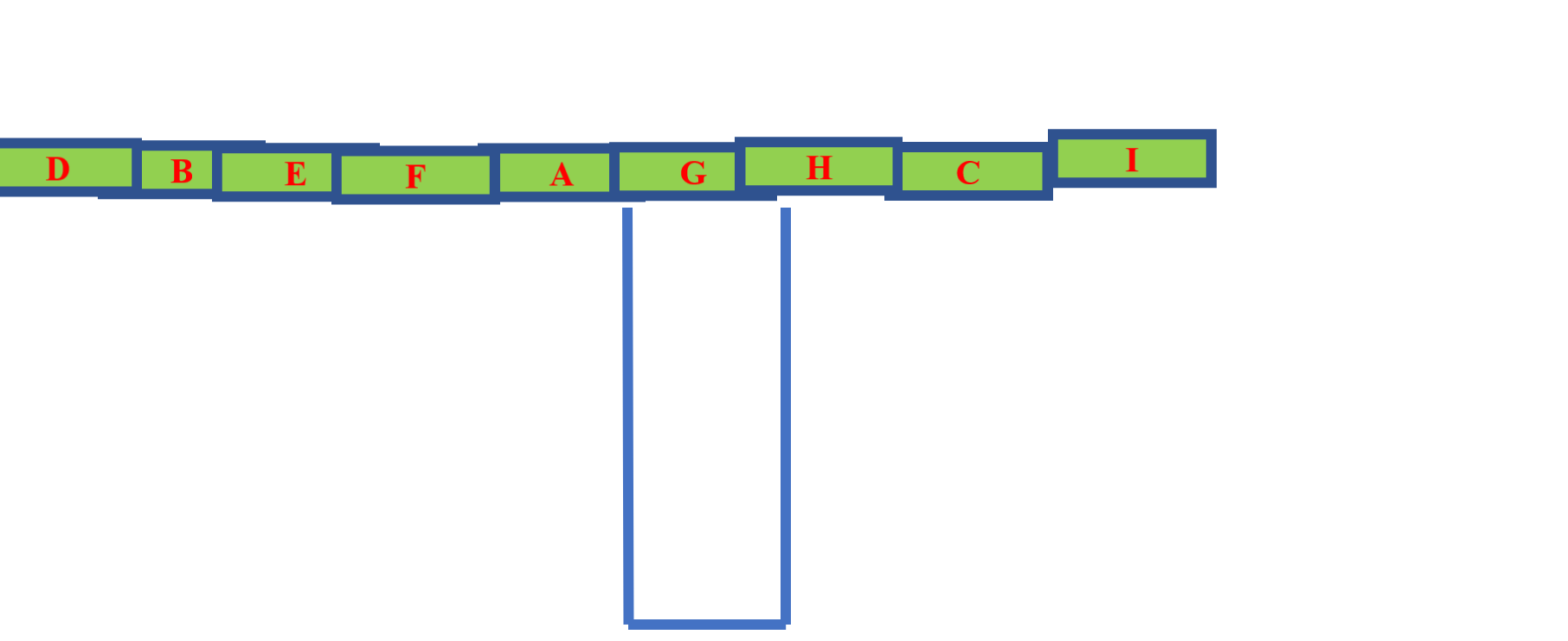
从根结点开始 ，首先根结点进入这个队列。进入队列之后，接下来做一个循环，每次循环就是基本的过程就这样的：从队列里面拎出一个元素访问该结点，然后把这个结点的左右儿子放到队列里面去，再进入下一个循环。再从队列里面拎出一个元素出来，访问这个结点，再把它的左右儿子放到队列里去…
总结：遍历从根结点开始，首先将根结点入队，然后开始执行循环：结点出队、访问该结点、其左右儿子入队

例子：

下面我们来看这样的一个例子，在这个例子里面我们用一个队列对这个整个过程进行访问。
在这里插入图片描述
访问过程如下：
①先从根结点开始，把这个A放到队列里去。
接下来开始做循环了，每次循环做2件事情：
----从队列里面抛出一个元素 print出来
----然后把左右儿子放进去
②将A抛出，并print。输出A。
③A的左右孩子B C入队列，然后再抛出一个元素并print。输出B
④B的左右孩子D F入队列，然后再抛出一个元素并print。输出C
⑤C的左右孩子G I入队列，然后再抛出一个元素并print。输出D
⑥D没有孩子，再抛出一个元素并print。输出F
⑦F的左孩子E入队列，然后再抛出一个元素并print。输出G
⑧G的右孩子H入队列，然后再抛出一个元素并print。输出I
⑨I没有孩子，再抛出一个元素并print。输出E
⑩E没有孩子，再抛出一个元素并print。输出H
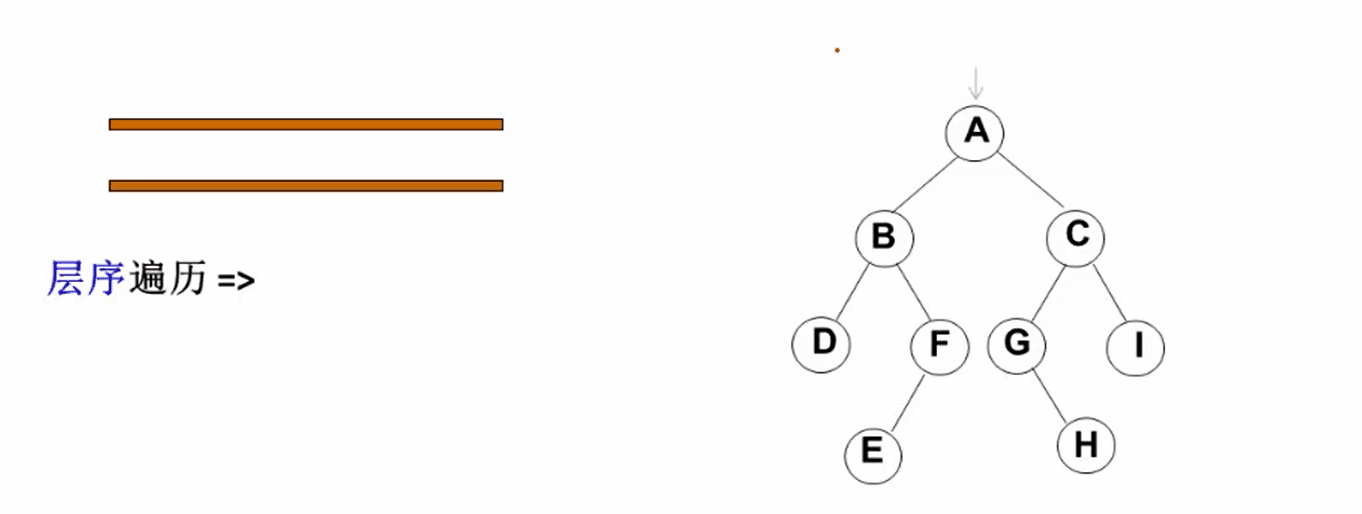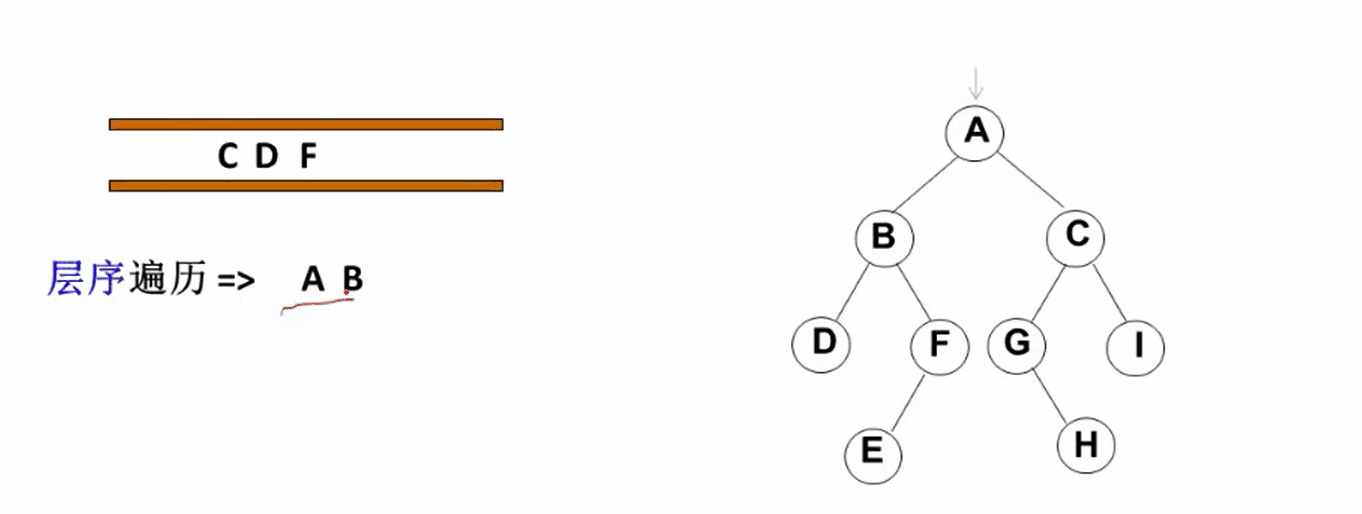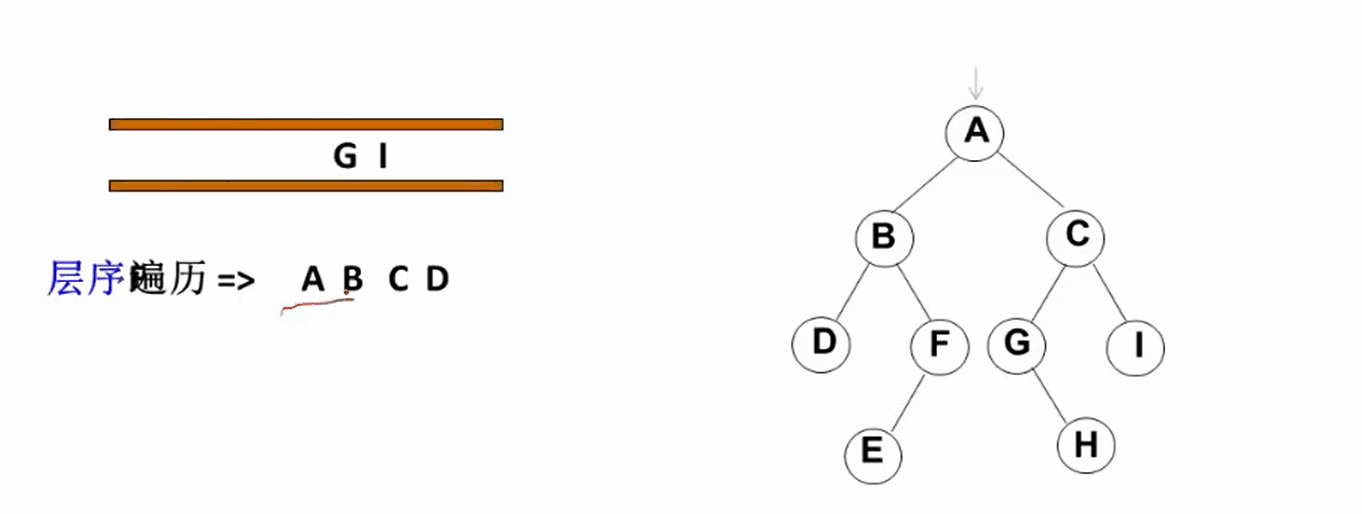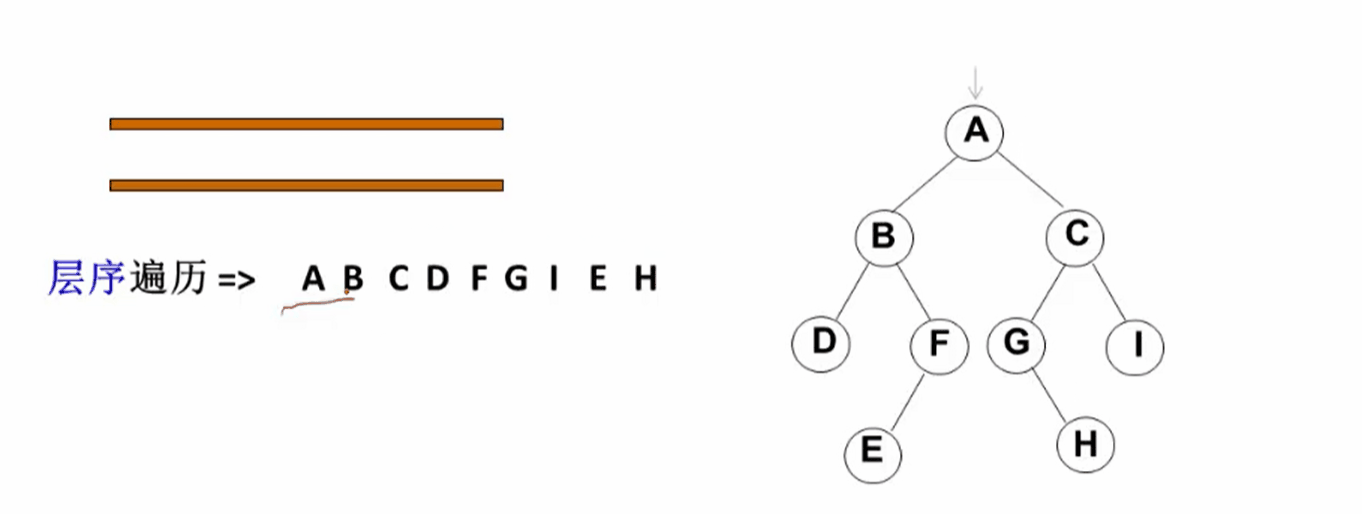
结束，结果为：ABCDFGIEH
访问过程动图如下：
在这里插入图片描述
最后各结点访问顺序如下：
在这里插入图片描述
这个序列有什么特征
这个序列特征是一层一层访问的，先是Ａ，接下来是ＢＣ，接下里是ＤEG I，接下来是EH。所以这就是说，我们用队列实现了按层序遍历的这样的一种方法，这是我们访问的顺序。

整个过程对应代码如下

void LevelOrderTraversal ( BinTree BT )
{ 
	Queue Q; BinTree T;
	if ( !BT ) return; /* 若是空树则直接返回 */
	Q = CreatQueue( MaxSize ); /*创建并初始化队列 根结点放到队列里面去Q*/
	AddQ( Q, BT );
	/*
	然后接下来是一个循环
	循环做三件事情:
	第一件事情 从队列里面抛出一个元素
	第二件事情 把队列刚抛出元素的Data print出来
	第三件事情 是把它的左右儿子放到队列里去
*/
	while ( !IsEmptyQ( Q ) ) {
		T = DeleteQ( Q );
		printf("%d\n", T->Data); /*访问取出队列的结点*/
		if ( T->Left ) AddQ( Q, T->Left );
		if ( T->Right ) AddQ( Q, T->Right );
	}
}

总结：

层序基本过程：先根结点入队，然后：
①从队列中取出一个元素；
②访问该元素所指结点；
③若该元素所指结点的左、右孩子结点非空， 则将其左、右孩子的指针顺序入队。


四、遍历应用例子

利用二叉树遍历这样的一种程序框架或者是思想，我们可以做许多有关二叉树方面的一些应用的一些问题。

4.1 输出二叉树中的叶子结点

首先我们来看一个例子：给你一个二叉树，要求你输出二叉树当中的叶子结点。也就是说，把二叉树里面所有没有儿子的结点全部输出。

思路：

要解决这个问题，可以在原来树遍历的基础上面把那个程序稍微改改就行了。比方说现在把前序遍历的程序改一改。前序遍历就三句话：print，然后两个递归。现在我们在print之前加个if判断，如果左右两边都没有儿子了，说明它是叶结点了，，这个时候就print出来，否则的话就不要print。

对应代码如下

void PreOrderPrintLeaves( BinTree BT )
{
	if( BT ) {
		if ( !BT-Left && !BT->Right )
			printf("%d", BT->Data );
		PreOrderPrintLeaves ( BT->Left );
		PreOrderPrintLeaves ( BT->Right );
	}
}

4.2 求二叉树的高度

一个二叉树的高度等于左右两个子树的最大高度加上1。求树高这个问题，我们要求一个树的高度，我们必须知道左右两个子树的高度。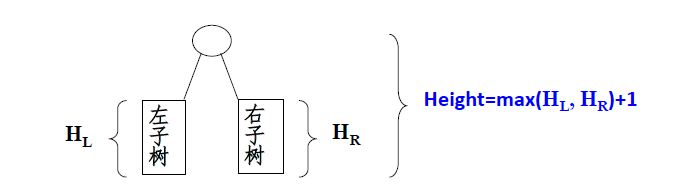
在这里插入图片描述
这个程序应该是通过改造那个后续遍历的那个程序。先左边递归，求出左子树的高度。再右边递归，求右子树的高度。最后将最大值加1。

int PostOrderGetHeight( BinTree BT )
{ 
	int HL, HR, MaxH;
	if( BT ) {
		HL = PostOrderGetHeight(BT->Left); /*求左子树的深度*/
		HR = PostOrderGetHeight(BT->Right); /*求右子树的深度*/
		MaxH = （HL > HR）? HL : HR; /*取左右子树较大的深度*/
		return ( MaxH + 1 ); /*返回树的深度*/
	}
	else return 0; /* 空树深度为0 */
}

4.3 二元运算表达式树及其遍历

表达式可以用树来表示。比方说我们给出这样的一棵表达式树，它里面的每个结点包含两类元素：如果是叶结点，它代表的是运算数，非叶结点是运算符号。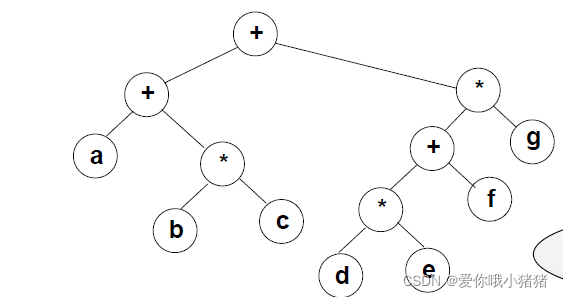
在这里插入图片描述


我们把这个表达式树遍历一下，看看是什么结果。

三种遍历可以得到三种不同的访问结果：
先序遍历得到前缀表达式：+ + a * b c * + * d e f g
中序遍历得到中缀表达式：a + b * c + d * e + f * g
后序遍历得到后缀表达式：a b c * + d e * f + g * +
然而中序遍历出来的结果是有问题的，它会受到运算优先级的影响。在这棵树中想表达的应该是a+b*c+(d*e+f)*g。
解决办法为：
每开始一次左子树操作，加个左括号。左子树操作结束后，加上右括号。因此，结果为：((a+(b)*c))*((((d)*e)+f)*g)。


4.4 由两种遍历序列确定二叉树

问题：已知三种遍历中的任意两种遍历序列，能否唯一确定一棵二叉树呢？
答案：必须要有中序遍历才行

没有中序的困扰：

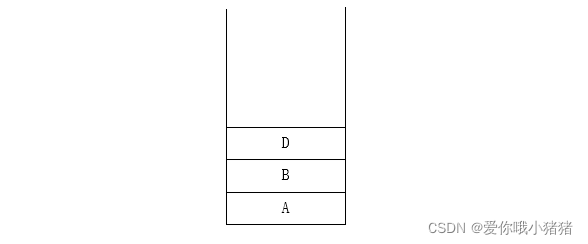
比方说告诉你前序遍历序列是A B ，后序遍历序列是B A，你给我确定一个二叉树。我们会发现，跟这两个序列一致的二叉树不止一棵，如下面两个。
先序遍历序列：A B
后序遍历序列：B A
在这里插入图片描述
我们可能不能唯一地确定一个二叉树，这是因为我们前序是根左右，后序是左右根。根是容易确定的，先序的第一个就是根，后序的最后一个就是根，但是左右的边界在哪里不知道，所以就导致了没法唯一地确定一棵二叉树。


4.5 先序和中序遍历序列来确定一棵二叉树

问题：如何通过先序和中序遍历序列来确定一棵二叉树
分析：

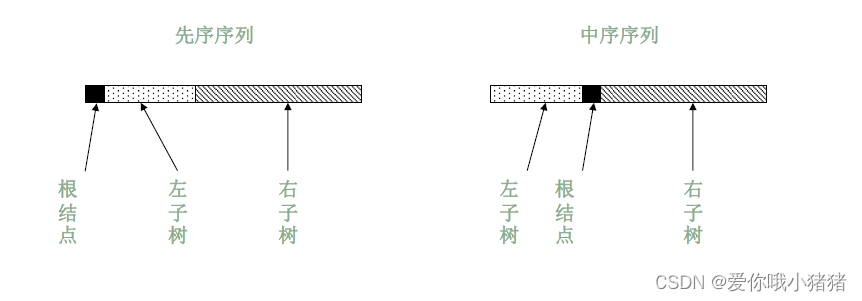
前序遍历是根 左 右，中序呢是左 根 右。
在这里插入图片描述
①前序序列里面第一个就是根，我知道了这个根就可以在中序序列里面去找到这个元素。在中序序列中找到这个元素了后，前面这一段就是左子树的中序序列，后面这一段是右子树的中序序列。
②在中序序列中去数左子树的个数，对应去先序序列的根结点后面往后数，找到左子树和右子树的先序序列。
③继续以左子树的根结点为起点，继续递归地执行前面两步，直到确定出左子树的结构。
④以右子树的根结点为起点，继续递归地执行最前面两步，直到确定出右子树的结构


下面举一个具体的例子
先序序列： a b c d e f g h i j
中序序列：c b e d a h g i j f

分析：

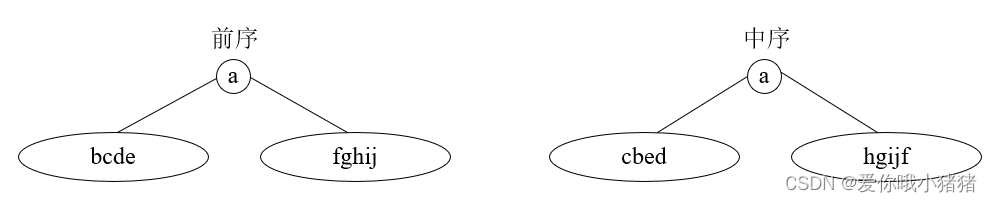
①先序里面第一个就是根，所以a就是整个树的根。
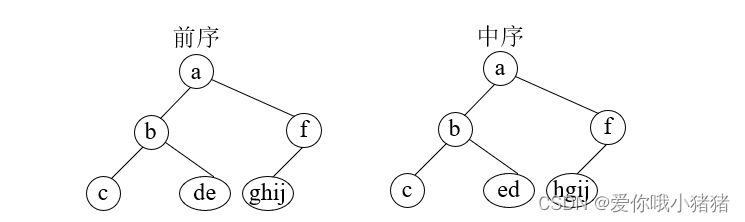
②我们知道根之后，到中序序列去找。找着这个a之后，将左右子树的先序和后序树结构画出来，如下：在这里插入图片描述
③重复上面的步骤，将起点分别设置为左右子树的根结点b和f。
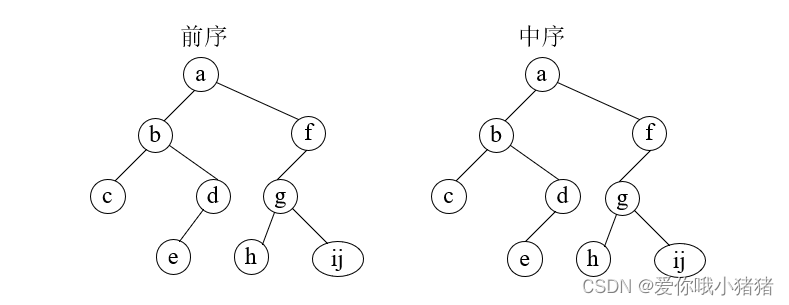
在这里插入图片描述
④重复上面的步骤
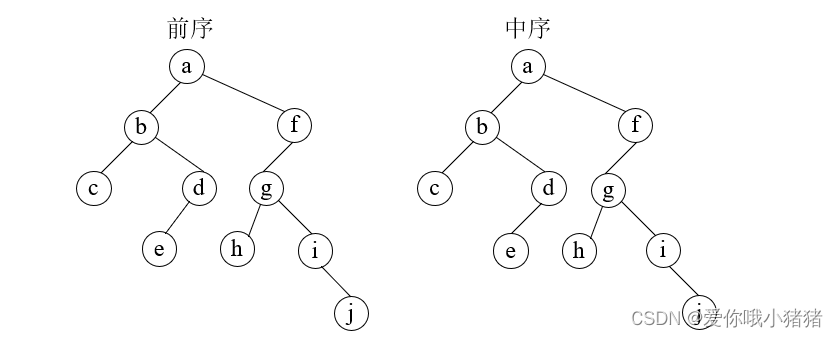
在这里插入图片描述
⑤再次重复上面的步骤，直到没有可以分解的结点。
在这里插入图片描述


五、小测验

1、假定只有四个结点A、B、C、D的二叉树，其前序遍历序列为ABCD，则下面哪个序列是不可能的中序遍历序列？

A. ABCD
B. ACDB
C. DCBA
D. DABC

答案：D

2、对于二叉树，如果其中序遍历结果与前序遍历结果一样，那么可以断定该二叉树________

A. 是完全二叉树
B. 所有结点都没有左儿子
C. 所有结点都没有右儿子
D. 这样的树不存在

答案：B

3、已知一二叉树的后序和中序遍历的结果分别是FDEBGCA 和FDBEACG，那么该二叉树的前序遍历结果是什么？

A. ABDFECG
B. ABDEFCG
C. ABDFEGC
D. ABCDEFG

答案：A

版权声明：本文为InnerPeaceHQ原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接和本声明。