JAVA ----斐波那契数列的思路及实现

定义：又称黄金分割数列，因数学家列昂纳多.斐波那契以兔子繁殖为例子而引入，故又称兔子数列，具体指的是这样一个数列：1,1,2,3,5,8,13,21，34..........F(1)=1,F(2)=1,F(n)=F( n-1)+F(n-2)  (n>=3),即后一个数等于前两个数字之和。

问题：斐波那契数列 求前10项。

实现：

思路一：递归

分析：

 F（1）=1         ，       F（2）=1

 F(3)=F(1)+F(2)=2

 F（4）=F（3）+F（2）=3

F（5）=F（4）+F（3）=5

.........

F(n)=F(n-1)+F(n-2)

程序代码：

import java.util.Scanner;
class test01{
    public static void main(String[]args){
        Scanner scanner=new Scanner(System.in);
        System.out.print("请输入一个数：");
            int m=scanner.nextInt();

       
        for(int n=1;n<=m;n++){
            System.out.println(fibo(n));
        }
    }
    
     public static int fibo (int n){
        if(n==1||n==2){                 //如果n为1或者为2则直接输出1
            return 1;
        }
        return fibo(n-1)+fibo(n-2);    //否则的话输出前一项和前前一项的和。
    }
}

输出结果：输入5

思路二：迭代

分析：

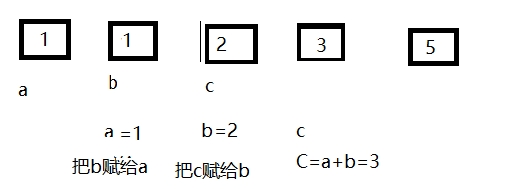
a=1,b=2  ,  c=a+b=2

计算第四项的时候，把b赋给a,所以第二项为a=1;把c赋给b,所以第三项为b=2；因此第四项为c=a+b=3.简单的说就是后一项等于前两项之和。

程序代码：

import java.util.Scanner;
class test01{
    public static void main(String[]args){
        Scanner scanner=new Scanner(System.in);
        System.out.print("请输入一个数：");
            int n=scanner.nextInt();
        fibolterator(n);
    }
     public static void fibolterator(int n){
        int a=1;
        int b=1;
        System.out.println(a);
        System.out.println(b);
        int count=2;              //从2开始算，如果count=输入的数就退出
        int c;
        while(true){
            c=a+b;
            System.out.println(c);
            count++;
            if(count==n){
                return;
            }
            a=b;
            b=c;
        }
    }
}

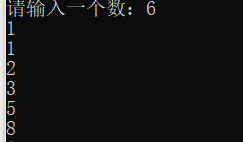
输出结果：输入6

最后我想说的是：迭代思路求斐波那契数列第n项时间复杂度为O(n)，空间复杂度为O(1)。相比递归方式，更推荐使用迭代求解斐波那契问题。相比递归其唯一的缺点可能就是可读性没有递归方式高。
 

斐波那契就讲到这啦。