目录
一、什么是p值
在假设检验中,证明备择假设H₁存在困难,我们就去证明它的反面原假设H0。P值实际上是当H0假设为真,一些极端情况出现的概率,如果P值很小,说明这种情况发生的概率很小。如果这种情况出现了,根据小概率原理,我们就有理由拒绝原假设,P值越小,拒绝原假设的理由越充分。
P值是H0能被拒绝的最小值。α是上限控制值
二、双侧检验的p值

若p值≥α/2,不拒绝H0
若p值<α/2,拒绝H0
三、单侧检验的p值

若p值≥α,不拒绝H0
若p值<α,拒绝H0
四、假设检验中双侧假设和单侧假设的决策范式α
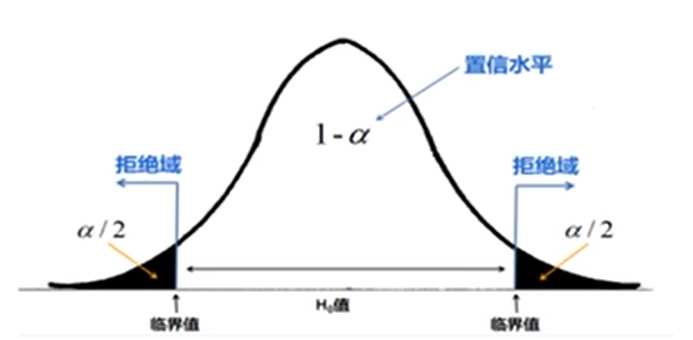
4.1 双侧检验
1.拒绝域在统计分布的两侧,有两个拒绝域,两个临界值,每个拒绝域的面积为α/2
2.只要μ>μ0或μ<μ0二者之中有一个成立,就可以拒绝原假设(μ0是原假设H0的总体均值,前句话的意思就是当μ落到拒绝域里时,就可以拒绝原假设)
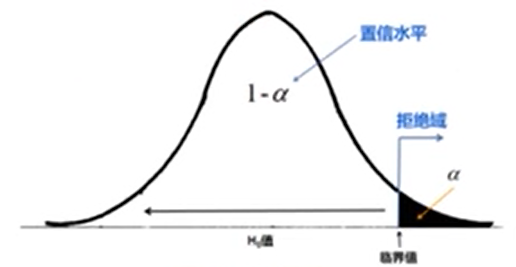
4.2 单侧检验
1.拒绝域在统计分布的一侧,有一个拒绝域,一个临界值,拒绝域的面积为α
五、总体均值的推断
在对总体均值进行推断时,需要考虑总体方差是否已知,用于构造估计量的样本是大样本(通常要求n≥30)还是小样本(n<30)等几种情况
1.α²已知或α²未知大样本
①假定条件
总体服从正态分布,且方差(α²)已知
如果不是正态分布,可由正态分布来近似(n≥30)
②使用正态分布统计量
a、当总体方差α²已知时,符合z分布

b、当α²未知时,用样本方差s²代替,符合t分布
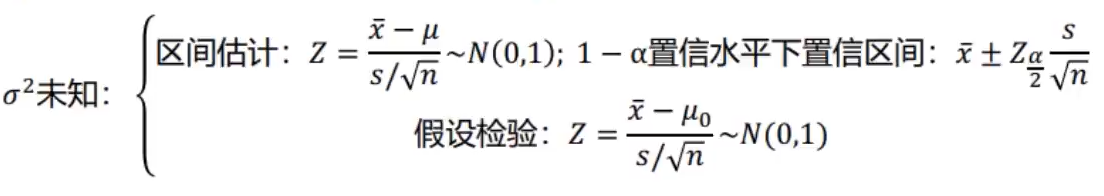
六、练习题
例1:
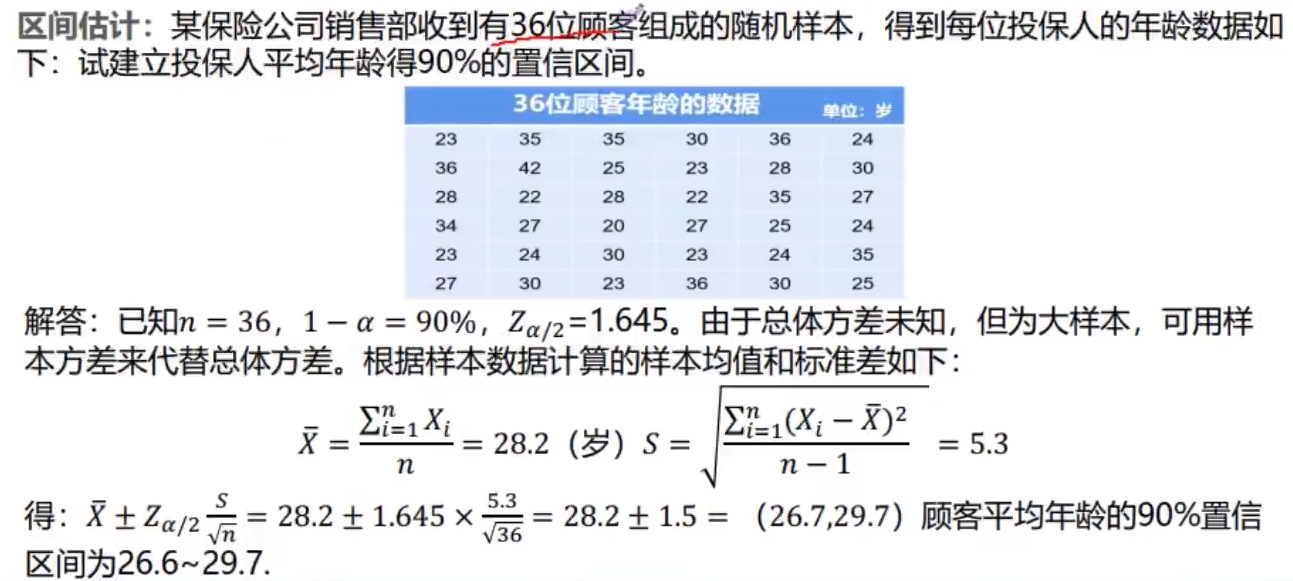
例2:

例3:

版权声明:本文为qq_32833675原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。