matlab如何画曲线的切线_A-12 切线问题中的极限

欢迎光临我的专栏《微积分学习之旅》，一起学习，共同提高。

在前面的文章中，我们主要介绍了函数、它的特点及其种类。从本篇起，我们将把重心移到函数的极限上来。在本篇中我们将知道，当试图找到一条曲线的斜率时，极限是如何产生的。

切线问题（The Tangent Problem）

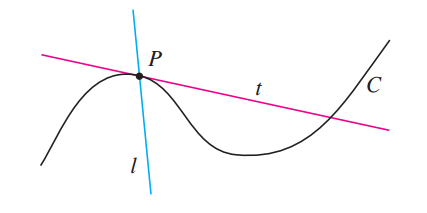
切线（tangent）一词源自拉丁语（tangens），意为“接触”（touching），因此曲线的切线是一条与这条切线相接触的直线。换句话说，一条切线应该与这条曲线在接触点处有相同的方向。可是，我们怎么精确描述这种想法呢？

对于圆的切线，我们可以遵循欧几里得的说法：切线是与圆有且只有一个交点的直线。对于更复杂的曲线，这种定义显得还不充分（inadequate）。例如，下图显示了经过曲线

的交点

的两条直线

和

。直线

只跟曲线

相交一次，但是它与我们感觉中的切线显得不太一样。另一方面，直线

看起来像我们感觉中的切线，可是它却与曲线

相交了两次。

为了更具体地说明这个问题，我们来看看下面这个求抛物线

的切线的例题。

例1 请求出抛物线

在点

处的切线方程。

解答 我们都很清楚，只要知道切线

的斜率

，就可以求出切线方程。困难在于，我们只知道

上的一个点，然而求斜率需要两个点。通过观察我们发现，虽然不能直接求切线

的斜率

，但是我们可以在抛物线上找一个跟

相邻的点

，求得割线 的斜率

，它的值与

比较接近。如下图所示。

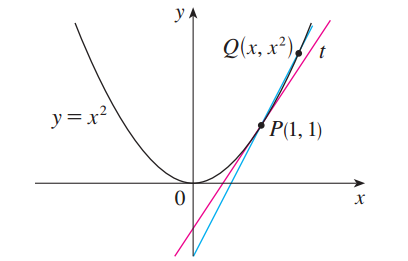
令

，那么

,这样就有

比如令

，那么

下列表格给出了

连续取接近于1的值时，斜率

的结果。随着

越靠近

，

就越趋近1，从表中可以看出，斜率

就越趋近于2。

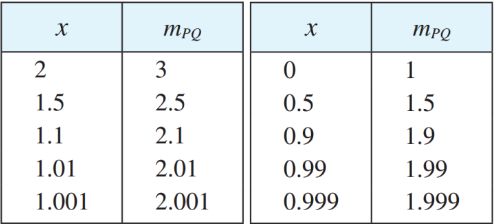
这时我们就说，切线的斜率是割线的斜率的极限，用符号作如下表示

假设切线的斜率就是2，我们用直线方程的点斜式就可以写出过点

的切线方程为

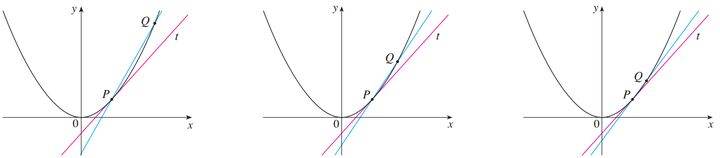
下图展示了

沿着抛物线靠近

的过程，相应的割线绕着

点旋转到趋近于切线

。

在科学研究中的很多函数其实并非显性的或直接给出的，而是由实验数据模拟得到的。下面的例子展示了如何估算一个函数图像的切线斜率。

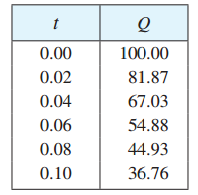
例2相机上的闪光灯是这样工作的。先在电容器上储存电荷，然后在触发闪光灯时迅速释放出电荷。下列数据表描述了电容器上留存的电荷量

（微库仑）在闪光之后随时间

(秒)变化的情况。利用表中数据画出函数图像，并估算在

时的切线斜率。（注意：这里斜率表示从电容器流向闪光灯泡的电流强度）

解答 在下图中，我们描出了散点图，并用它们画出了函数的拟合曲线。

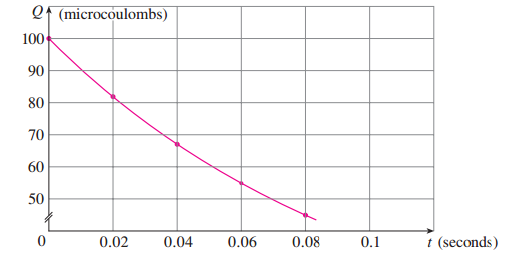
从图中找出两点

和

，那么割线

的斜率是

对于其它过

的割线，采用相似的计算方法得到了下表。

从表中我们可以认为，

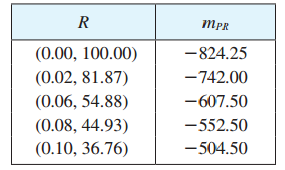
时的切线斜率应该处于-742到-607.5之间，在最近的两条割线之间的斜率平均值为

所以通过这种方法， 我们估计这条切线的斜率约等于-675。

另一种求斜率的方法如下图所示，画出P的近似切线，并作出三角形ABC.

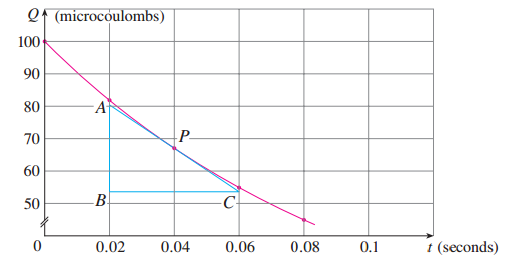
这样斜率就可以用下面的计算方法得出。

小结

在本篇中，我们详细介绍了通过极限的思想求切线斜率的方法。在下一篇我们将会看到切线斜率问题在求解瞬时速度方面的应用。

本篇到此结束，感谢您的阅读。

本专栏最新目录请参阅：

（如果您喜欢本专栏，请点击关注；如果认可我的笔记，也请点个赞同呗）