目录
一、什么是分治（what？）
分治，即分而治之。这是一种将大规模问题分解为若干个规模较小的相同子问题，进而求得最终结果的一种策略思想。
二、为什么要分治（why? ）
当一个问题规模较大，且
（1）原问题可分为若干个规模较小的子问题。
（2）子问题相互独立。
（3）子问题的解可以合并为原问题的解。
这时使用分治算法能更好的解决问题。
三、怎么使用分治（how？）
分治的步骤一般如下：
（1）分解：将要解决的问题分解为若干个规模较小、相互独立、与原问题形式相同的子问题。
（2）治理：求解各个子问题。由于各个子问题与原问题形式相同，只是规模小而已，而当子问题划分得足够小时，就可以用较简单的方法解决。
（3）合并：按原问题的要求，将子问题的解逐层合并成原问题的解。
就是化整为零，在化零为整的过程。
在分治中，递归是一把利器。
四、典型例题分析：
例题1：猜数字游戏--二分搜索技术
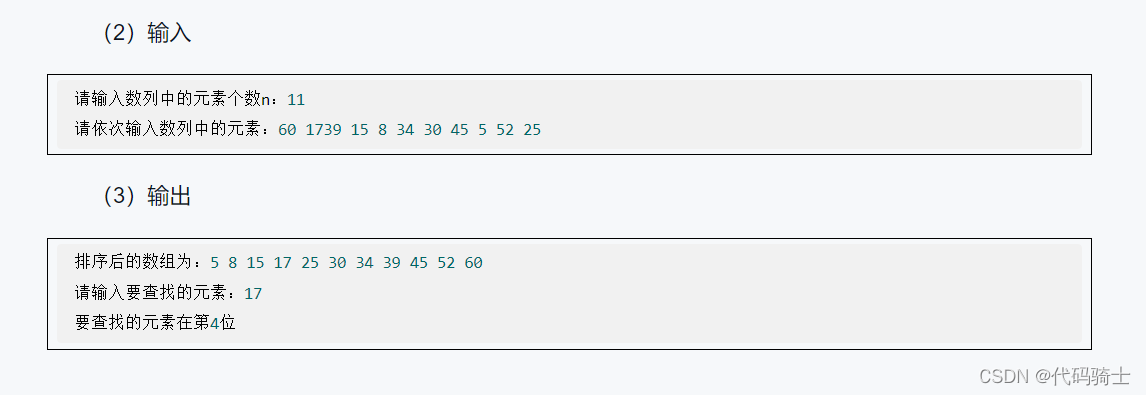
问题分析：
在最坏的情况，需要猜n次才能得出答案，但是由于0~10是一串有序的数，我们没必要一个一个去猜，可以从中间开始向两边搜索，这样可以大大提高寻找效率。所以这里要介绍一种新的查找方法——折半查找。当我们的面对的数据是有序序列时，就可以使用这种策略。
算法设计：
问题简化：
给定n个元素，这些元素是有序的（假设为升序），从中查找指定元素x。
算法思想：
将有序列分成两部分，将待查元素与中间值进行比较，如果相等，返回中间值；若果小于中间值，那么将原序列的右半部分切掉，将x和左边序列的中间值比较，再重复以上判定。
算法设计：
用一维数组s[]存储有序序列，设变量low和high表示查找范围的下界和上界，mid表示查找范围的中间位置，x为特定待查值。
（1）初始化。令low=0，即指向有序数列的第一个元素，high = n - 1，指有序数列的最后一个元素。mid指向中间值 （high-low）/2+low 或者 ( high+low)/2
（2）判定关系若low<=high，则判断x和s[mid]的大小关系，如果x>s[mid],low = mid+1,更新中间值mid = (low+high)/2；如果x<s[mid],high=mid-1,更新中间值mid = (low+high)/2。若果x==s[mid],返回mid就是x的位置。
（3）如果low>high,说明数据错误，待查值不存在。
图解算法：
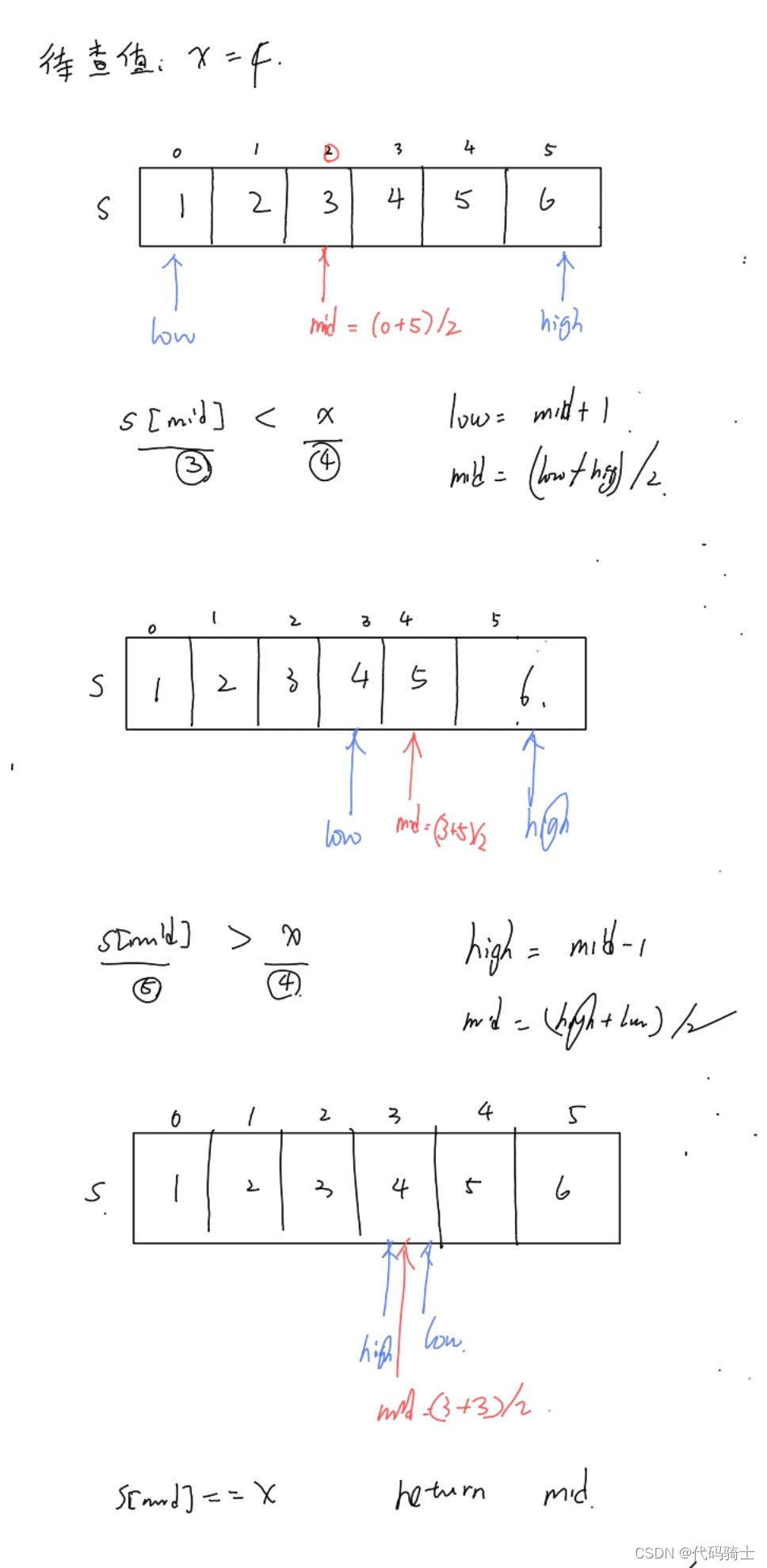
伪代码：
二分搜索：
int BinarySearch(int n,int s[],int x)
{
int low=0,high=n-1;
while(low<=high)
{
int mid=(high-low)/2+low;
if(x==s[mid])
{
return mid;
}
else if(x<s[mid])
{
high=mid-1;
}
else if(x>s[mid])
{
low=mid+1;
}
}
return -1;//返回-1没找到x
}实战代码：
#include<iostream>
#include<algorithm>
using namespace std;
const int M=10000;
int x,n,i;
int s[M];
int BinarySearch(int n,int s[],int x)
{
int low=0,high=n-1;
while(low<=high)
{
int mid=(high-low)/2+low;
if(x==s[mid])
{
return mid;
}
else if(x<s[mid])
{
high=mid-1;
}
else
{
low=mid+1;
}
}
return -1;//返回-1没找到x
}
int main()
{
cout<<"请输入数列中的元素："<<endl;
while(cin>>n)
{
cout<<"请依次输入列表中元素：";
for(int i=0; i < n; i++)
{
cin>>s[i];
}
sort(s,s+n);
cout<<"排列后的数组为：";
for(int i=0; i < n; i++)
{
cout<<s[i]<<' ';
}
cout<<endl;
cout<<"请输入要查元素：";
cin>>x;
i = BinarySearch(n,s,x);
if(i==-1) cout<<"该数列中没有待查值。"<<endl;
else cout<<"已查到的元素在"<<i<<"位"<<endl;
}
return 0;
}
算法复杂度分析：
例题2：合久必分，分久必合--合并排序
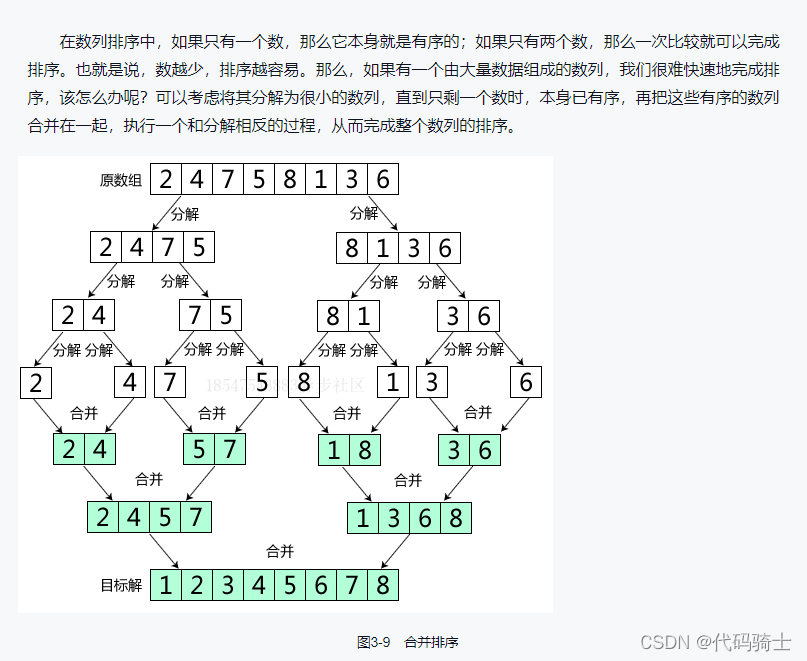
问题分析：
显然，合并排序采用的策略就是分治。将一个给定的无序数列，分解成两个规模大致相同的子序列，然后将两个子序列进行排序和合并。如果面对的问题不易解决就继续将子序列在分，直到分解成单个元素为一个子序列，这是每一个序列都可以当做是一个排好的子序列，然后在进行合并，得到一个完整的序列。
算法设计：
合并排序采用分治策略实现对n个元素进行排序的算法，是分治法的一个典型应用和完美体现。他是一种平衡、简单的二分分治策略。过程大致如下：
（1）分解——将待排序列元素分成大小大致相同的两个子序列。
（2）治理——对两个子序列进行合并排序。
（3）合并——将排好序的有序子序列进行合并，得到最终的有序序列。
算法图解：
伪代码：
（1）合并算法：
void Merge(int A[],int low,int mid,int high)
{
int *B = new int[high-low+1];
int i = low,j = mid+1,k = 0;
while(i<=mid&&j<=high)
{
if(A[i]<=A[j])
B[k++]=A[i++];//这里是先对数组赋值，再移动指针
else
B[k++]=A[j++];
}
//如果前一半剩余
while(i<=mid)
{
B[k++]=A[i++];
}
//如果后一半有剩余
while(j<=high)
{
B[k++]=A[j++];
}
//将合并的序列赋值给A数组
for(i = low,k=0; i <= high; i++)
{
A[i] = B[k++];
}
}（2）分治算法（递归）
void MergeSort(int A[],int low, int high)
{
if(low<high)
{
int mid = (low+high)/2;
MergeSort(A,low,mid);//左边拆分
MergeSort(A,mid+1,high);//右边拆分
Merge(A,low,mid,high);//分久必合
}
}实战代码：
#include<iostream>
using namespace std;
void Merge(int A[],int low,int mid,int high)
{
int *B = new int[high-low+1];
int i = low,j = mid+1,k = 0;
while(i<=mid&&j<=high)
{
if(A[i]<=A[j])
B[k++]=A[i++];//这里是先对数组赋值，再移动指针
else
B[k++]=A[j++];
}
//如果前一半剩余
while(i<=mid)
{
B[k++]=A[i++];
}
//如果后一半有剩余
while(j<=high)
{
B[k++]=A[j++];
}
//将合并的序列赋值给A数组
for(i = low,k=0; i <= high; i++)
{
A[i] = B[k++];
}
}
void MergeSort(int A[],int low, int high)
{
if(low<high)
{
int mid = (low+high)/2;
MergeSort(A,low,mid);//左边拆分
MergeSort(A,mid+1,high);//右边拆分
Merge(A,low,mid,high);//分久必合
}
}
int main()
{
int n, A[100];
cout<<"请输入数列中的元素个数n为："<<endl;
cin>>n;
cout<<"请依次输入数列中的元素："<<endl;
for(int i=0; i<n; i++)
cin>>A[i];
MergeSort(A,0,n-1);
cout<<"合并排序结果："<<endl;
for(int i=0;i<n;i++)
cout<<A[i]<<" ";
cout<<endl;
return 0;
}
算法复杂度：
例题3：兵贵神速--快速排序
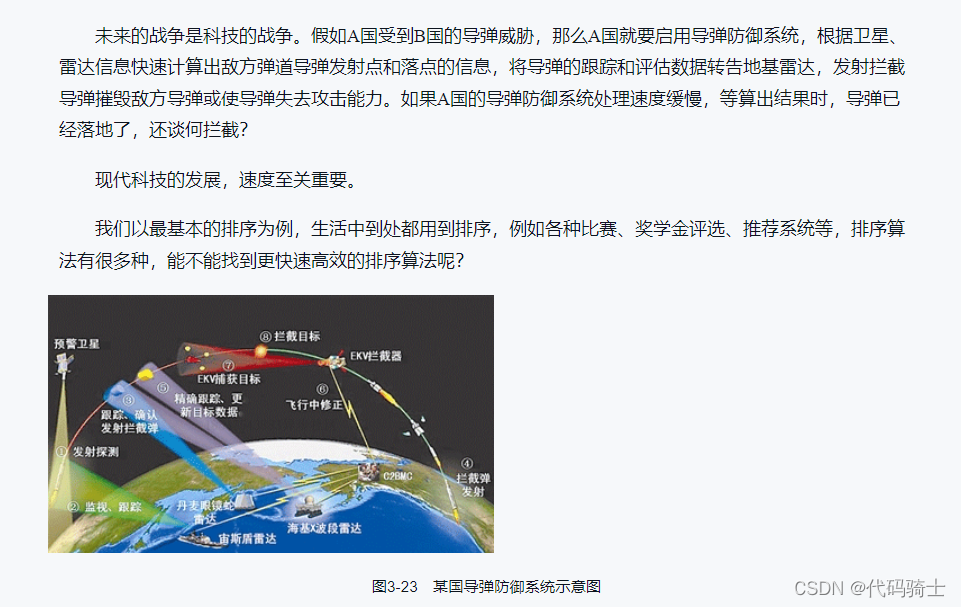
问题分析：
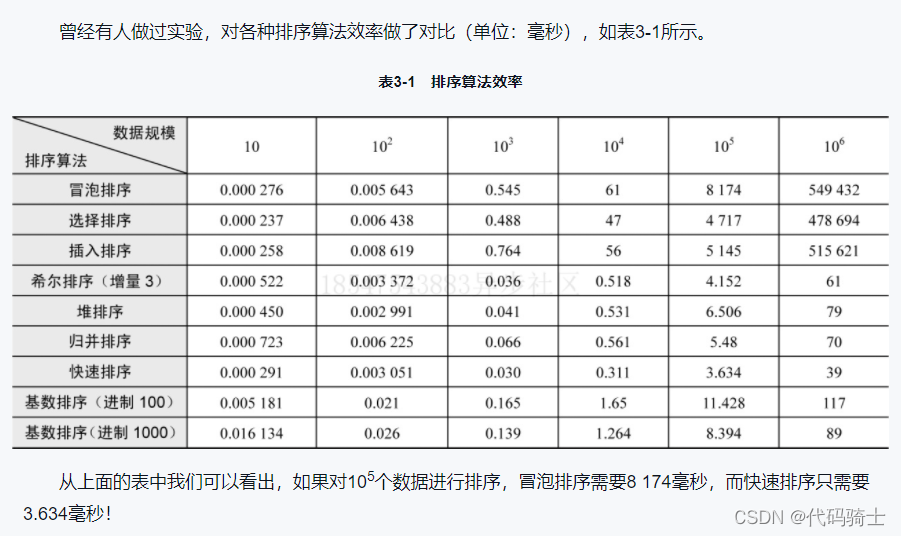
算法设计：
快速排序的基本思想也是分治。
（1）分解：先从数列中选取一个元素作为基准。以基准元素为标准。比基准元素小的值放在基准元素左边，比基准元素大的值放在基准元素右边。
（2）治理：对两个子序列进行快速排序。
（3）合并：将两个排好的序列合在一起，得到原问题的解。
图解算法：
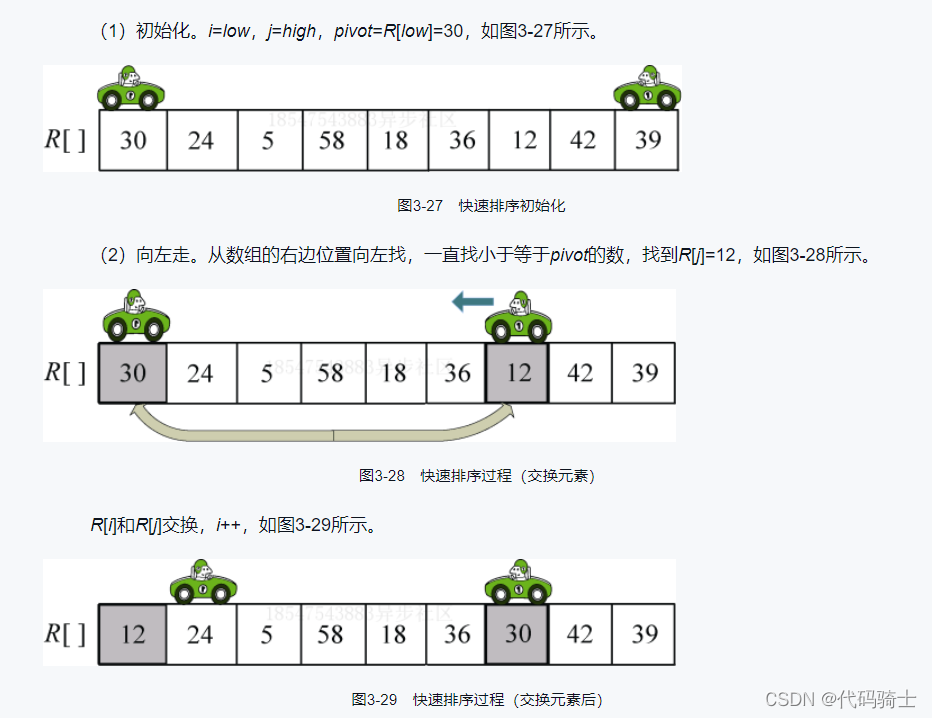
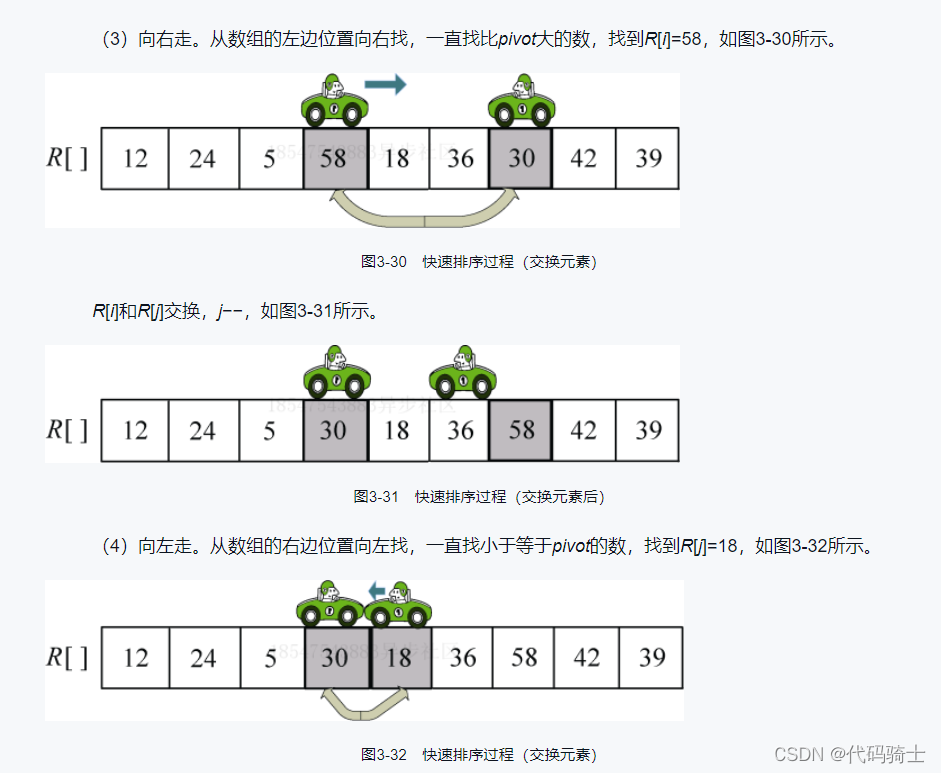
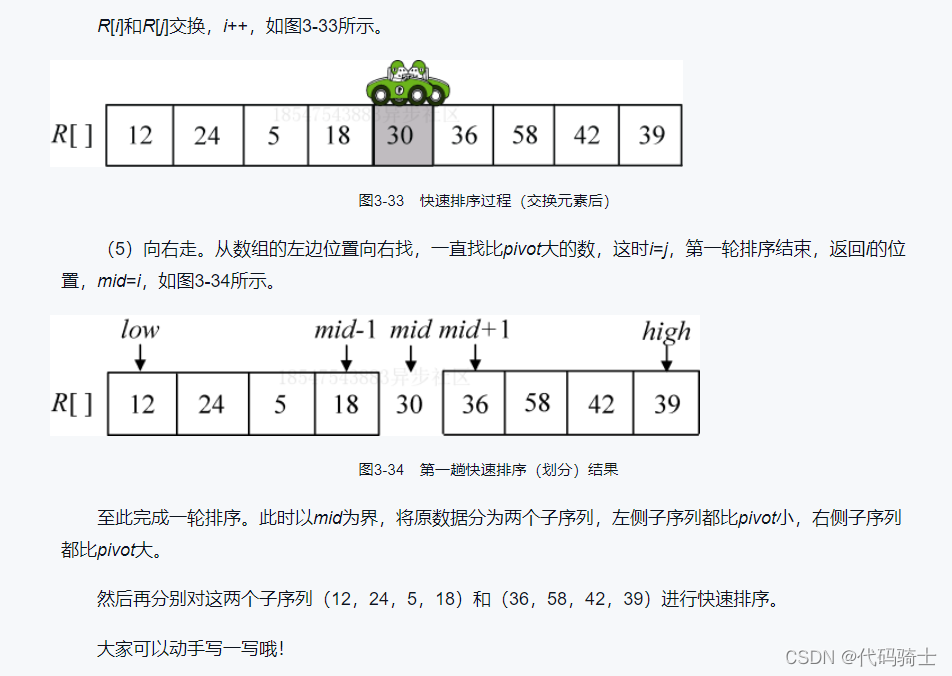
伪代码：
（1）划分函数
int Partition(int r[],int low,int high) //划分函数
{
int i=low,j=high,pivot=r[low]; //基准元素
while(i<j)
{
while(i<j&&r[j]>pivot)
j--; //向左扫描
if(i<j)
{
swap(r[i++],r[j]); //r[i]和r[j]交换后i右移一位
}
while(i<j&&r[i]<=pivot)
i++; //向右扫描
if(i<j)
{
swap(r[i],r[j--]); //r[i]和r[j]交换后j左移一位
}
}
return i; //返回最终划分完成后基准元素所在的位置
} （2）快速排序递归 
void QuickSort(int R[],int low,int high){
int mid;
if(low<high)
{
mid=Partition(R,low,high); //返回基准元素位置
QuickSort(R,low,mid-1); //左区间递归快速排序
QuickSort(R,mid+1,high); //右区间递归快速排序
}
}实战代码：
#include <iostream>
using namespace std;
int Partition(int r[],int low,int high) //划分函数
{
int i=low,j=high,pivot=r[low]; //基准元素
while(i<j)
{
while(i<j&&r[j]>pivot) j--; //向左扫描
if(i<j)
{
swap(r[i++],r[j]); //r[i]和r[j]交换后i右移一位
}
while(i<j&&r[i]<=pivot) i++; //向右扫描
if(i<j)
{
swap(r[i],r[j--]); //r[i]和r[j]交换后j左移一位
}
}
return i; //返回最终划分完成后基准元素所在的位置
}
void QuickSort(int R[],int low,int high)//快速排序递归算法
{
int mid;
if(low<high)
{
mid=Partition(R,low,high); //基准位置
QuickSort(R,low,mid-1); //左区间递归快速排序
QuickSort(R,mid+1,high); //右区间递归快速排序
}
}
int main()
{
int a[1000];
int i,N;
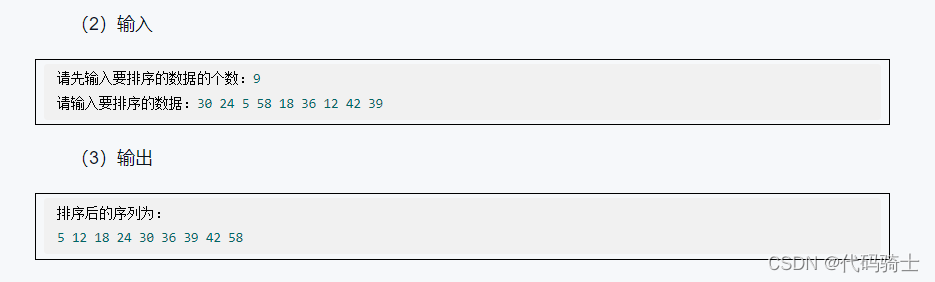
cout<<"请先输入要排序的数据的个数：";
cin>>N;
cout<<"请输入要排序的数据：";
for(i=0;i<N;i++)
cin>>a[i];
cout<<endl;
QuickSort(a,0,N-1);
cout<<"排序后的序列为："<<endl;
for(i=0;i<N;i++)
cout<<a[i]<<" " ;
cout<<endl;
return 0;
}例题4：效率至上--大整数乘法
问题分析：
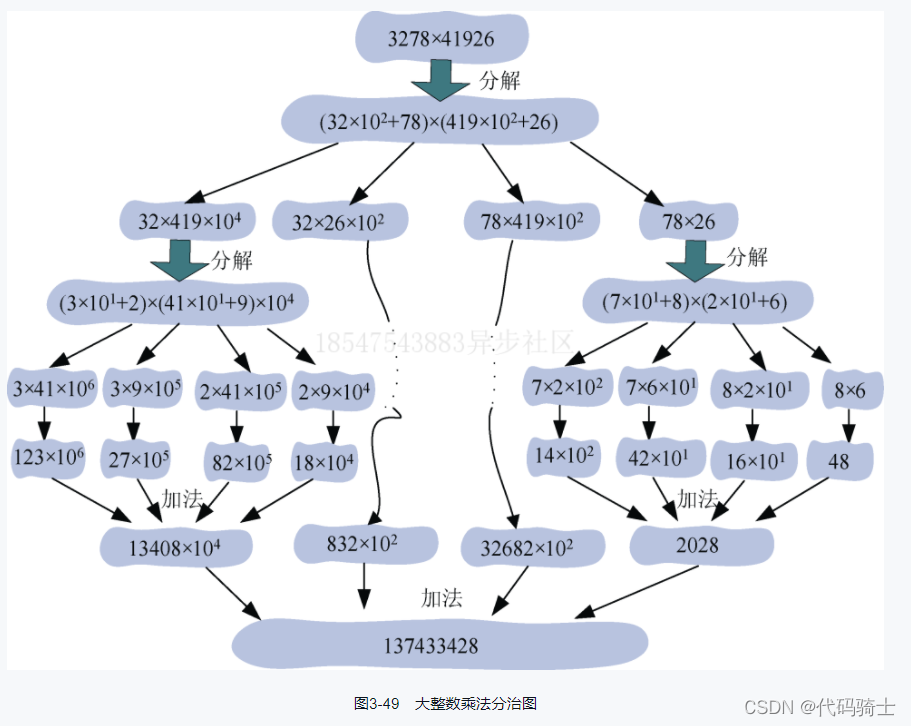
算法设计：
图解算法：
道理都懂，那么具体应该如何操作？
首先将两个大整数以字符串形式输入，
转换成数字后，倒序存储在s[]中，
l 表示数的长度，
c 表示数的次幂。
两个大数的初始次幂是0.
(1)初始化
（2）分解
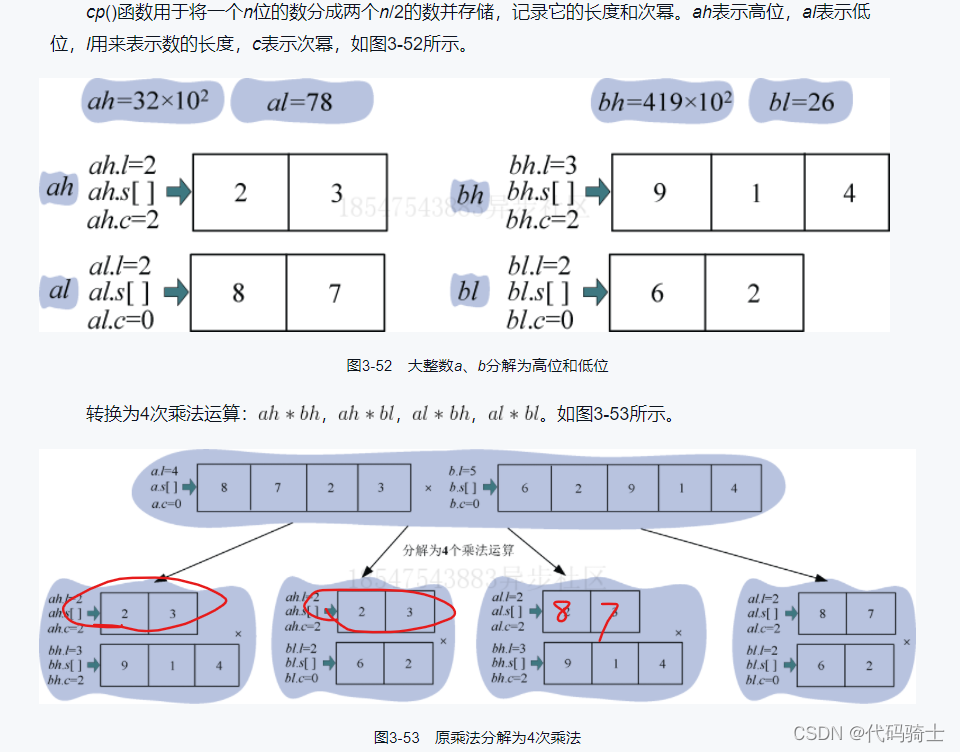
（3）求解子问题
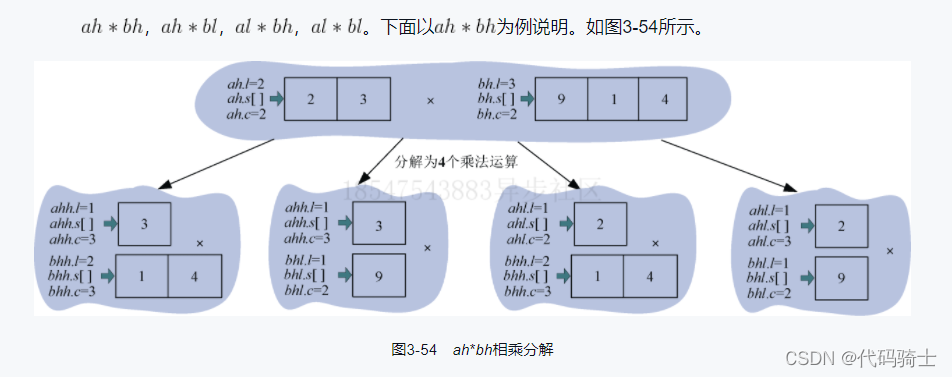
(4)继续求解子问题
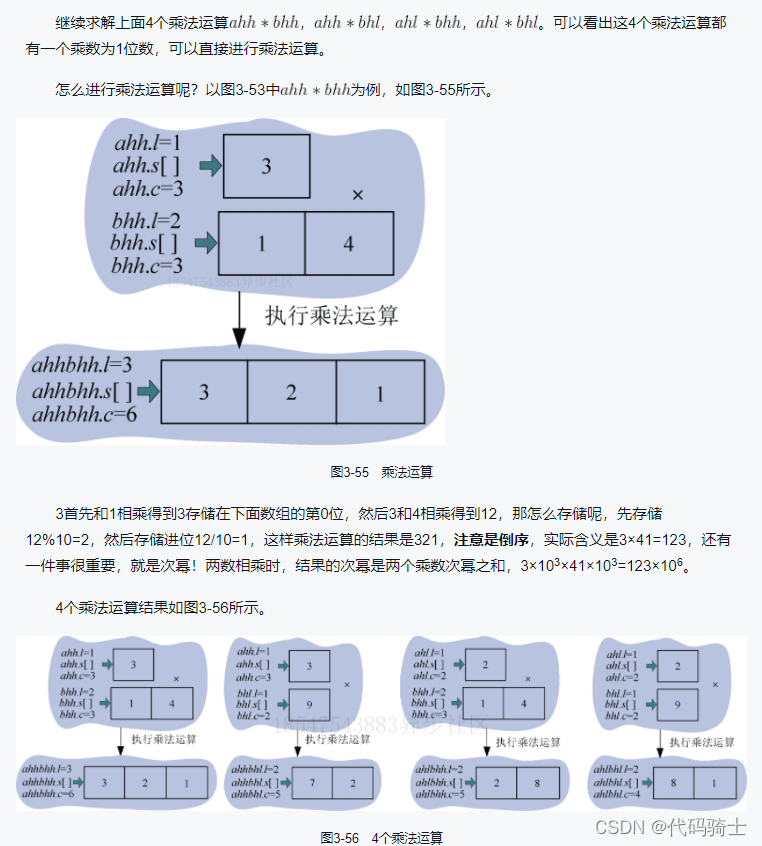
（5）合并
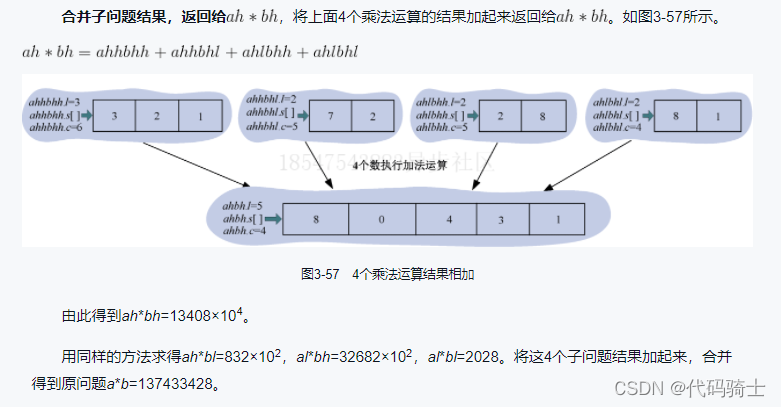
伪代码：
（1）数据结构
将两个大数以字符串的形式输入，然后定义结构体Node，其中：
s[]存储大数倒序，l 表示长度，c 表示次幂。两个大数的初始次幂为0.
char sa[10000];//接收大数的字符串
char sb[10000];//接收大数的字符串
typedef struct _Node{
int s[M];//数组，倒序存储大数
int l;//代表数的长度
int c;//代表数的次幂
}Node,*pNode;
（2）划分函数
其中，cp（）函数用于将一个n位的数分成两个n/2的数并储存，纪录它的次幂。
void cp(pNode*src,pNode*des,int st,int l)
{
//src表示分解的数结点，des表示分解后得到的数结点
//st表示从src结点数组中取数的开始位置，1表示取数的长度
int i,j;
for(i = st,j=0;i<st+l;i++,j++)
{
des->s[j] = src->s[i];
}
des->l = l;//长度等于取数的长度
des->c = st+src->c;//des次幂等于开始取数的位置加上src
} 举例：如果有大数43579，我们应该把数放在结点a中
ma = a.l/2; //ma表示a长度的一半，此例中a.l=5，ma=2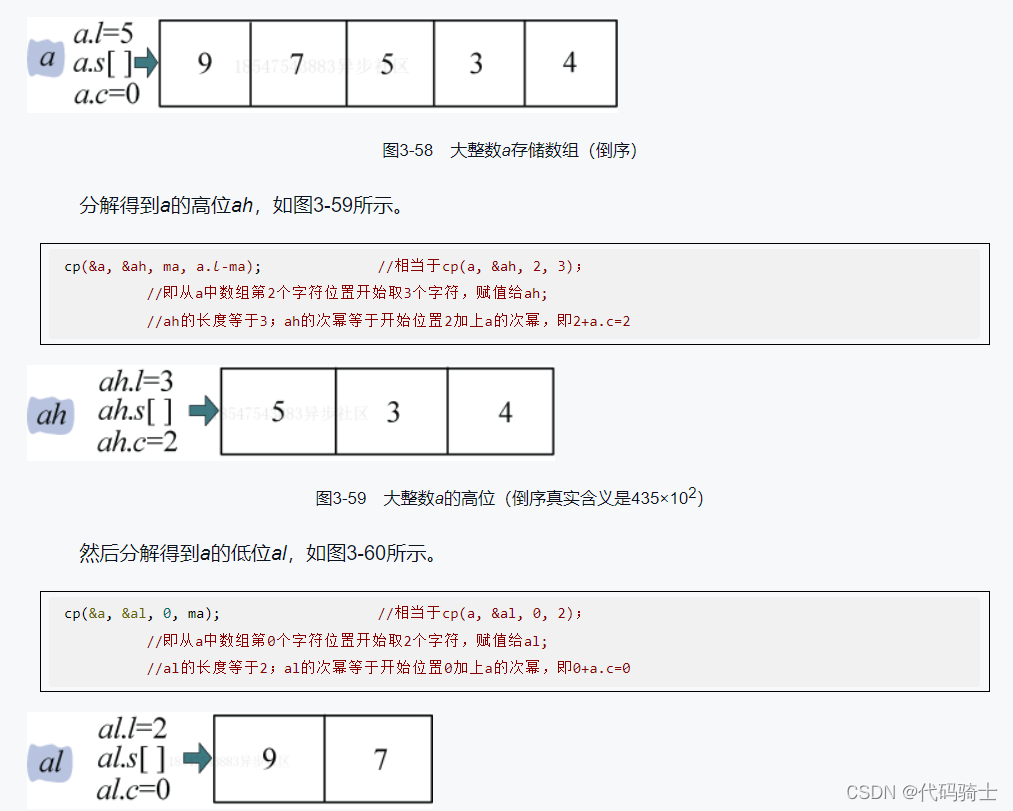
这样两次调用cp（）函数，我们就把一个大的整数分解成了两个长度约为原来一半的整数。
（3）乘法运算
定义mul函数用于将两数相乘，不断分解，直到有一个乘数为1时停止，让这两个数相乘，并记录结果回溯。
ma = pa->l/2; //ma表示a长度的一半
mb = pb->l/2; //mb表示b长度的一半
if(!ma || !mb) //如果!ma说明ma=0，即a的长度为1，该乘数为1位数
//如果!mb说明mb=0，即b的长度为1，该乘数为1位数
{
if(!ma) //!ma说明a为1位数，a、b交换，保证a的长度大于等于b的长度
{
temp =pa;
pa = pb;
pb = temp;
} //交换后b的长度为1
ans->c = pa->c + pb->c; //结果的次幂等于两乘数次幂之和
w = pb->s[0];//因为交换后b的长度为1，用变量 w记录即可
cc= 0; //初始化进位cc为0
for(i=0; i <pa->l; i++) //把a中的数依次取出与w相乘，记录结果和进位
{
ans->s[i] = (w*pa->s[i] + cc)%10;//存储相乘结果的个位，十位做进位处理
cc = (w*pa->s[i] + cc)/10; //处理进位
}
（4）合并函数
add（）函数将分解得到的数进行相加合并。
void add(pNode pa, pNode pb, pNode ans)
{ //程序调用时把 a、b地址传递给pa、pb参数，表示待合并的两个数
//ans记录它们相加的结果
int i, cc, k,alen,blen,len;
int ta, tb; //ta、tb分别记录a、b相加时对应位上的数
pNode temp;
if(pa->c <pb->c) //交换以保证a的次幂大
{
temp = pa;
pa = b;
pb =temp;
}
ans->c = pb->c; //结果的次幂为两个数中小的次幂
cc = 0; //初始化进位cc为0
k=pa->c - pb->c //k为a左侧需要补零的个数 
alen=pa->l + pa->c; //a数加上次幂的总长度，上例中alen=6
blen=pb->l + pb->c; //b数加上次幂的总长度，上例中alen= 5
if(alen>blen)
len=alen; //取a、b总长度的最大值
else
len=blen;
len=len-pb->c; //结果的长度为a，b之中的最大值减去最低次幂，上例中len= 4
//最低次幂是不进行加法运算的位数)
for(i=0; i<len; i++)
{
if(i <k) //k为a左侧需要补零的个数
ta = 0; //a左侧补零
else
ta =pa->s[i-k];//i=k时，补0结束，从a数组中第0位开始取数字
if(i <b->l)
tb = pb->s[i]; //从b数组中第0位开始取数字
else
tb = 0; //b数字先取完，b右侧补0
if(i>=pa->l+k) //a数字先取完，a右侧补0
ta = 0;
ans->s[i] = (ta + tb + cc)%10; //记录两位之和的个位数，十位做进位处理
cc = (ta + tb + cc)/10;
} 
实战代码：
//program 3-4
#include <stdlib.h>
#include <cstring>
#include <iostream>
using namespace std;
#define M 100
char sa[1000];
char sb[1000];
typedef struct _Node
{
int s[M];
int l; //代表字符串的长度
int c;
} Node,*pNode;
void cp(pNode src, pNode des, int st, int l)
{
int i, j;
for(i=st, j=0; i<st+l; i++, j++)
{
des->s[j] = src->s[i];
}
des->l = l;
des->c = st + src->c; //次幂
}
void add(pNode pa, pNode pb, pNode ans)
{
int i,cc,k,palen,pblen,len;
int ta, tb;
pNode temp;
if((pa->c<pb->c)) //保证Pa的次幂大
{
temp = pa;
pa = pb;
pb = temp;
}
ans->c = pb->c;
cc = 0;
palen=pa->l + pa->c;
pblen=pb->l + pb->c;
if(palen>pblen)
len=palen;
else
len=pblen;
k=pa->c - pb->c;
for(i=0; i<len-ans->c; i++) //结果的长度最长为pa，pb之中的最大长度减去最低次幂
{
if(i<k)
ta = 0;
else
ta = pa->s[i-k]; //次幂高的补0，大于低的长度后与0进行计算
if(i<pb->l)
tb = pb->s[i];
else
tb = 0;
if(i>=pa->l+k)
ta = 0;
ans->s[i] = (ta + tb + cc)%10;
cc = (ta + tb + cc)/10;
}
if(cc)
ans->s[i++] = cc;
ans->l = i;
}
void mul(pNode pa, pNode pb, pNode ans)
{
int i, cc, w;
int ma = pa->l>>1, mb = pb->l>>1; //长度除2
Node ah, al, bh, bl;
Node t1, t2, t3, t4, z;
pNode temp;
if(!ma || !mb) //如果其中个数为1
{
if(!ma) //如果a串的长度为1，pa,pb交换，pa的长度大于等于pb的长度
{
temp = pa;
pa = pb;
pb = temp;
}
ans->c = pa->c + pb->c;
w = pb->s[0];
cc = 0; //此时的进位为c
for(i=0; i < pa->l; i++)
{
ans->s[i] = (w*pa->s[i] + cc)%10;
cc= (w*pa->s[i] + cc)/10;
}
if(cc)
ans->s[i++] = cc; //如果到最后还有进位，则存入结果
ans->l = i; //记录结果的长度
return;
}
//分治的核心
cp(pa, &ah, ma, pa->l-ma); //先分成4部分al,ah,bl,bh
cp(pa, &al, 0, ma);
cp(pb, &bh, mb, pb->l-mb);
cp(pb, &bl, 0, mb);
mul(&ah, &bh, &t1); //分成4部分相乘
mul(&ah, &bl, &t2);
mul(&al, &bh, &t3);
mul(&al, &bl, &t4);
add(&t3, &t4, ans);
add(&t2, ans, &z);
add(&t1, &z, ans);
}
int main()
{
Node ans,a,b;
cout << "输入大整数 a："<<endl;
cin >> sa;
cout << "输入大整数 b："<<endl;
cin >> sb;
a.l=strlen(sa); //sa,sb以字符串进行处理
b.l=strlen(sb);
int z=0,i;
for(i = a.l-1; i >= 0; i--)
a.s[z++]=sa[i]-'0'; //倒向存储
a.c=0;
z=0;
for(i = b.l-1; i >= 0; i--)
b.s[z++] = sb[i]-'0';
b.c = 0;
mul(&a, &b, &ans);
cout << "最终结果为：";
for(i = ans.l-1; i >= 0; i--)
cout << ans.s[i]; //ans用来存储结果，倒向存储
cout << endl;
return 0;
}