图是一种数据结构,其中节点可以具有零个或多个相邻元素。两个节点之间的连接称为边。节点也可以称为顶点。
图分为三种:无向图、有向图、带权图
图的表示方式有两种:二维数组表示(邻接矩阵);链表表示(邻接表)
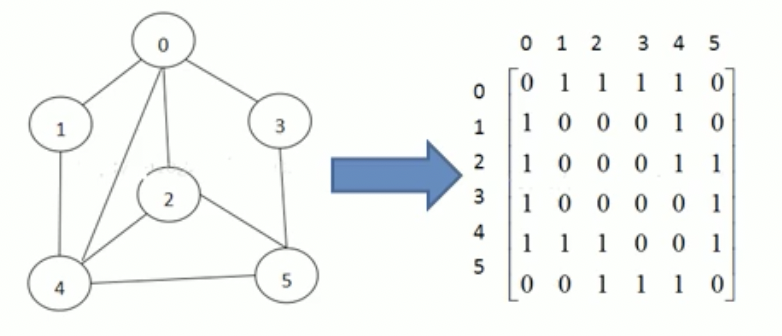
邻接矩阵
邻接矩阵是表示图形中顶点之间相邻关系的矩阵,对于n个顶点的图而言,矩阵的行和列表示的是1……n个点。邻接矩阵需要为每个顶点都分配n个边的空间,其实有很多边都是不存在的,会造成空间的一定损失。
邻接表
连接表的实现只关心存在的边,不关心不存在的边。因此没有空间浪费,邻接表由数组+链表组成
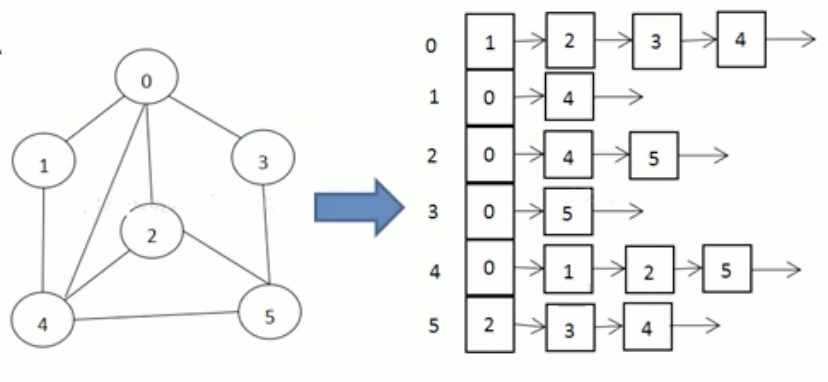
说明:
标号为0的节点的相关联的节点为1,2,3,4
标号为1的节点为0,4
标号为2的节点的相关联的节点为0,4,5
……
代码实现图结构
/**
* 邻接矩阵表示图
* @author sixiaojie
* @date 2022-01-07-19:05
*/
public class Graph {
/** 存储顶点集合 */
private ArrayList<String> vertexList;
/** 存储图对应的邻接矩阵 */
private int[][] edges;
/** 表示边的数目 */
private int numOfEdges;
public static void main(String[] args) {
// 顶点个数
int n = 5;
String[] vertexs = {"A","B","C","D","E"};
Graph graph = new Graph(n);
// 添加顶点
for (String vertexValue : vertexs) {
graph.insertVertex(vertexValue);
}
// 添加边 A-B A-C B-C B-D B-E
graph.insertEdge(0,1,1);// A-B
graph.insertEdge(0,2,1);// A-C
graph.insertEdge(1,2,1);// B-C
graph.insertEdge(1,3,1);// B-D
graph.insertEdge(1,4,1);// B-E
// 显示
graph.showGraph();
}
/**
* 构造器
*/
public Graph(int n) {
// 初始化矩阵和vertexList
edges = new int[n][n];
vertexList = new ArrayList<String>(n);
numOfEdges = 0;
}
/**
* 插入顶点
* @param vertex
*/
public void insertVertex(String vertex){
vertexList.add(vertex);
}
/**
* 添加边
* @param v1 第一个顶点对应的下标
* @param v2 第二个顶点对应的下标
* @param weight 权值
*/
public void insertEdge(int v1,int v2,int weight){
edges[v1][v2] = weight;
edges[v2][v1] = weight;
numOfEdges ++ ;
}
/**
* 返回顶点个数
* @return
*/
public int getNumOfVertex(){
return vertexList.size();
}
/**
* 返回边的数目
* @return
*/
public int getNumOfEdges(){
return numOfEdges;
}
/**
* 返回顶点i(下标)对应的数据0->'A',1->'B',2->'C'
* @param index
* @return
*/
public String getValueByIndex(int index){
return vertexList.get(index);
}
/**
* 返回v1,v2的权值
* @param v1
* @param v2
* @return
*/
public int getWeiht(int v1, int v2){
return edges[v1][v2];
}
/**
* 显示对应的矩阵
*/
public void showGraph(){
for (int[] link : edges) {
System.out.println(Arrays.toString(link));
}
}
}图的遍历
图的遍历是指,从给定图中任意指定的顶点(称为初始点)出发,按照某种搜索方法沿着图的边访问图中的所有顶点,使每个顶点仅被访问一次。遍历过程中得到的顶点序列称为图遍历序列。
图的遍历过程中,根据搜索方法的不同,又可以划分为两种搜索策略:
深度优先搜索
广度优先搜索
深度优先搜索(DFS,Depth First Search)
深度优先搜索,从起点出发,从规定的方向中选择其中一个不断地向前走,直到无法继续为止,然后尝试另外一种方向,直到最后走到终点。就像走迷宫一样,尽量往深处走。
DFS 解决的是连通性的问题,即,给定两个点,一个是起始点,一个是终点,判断是不是有一条路径能从起点连接到终点。
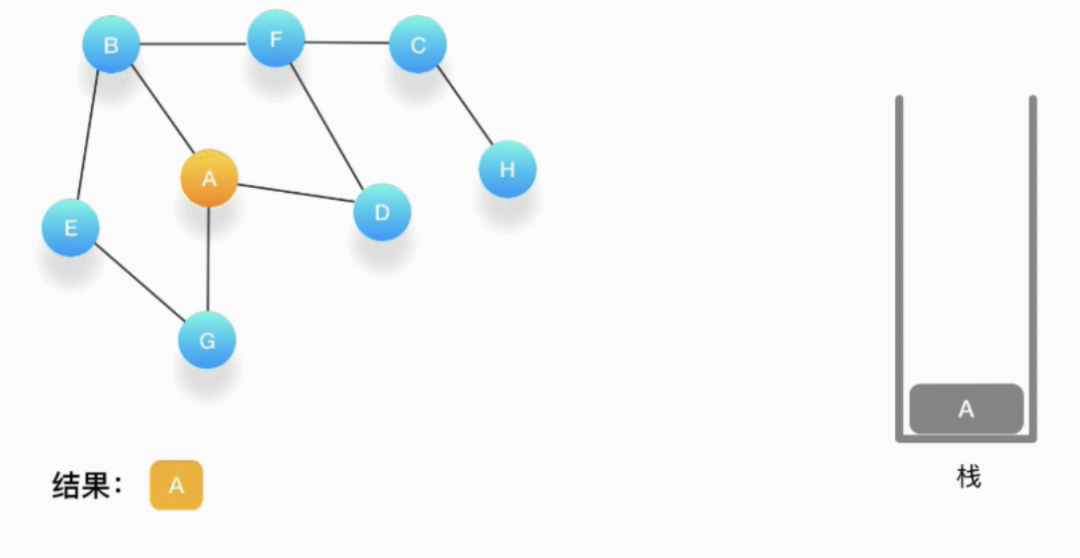
假设我们有这么一个图,里面有A、B、C、D、E、F、G、H 8 个顶点,点和点之间的联系如下图所示, 对这个图进行深度优先的遍历。

依赖栈(Stack),特点是后进先出(LIFO)。
第一步,选择一个起始顶点,例如从顶点 A 开始。把 A 压入栈,标记它为访问过(用红色标记),并输出到结果中。
第二步,寻找与 A 相连并且还没有被访问过的顶点,顶点 A 与 B、D、G 相连,而且它们都还没有被访 问过,我们按照字母顺序处理,所以将 B 压入栈,标记它为访问过,并输出到结果中。
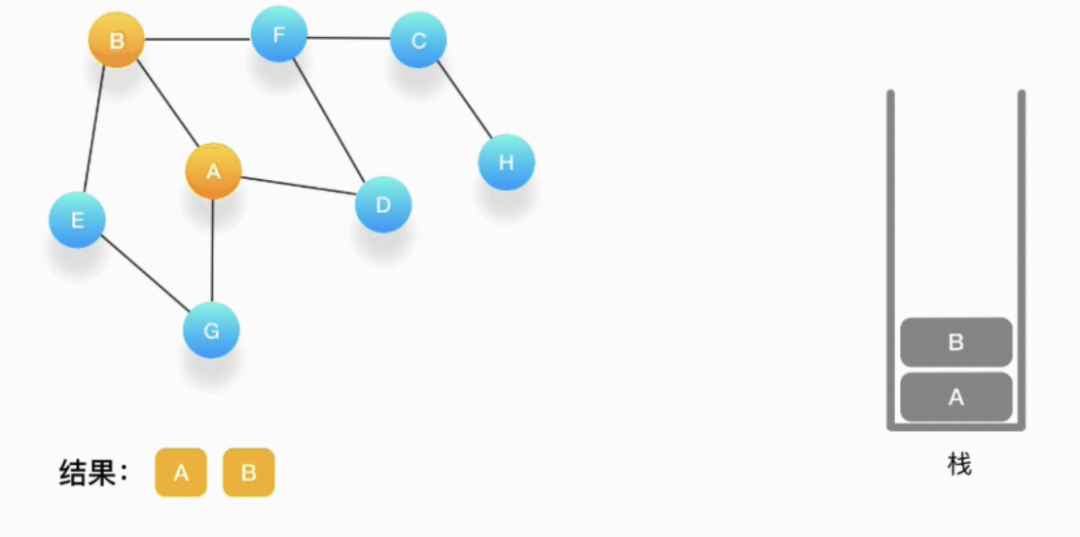
第三步,现在我们在顶点 B 上,重复上面的操作,由于 B 与 A、E、F 相连,如果按照字母顺序处理的话,A 应该是要被访问的,但是 A 已经被访问了,所以我们访问顶点 E,将 E 压入栈,标记它为访问过,并输出到结果中。
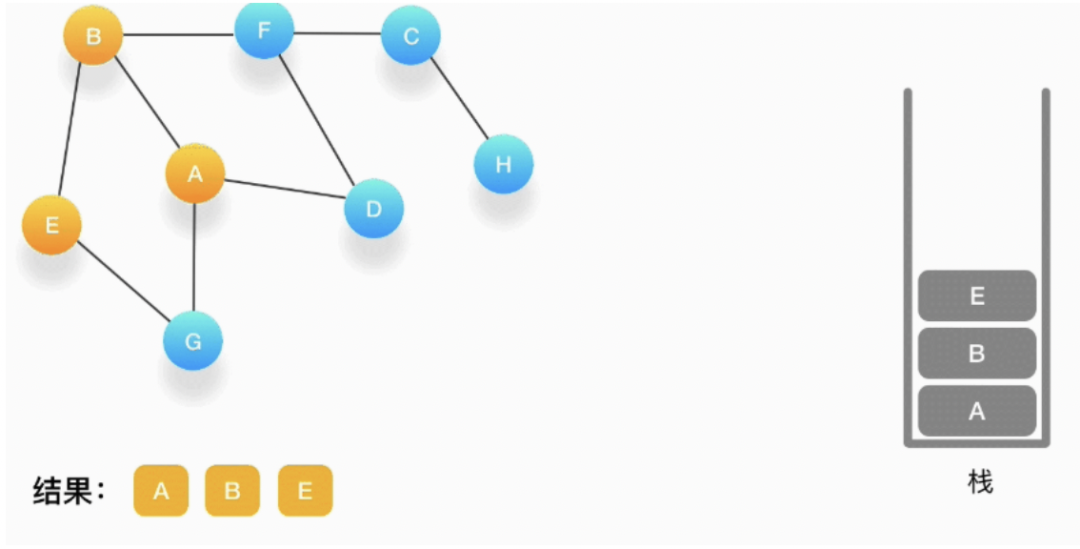
第四步,从 E 开始,E 与 B、G 相连,但是B刚刚被访问过了,所以下一个被访问的将是G,把G压入 栈,标记它为访问过,并输出到结果中。
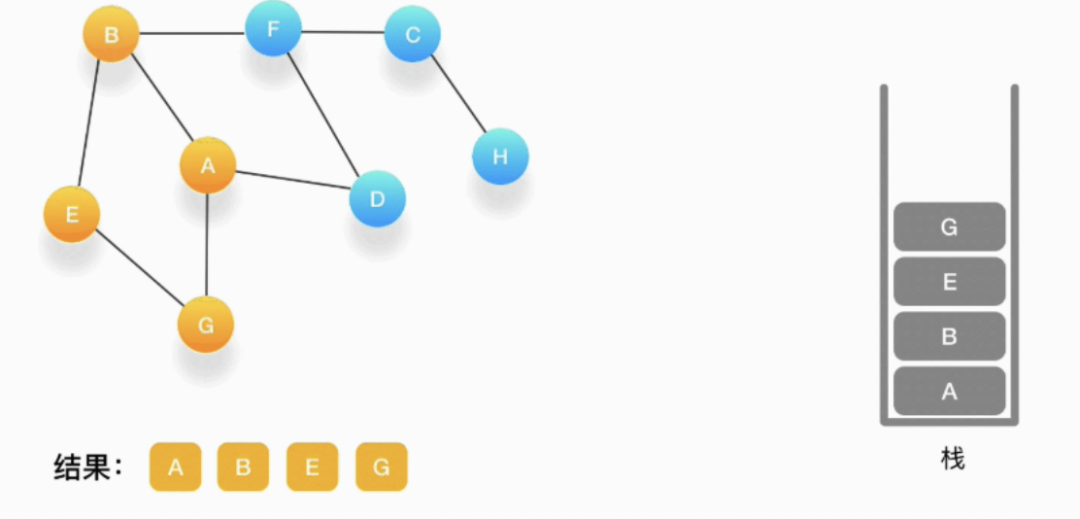
第五步,现在我们在顶点 G 的位置,由于与 G 相连的顶点都被访问过了,类似于我们走到了一个死胡同,必须尝试其他的路口了。所以我们这里要做的就是简单地将 G 从栈里弹出,表示我们从 G 这里已经无法继续走下去了,看看能不能从前一个路口找到出路。
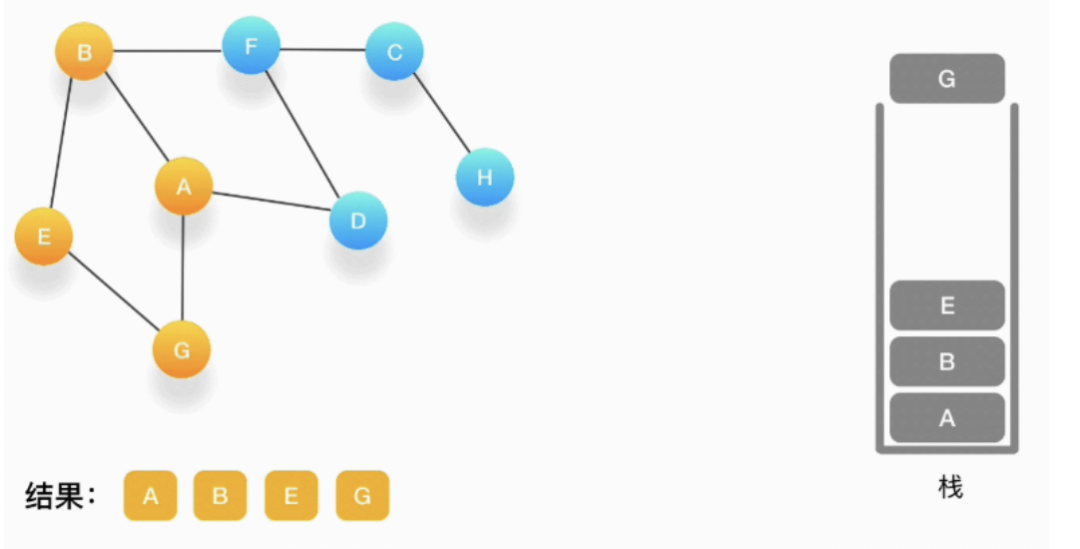
如果发现周围的顶点都被访问了,就把当前的顶点弹出。
第六步,现在栈的顶部记录的是顶点 E,我们来看看与 E 相连的顶点中有没有还没被访问到的,发现它们都被访问了,所以把 E 也弹出去。
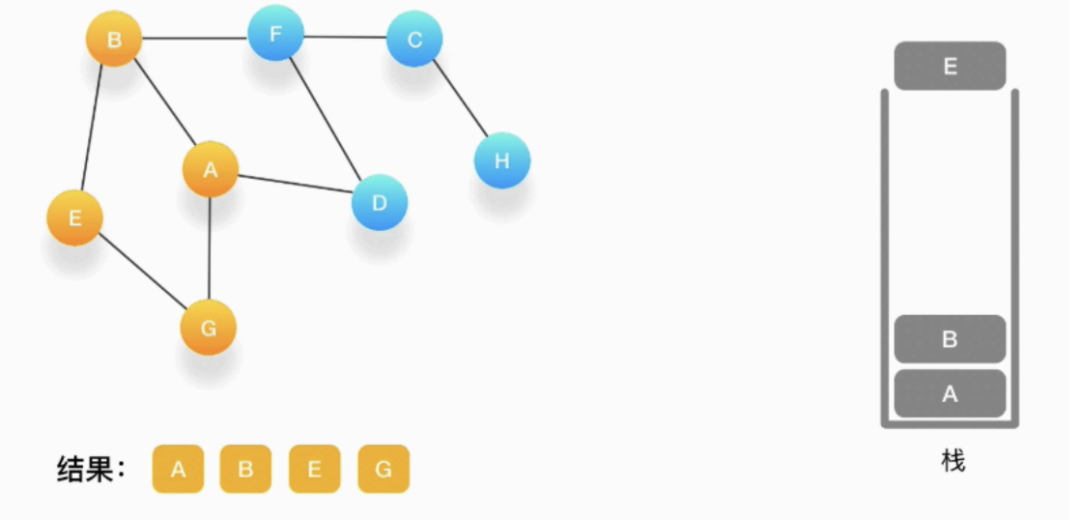
第七步,当前栈的顶点是 B,看看它周围有没有还没被访问的顶点,有,是顶点 F,于是把 F 压入栈, 标记它为访问过,并输出到结果中。
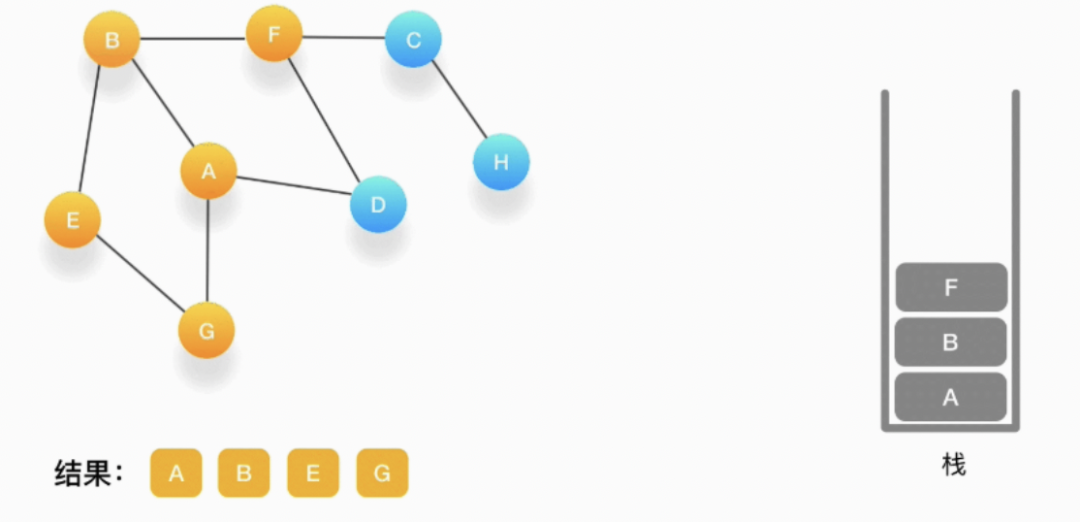
第八步,当前顶点是 F,与 F 相连并且还未被访问到的点是 C 和 D,按照字母顺序来,下一个被访问的点是 C,将 C 压入栈,标记为访问过,输出到结果中。
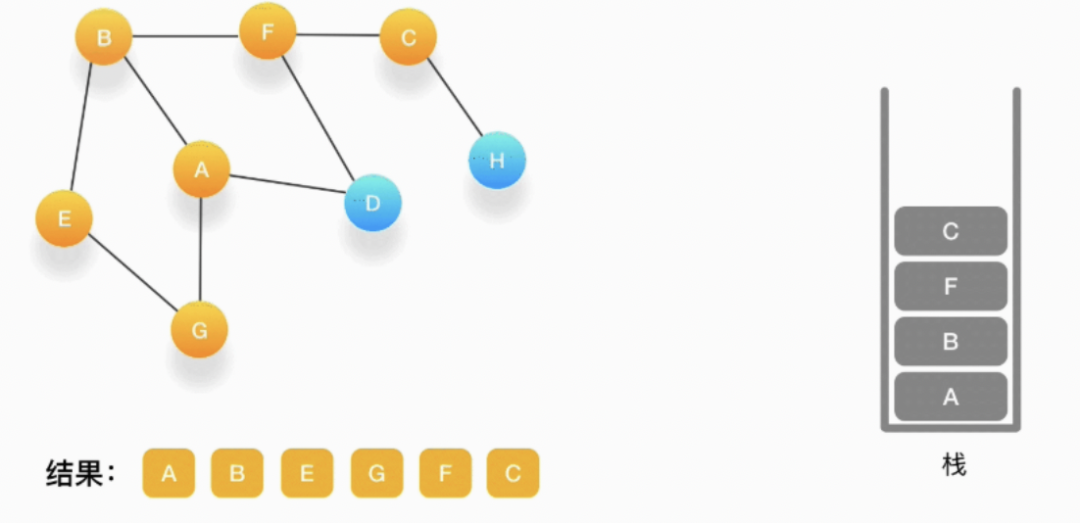
第九步,当前顶点为 C,与 C 相连并尚未被访问到的顶点是 H,将 H 压入栈,标记为访问过,输出到结果中。
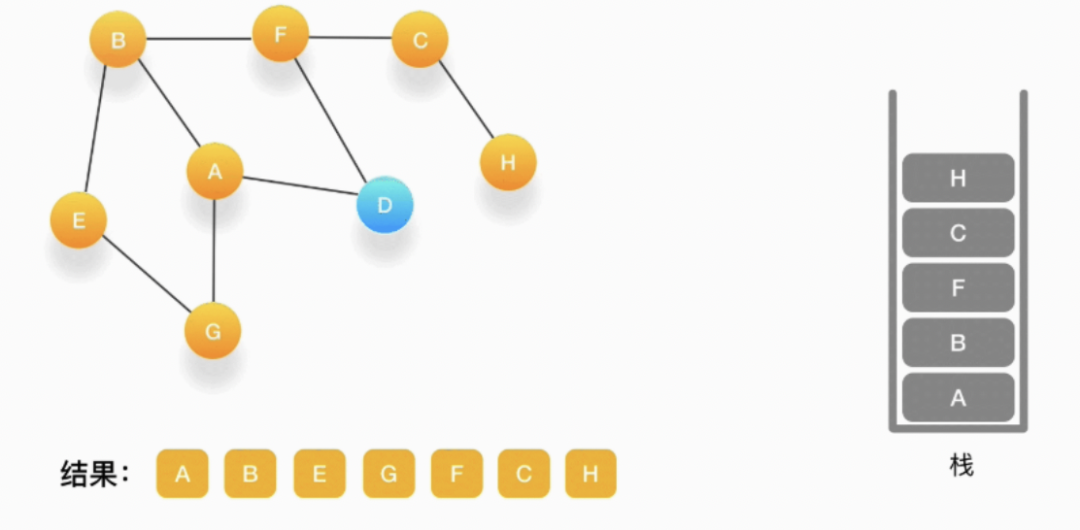
第十步,当前顶点是 H,由于和它相连的点都被访问过了,将它弹出栈。
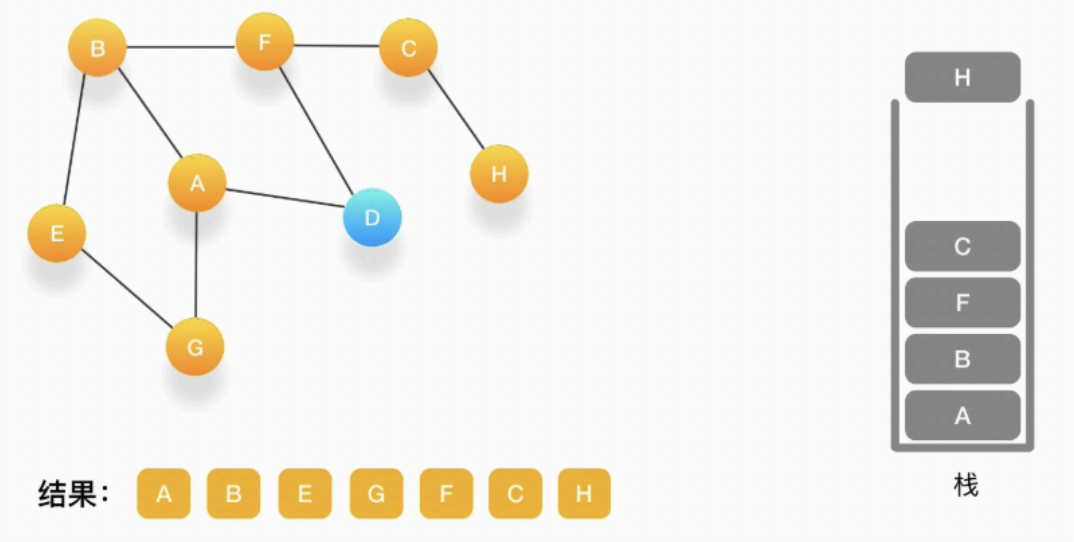
第十一步,当前顶点是 C,与 C 相连的点都被访问过了,将 C 弹出栈。
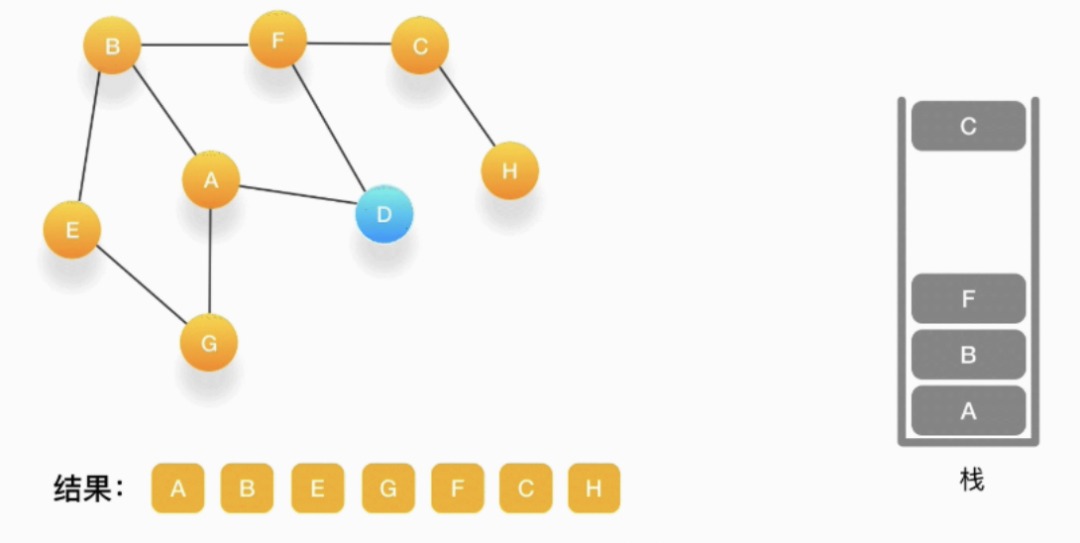
第十二步,当前顶点是 F,与 F 相连的并且尚未访问的点是 D,将 D 压入栈,输出到结果中,并标记为访问过。
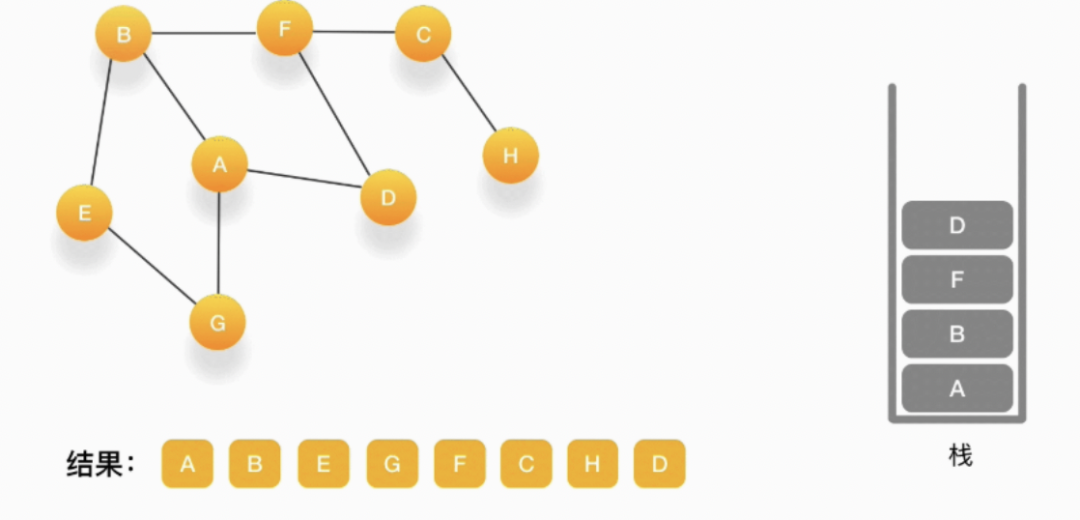
第十三步,当前顶点是 D,与它相连的点都被访问过了,将它弹出栈。以此类推,顶点 F,B,A 的邻居都被访问过了,将它们依次弹出栈就好了。最后,当栈里已经没有顶点需要处理了,我们的整个遍历结束。
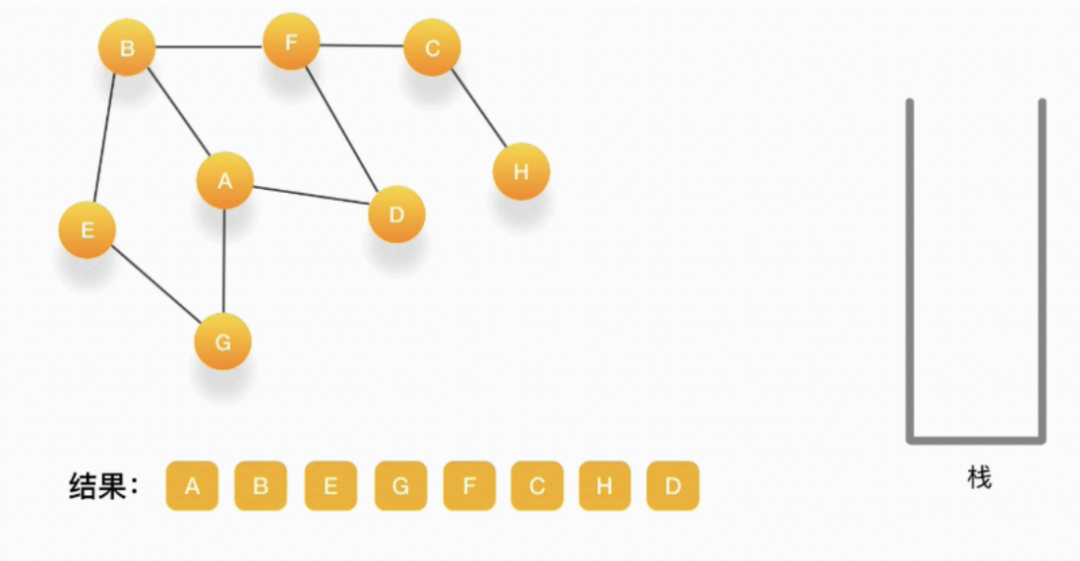
广度优先搜索(BFS,Breadth First Search)
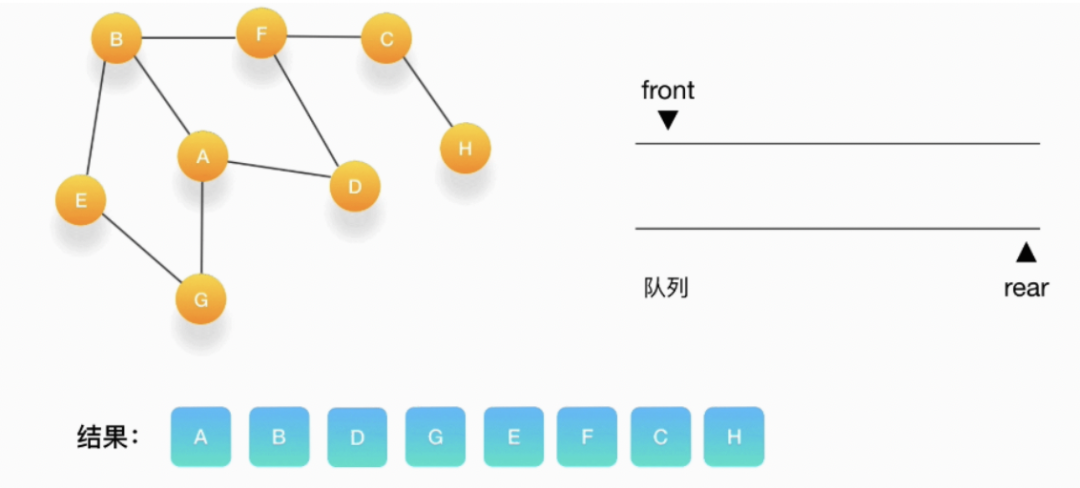
直观地讲,它其实就是一种“地毯式”层层推进的搜索策略,即先查找离起始顶点最近的,然后是次近的,依次往外搜索。假设我们有这么一个图,里面有A、B、C、D、E、F、G、H 8 个顶点,点和点之间的联系如下图所示, 对这个图进行深度优先的遍历。
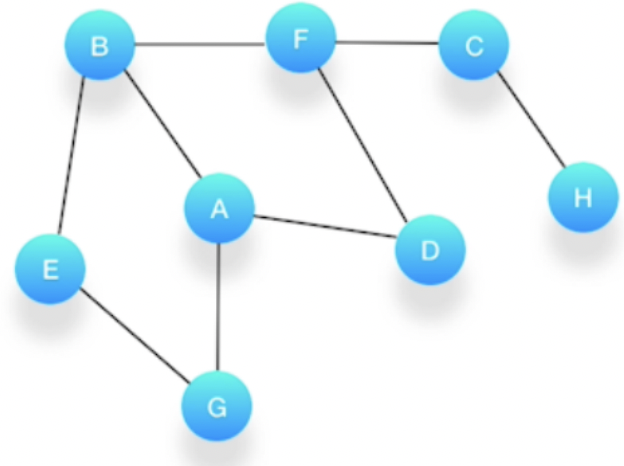
依赖队列(Queue),先进先出(FIFO)。
一层一层地把与某个点相连的点放入队列中,处理节点的时候正好按照它们进入队列的顺序进行。
第一步,选择一个起始顶点,让我们从顶点 A 开始。把 A 压入队列,标记它为访问过。
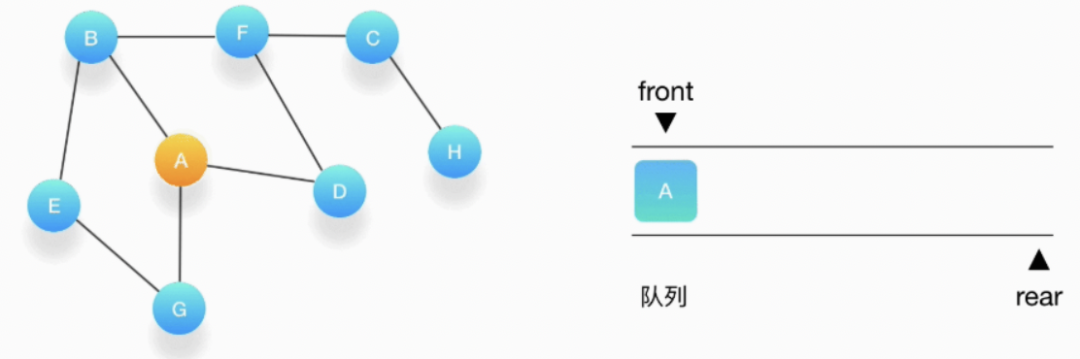
第二步,从队列的头取出顶点 A,打印输出到结果中,同时将与它相连的尚未被访问过的点按照字母大小顺序压入队列,同时把它们都标记为访问过,防止它们被重复地添加到队列中。
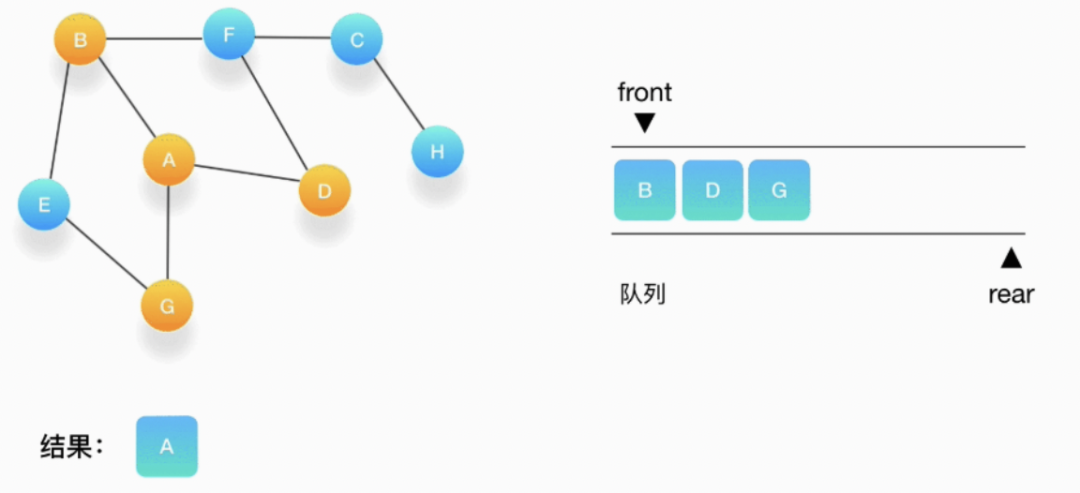
第三步,从队列的头取出顶点 B,打印输出它,同时将与它相连的尚未被访问过的点(也就是 E 和 F) 压入队列,同时把它们都标记为访问过。
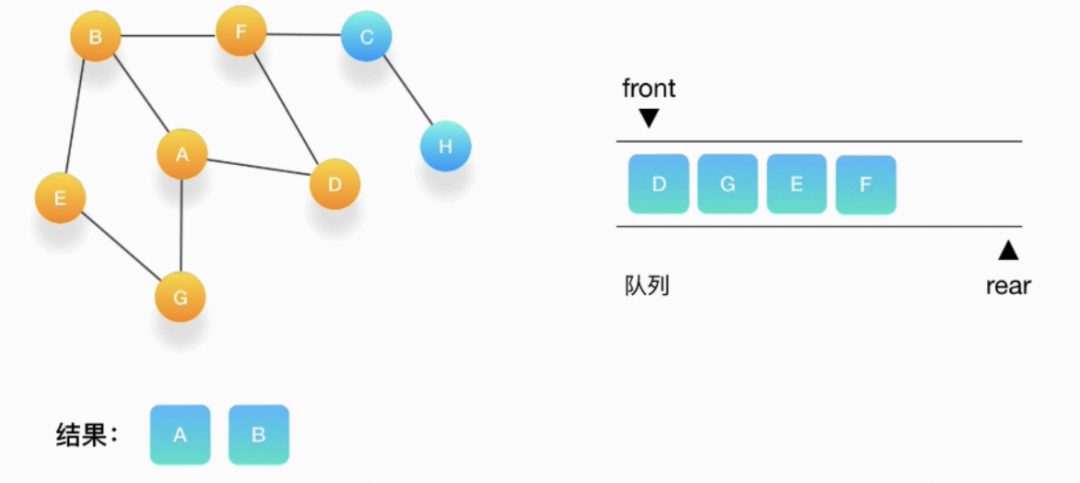
第四步,继续从队列的头取出顶点D,打印输出它,此时我们发现,与 D 相连的顶点 A 和 F 都被标记访问过了,所以就不要把它们压入队列里。
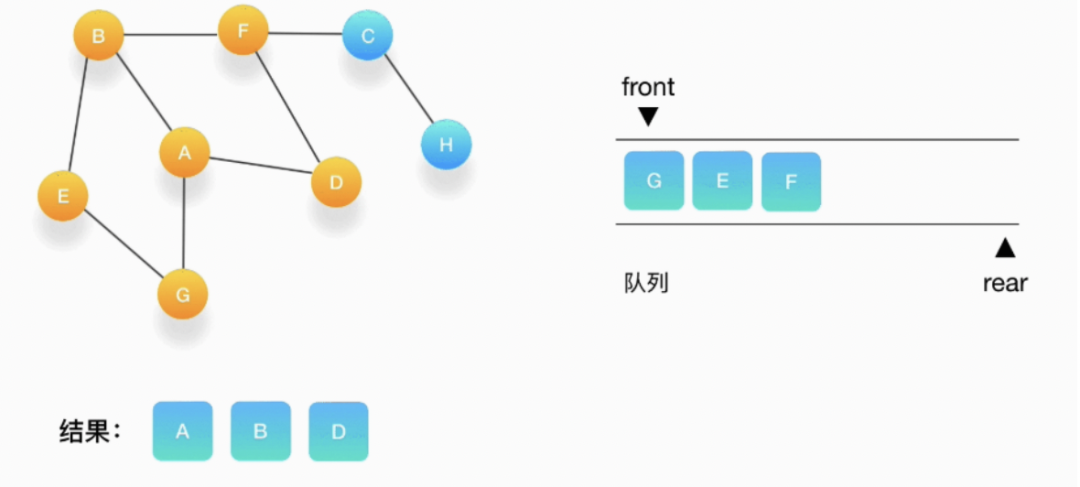
第五步,接下来,队列的头是顶点 G,打印输出它,同样的,G 周围的点都被标记访问过了。我们不做任何处理。
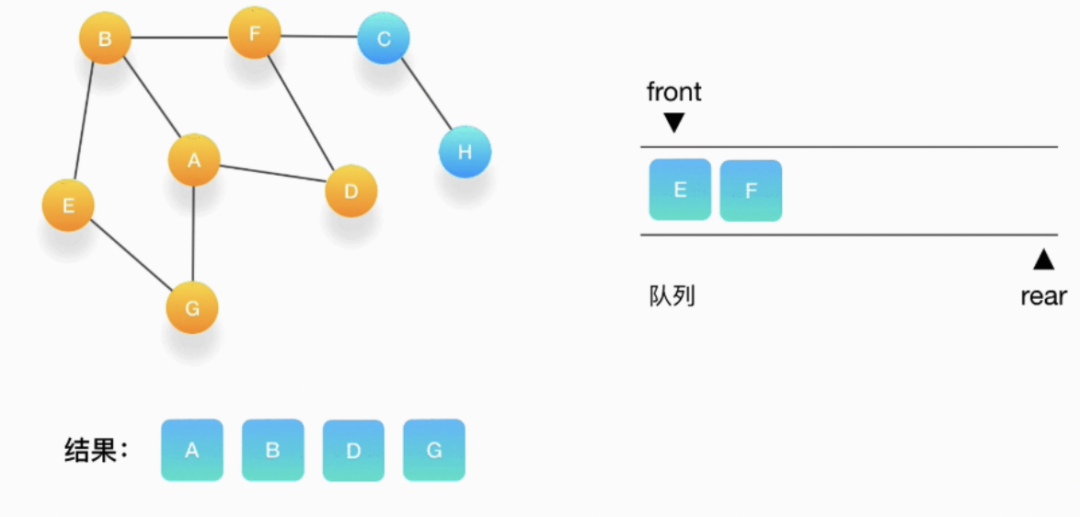
第六步,队列的头是 E,打印输出它,它周围的点也都被标记为访问过了,我们不做任何处理。
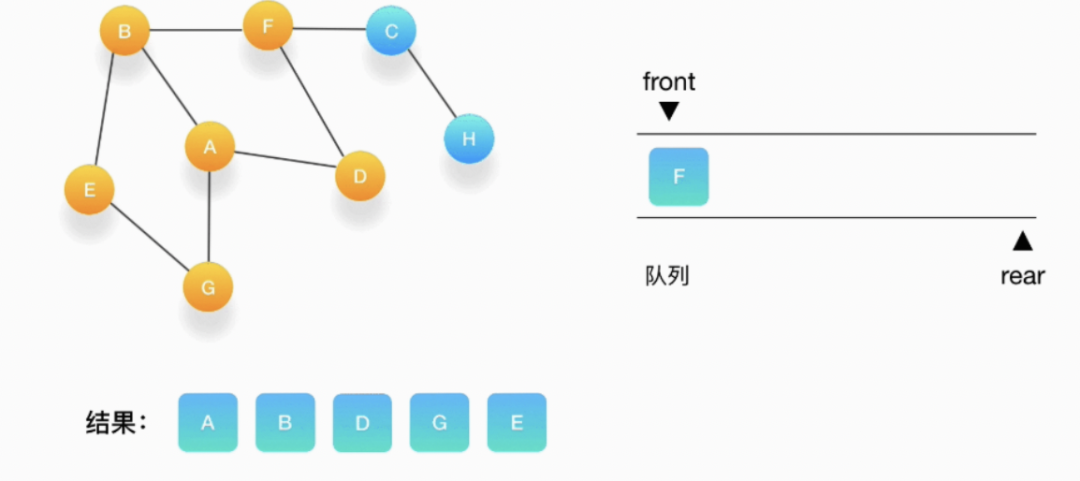
第七步,接下来轮到顶点 F,打印输出它,将 C 压入队列,并标记 C 为访问过。
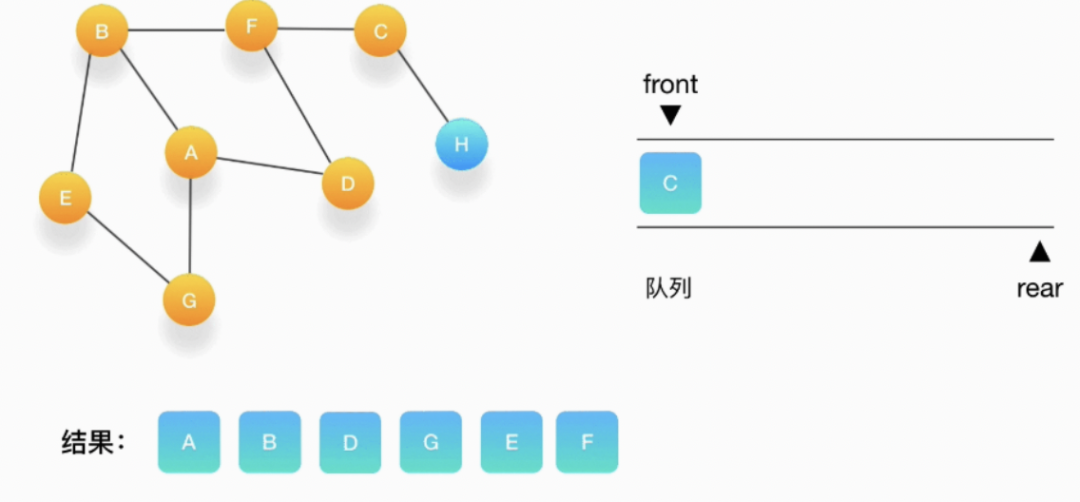
第八步,将 C 从队列中移出,打印输出它,与它相连的 H 还没被访问到,将 H 压入队列,将它标记为访问过。

第九步,队列里只剩下 H 了,将它移出,打印输出它,发现它的邻居都被访问过了,不做任何事情。
社交网络可以用图来表示。这个问题就非常适合用图的广度优先搜索算法来解决,因为广度优先搜索是 层层往外推进的。首先,遍历与起始顶点最近的一层顶点,也就是用户的一度好友,然后再遍历与用户 距离的边数为 2 的顶点,也就是二度好友关系,以及与用户距离的边数为 3 的顶点,也就是三度好友关系。