定义:假设有n 个权值{w1,w2…,Wa},构造一棵有n个叶子结点的二叉树,每个叶子结点带权wk,每个叶子的路径长度为lk,我们谧常记作,则其中带权路径长度WPL最小的二叉树称做赫夫曼树。也有不少书中也称为最优二叉树,我个人觉得为了纪念做出巨大贡献的科学家,既然用他们的名字命名,就应该要坚持用他们的名字称呼,哪怕“最优”更能体现这棵树的品质也应该只作为别名。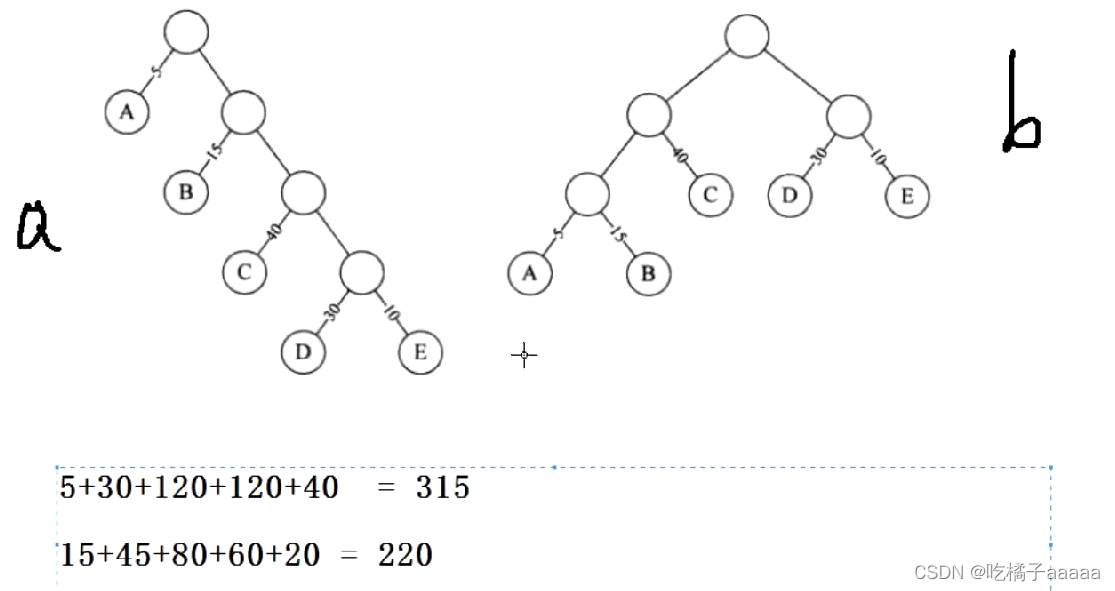
实现代码如下:
#include <iostream>
#include<string.h>
#include<stdio.h>
using namespace std;
struct HaffNode
{
int weight;//权值
int parent;
int lchild;
int rchild;
int flag;//节点是否被用掉
};
void CreateHaff(int* weight, int n, HaffNode* pHaffNode);
void HaffCode(HaffNode* pHaffNode, int n, char code[5][20]);
int main()
{
int weight[] = { 1,15,40,30,10 };
char code[5][20] = { "0" };
int n = sizeof(weight) / sizeof(weight[0]);
HaffNode* pHaffNode = new HaffNode[2 * n - 1];
CreateHaff(weight, n, pHaffNode);
HaffCode(pHaffNode, n, code);
for (int i = 0; i < n; ++i)
puts(code[i]);
return 0;
}
void CreateHaff(int* weight, int n, HaffNode* pHaffNode)
{
int i, j;
int min1, min2;
int min1x, min2x;//最小值的下标
for (int i = 0; i < 2 * n - 1; i++) //初始化数组
{
if (i < n)
{
pHaffNode[i].weight = weight[i];
}
else
{
pHaffNode[i].weight = 0;
pHaffNode[i].parent = 0;
pHaffNode[i].lchild = 0;
pHaffNode[i].rchild = 0;
pHaffNode[i].flag = 0;
}
}
//构造haff
for (i = 0; i < n - 1; ++i)
{
min1 = min2 = 65535;
min1x = min2x = 0;
//循环找min1和min2
for (j = 0; j < n + i; ++j)
{
if (pHaffNode[j].weight < min1 && pHaffNode[j].flag == 0)
{
min2 = min1;//将现有的最小值给次小的
min2x = min1x;
min1 = pHaffNode[j].weight;
min1x = j;
}
else if (pHaffNode[j].weight < min2 && pHaffNode[j].flag == 0)
{
min2 = pHaffNode[j].weight;
min2x = j;
}
}
//用最小的和次小的创建他两的根
pHaffNode[n + i].weight = min1 + min2;
pHaffNode[n + i].lchild = min1x;
pHaffNode[n + i].rchild = min2x;
//重置最小的和次小的父节点下标
pHaffNode[min1x].flag = 1;
pHaffNode[min2x].flag = 1;
pHaffNode[min1x].parent = n + i;
pHaffNode[min2x].parent = n + i;
}
}
void HaffCode(HaffNode* pHaffNode, int n, char code[5][20])
{
int i;
int child;//标志当前节点的下标
int parent;//标志当前节点父节点下标
char str[20] = "0";//存储每个节点的编码
int k = 10;
for (i = 0; i < n; ++i)
{
child = i;
parent = pHaffNode[child].parent;//找到当前child的父节点下标
k = 10;
while (parent != 0)
{
//看当前节点child是parent的左孩子还是右孩子
if (child == pHaffNode[parent].lchild)
str[k--] = '0';
else if (child == pHaffNode[parent].rchild)
str[k--] = '1';
//继续向上追溯,直到根节点
child = parent;
parent = pHaffNode[child].parent;
}
//将当前str中存储的当前节点的编码拷贝到code中
strcpy_s(code[i], str + k + 1);
}
}
运行结果: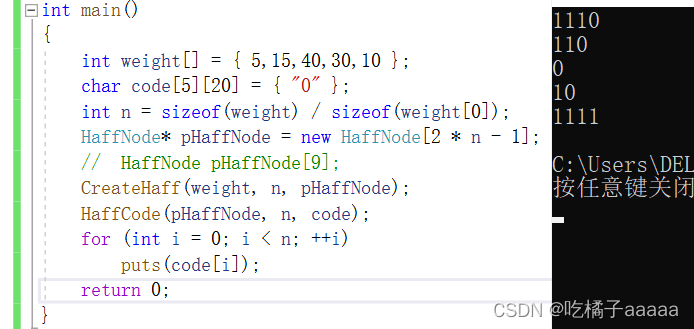
版权声明:本文为weixin_58368590原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。