平衡树以及JAVA实现

一.平衡二叉树（Balanced Binary Tree）又被称为AVL树（有别于AVL算法）。

        它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。这个方案很好的解决了二叉查找树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对二叉查找树来说，时间上稳定了很多。

二.失衡类型、旋转平衡技巧和代码实现

LL类型：在失衡结点的左孩子的左子树上插入- - -LL右旋

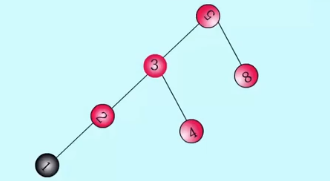
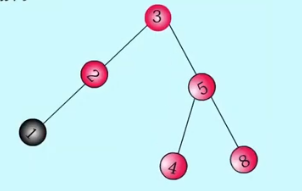
代码实现：

 // LL平衡旋转(右单旋转)
    public static AVLNode LLRotate(AVLNode p){ // p为失衡点
        AVLNode lsubtree = p.lchild;
        p.lchild = lsubtree.rchild; // 将失衡点p的左孩子lsubtree的右子树成为失衡点p的左子树
        lsubtree.rchild = p; // 将失衡点作为lsubtree的右子树
        // 重新调整失衡点及其左孩子节点的高度值(只有这两个节点的高度值可能发生改变)
        p.height = Math.max(getHeight(p.lchild), getHeight(p.rchild)) + 1;
        lsubtree.height = Math.max(getHeight(lsubtree.lchild), p.height) + 1;
        return lsubtree; // 失衡点p的左孩子成为新的根节点(取代原失衡点的位置)
    }

LR类型：在失衡结点的右孩子的左子树上插入- - -LR右旋

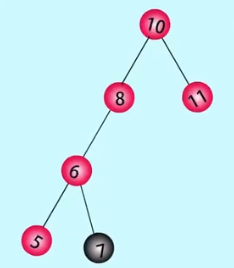
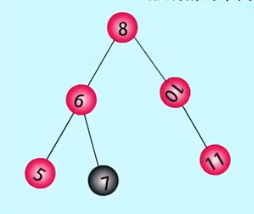
// LR平衡旋转(先左后右双旋转)
    public static AVLNode LRRotate(AVLNode p){
        p.lchild = RRRotate(p.lchild); // 先将失衡点p的左子树进行RR平衡旋转
        return LLRotate(p); // 再将失衡点p进行LL平衡旋转并返回新节点代替原失衡点p

    }

RL类型：在失衡结点的左孩子的右子树上插入 - - -RL旋转

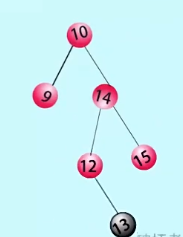
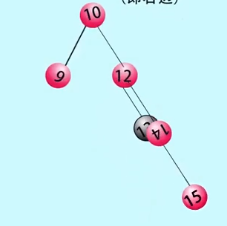
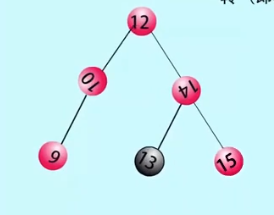
// RL平衡旋转(先右后左双旋转)
    public static AVLNode RLRotate(AVLNode p){
        p.rchild = LLRotate(p.rchild); // 先将失衡点p的右子树进行LL平衡旋转 
        return RRRotate(p); // 再将失衡点p进行RR平衡旋转并返回新节点代替原失衡点p
    }

RR类型：在失衡结点的右孩子的右子树上插入- - -RR右旋

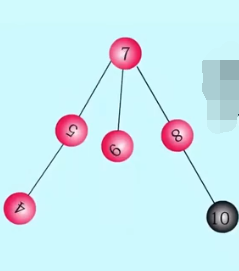
// RR平衡旋转(左单旋转)
    public static AVLNode RRRotate(AVLNode p){
        AVLNode rsubtree = p.rchild;
        p.rchild = rsubtree.lchild; // 将失衡点p的右孩子rsubtree的左子树成为失衡点p的右子树
        rsubtree.lchild = p; // 将失衡点p作为rsubtree左子树
        // 重新调整失衡点及其右孩子节点的高度值
        p.height = Math.max(getHeight(p.lchild), getHeight(p.rchild)) + 1;
        rsubtree.height = Math.max(getHeight(rsubtree.lchild), getHeight(rsubtree.rchild)) + 1;
        return rsubtree; //  失衡点p的右孩子成为新的根节点(取代原失衡点的位置)
    }

三、平衡二叉树的定义以及插入删除

平衡二叉树的插入删除和二叉树的几乎一样，但操作完之后需要判断一下高度差是否失衡，如果失衡要进行旋转调整。

下面是完整代码：

package Demo05;

public class Demo05{
public static void main(String[] args) {
        AVLNode root = null;
        int []a= {20,8,2,4,5,6,28,18,19,33,25,26};
        for(int i = 0; i <10; i++){
            root = insert(root, a[i]);
        }
        insert(root, 3);
        inOrder(root);
        System.out.println();
//      System.out.println("height: " + (root.height + 1) + " " + (int)Math.ceil(Math.log(10)/ Math.log(2))); // 树的高度为叶子节点的最大深度加上1(根节点为第一层)
        remove(root, 18);
        inOrder(root);
    }

    public static AVLNode insert(AVLNode root, int data) {
        if (root == null) {
            root = new AVLNode(data);
            return root;
        }
        if (data <= root.data) { // 插入到其左子树上
            root.lchild = insert(root.lchild, data);
            if (getHeight(root.lchild) - getHeight(root.rchild) > 1) { // 由于是向当前root树的左边插入，所以左子树高度必定不小于右子树高度(条件>1实质上等价于==2)
                if (data <= root.lchild.data) { // 最后插入的叶子结点在该root树的左孩子的左边
                    root = LLRotate(root); // 将调整后的root返回给其父节点的左子树域
                }else{ // 最后插入的叶子结点在该root树的左孩子的右边
                    root = LRRotate(root);
                }
            }
        }else{ // 插入到其右子树上
            root.rchild = insert(root.rchild, data);
            if(getHeight(root.rchild) - getHeight(root.lchild) > 1){
                if(data <= root.rchild.data){
                    root = RLRotate(root);
                }else{
                    root = RRRotate(root);
                }
            }
        }
        // 当插入新的节点后，从这个节点到根节点的最短路径上的节点的高度值一定会发生改变，另外当出现失衡点时，这个失衡点的所有祖先节点的高度值也可能会发生改变
        root.height = Math.max(getHeight(root.lchild), getHeight(root.rchild)) + 1; // 重新调整root节点的高度值
        return root;
    }

    public static AVLNode remove(AVLNode root, int data){
        if(root == null){ // 没有找到删除的节点
            return null;
        }
        if(data < root.data){ // 在左子树上删除
            root.lchild = remove(root.lchild, data);
            if(getHeight(root.rchild) - getHeight(root.lchild) > 1){ // 在左子树上删除，右子树高度一定不小于左子树高度
                if(getHeight(root.rchild.lchild) > getHeight(root.rchild.rchild)){
                    root = RLRotate(root);
                }else{
                    root = RRRotate(root);
                }
            }
        }else if(data == root.data){ // 找到删除的节点
            if(root.lchild != null && root.rchild != null){ // 删除的节点既有左子树又有右子树
                root.data = findNextNode(root).data; // 将失衡点的data域更改为其直接后继节点的data域
                root.rchild = remove(root.rchild, root.data); // 将问题转换为删除其直接后继节点
            }else{ // 只有左子树或者只有右子树或者为叶子结点的情况
                root = (root.lchild == null) ? root.rchild : root.lchild;
            }
        }else{ // 在root的右子树上查找删除节点
            root.rchild = remove(root.rchild, data);
            if(getHeight(root.lchild) - getHeight(root.rchild) > 1){
                if(getHeight(root.lchild.lchild) > getHeight(root.lchild.rchild)){
                    root = LLRotate(root);
                }else{
                    root = LRRotate(root);
                }
            }
        }
        if(root != null){ // 更新root的高度值
            root.height = Math.max(getHeight(root.lchild), getHeight(root.rchild)) + 1;
        }
        return root;
    }

    // LL平衡旋转(右单旋转)
    public static AVLNode LLRotate(AVLNode p){ // p为失衡点
        AVLNode lsubtree = p.lchild;
        p.lchild = lsubtree.rchild; // 将失衡点p的左孩子lsubtree的右子树成为失衡点p的左子树
        lsubtree.rchild = p; // 将失衡点作为lsubtree的右子树
        // 重新调整失衡点及其左孩子节点的高度值(只有这两个节点的高度值可能发生改变)
        p.height = Math.max(getHeight(p.lchild), getHeight(p.rchild)) + 1;
        lsubtree.height = Math.max(getHeight(lsubtree.lchild), p.height) + 1;
        return lsubtree; // 失衡点p的左孩子成为新的根节点(取代原失衡点的位置)
    }

    // RR平衡旋转(左单旋转)
    public static AVLNode RRRotate(AVLNode p){
        AVLNode rsubtree = p.rchild;
        p.rchild = rsubtree.lchild; // 将失衡点p的右孩子rsubtree的左子树成为失衡点p的右子树
        rsubtree.lchild = p; // 将失衡点p作为rsubtree左子树
        // 重新调整失衡点及其右孩子节点的高度值
        p.height = Math.max(getHeight(p.lchild), getHeight(p.rchild)) + 1;
        rsubtree.height = Math.max(getHeight(rsubtree.lchild), getHeight(rsubtree.rchild)) + 1;
        return rsubtree; //  失衡点p的右孩子成为新的根节点(取代原失衡点的位置)
    }

    // LR平衡旋转(先左后右双旋转)
    public static AVLNode LRRotate(AVLNode p){
        p.lchild = RRRotate(p.lchild); // 先将失衡点p的左子树进行RR平衡旋转
        return LLRotate(p); // 再将失衡点p进行LL平衡旋转并返回新节点代替原失衡点p

    }

    // RL平衡旋转(先右后左双旋转)
    public static AVLNode RLRotate(AVLNode p){
        p.rchild = LLRotate(p.rchild); // 先将失衡点p的右子树进行LL平衡旋转 
        return RRRotate(p); // 再将失衡点p进行RR平衡旋转并返回新节点代替原失衡点p
    }

    private static class AVLNode{
        private AVLNode lchild = null;
        private AVLNode rchild = null;
        private int data;
        private int height; // 记录该节点所在的高度

        public AVLNode(int data){
            this.data = data;
        }
    }

    public static int getHeight(AVLNode p){
        return p == null ? -1 : p.height; // 空树的高度为-1
    }

    public static void inOrder(AVLNode root){
        if(root != null){
            inOrder(root.lchild);
            System.out.print(root.data + " ");
            inOrder(root.rchild);
        }
    }

    // 得到p节点的后继节点(中序遍历),实际上也是p节点的右子树上的关键字值最小的节点
    public static AVLNode findNextNode(AVLNode p){
        if(p == null){
            return null;
        }
        AVLNode r = p.rchild;
        while(r != null && r.lchild != null){
            r = r.lchild;
        }
        return r;
    }

    // 得到p节点的直接前驱节点(中序遍历),实际上也是p节点的左子树上的关键字值最大的节点
    public static AVLNode findPreviousNode(AVLNode p){
        if(p == null){
            return null;
        }
        AVLNode l = p.lchild;
        while(l != null && l.rchild != null){
            l = l.rchild;
        }
        return l;
    }
}