前缀和问题

一：什么是前缀和

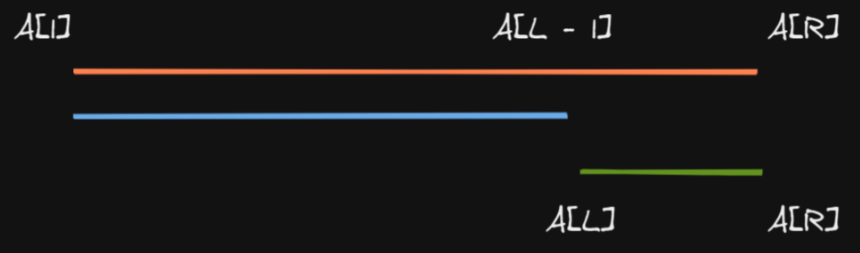
       前缀和可以简单理解为「数列的前 n项的和」，是一种重要的预处理方式，能大大降低查询的时间复杂度

 说白了有点类似高中的数列，而且前缀和之差可以求出一些连续数组元素的值

 一般用于解决一些连续数组的问题

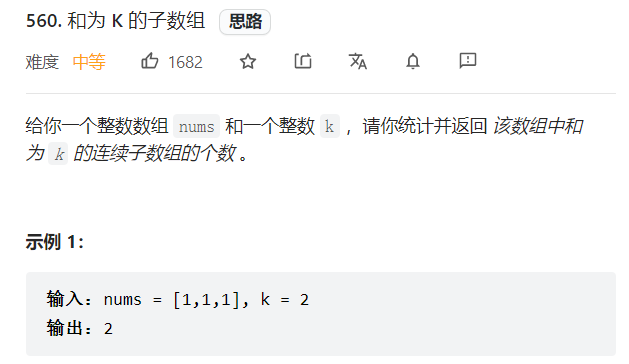
二：前缀和应用----和为k的子数组

题目：

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
    //创建前缀和
    int* prefix=new int[nums.size()+1];
    prefix[0]=0;
    for(int i=0;i<nums.size();i++){
        prefix[i+1]=nums[i]+prefix[i];
    }
    //声明哈希表
    unordered_map<int,int> mp;//K---prefix[i],V---次数
    mp[0]=1;//prefix[0]=0;
    //判断过程
    int res=0;
    for(int i=0;i<nums.size();i++){
        //当前前缀和减去给出k值是否在哈希表中存在
        if(mp.find(prefix[i+1]-k)!=mp.end())//找到了
            res+=mp[prefix[i+1]-k];//频次累计
        //更新哈希表
        mp[prefix[i+1]]++;
    }
    return res;
    }
};

 这里注意：从prefix[1]去判断.这里前缀和数组是累加的，而且向前找，直接定义一个累加变量pre即可。

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
    //创建前缀和
    int* prefix=new int[nums.size()+1];
    int pre=0;
    //声明哈希表
    unordered_map<int,int> mp;//K---prefix[i],V---次数
    mp[0]=1;//prefix[0]=0;
    //判断过程
    int res=0;
    for(int i=0;i<nums.size();i++){
        //当前前缀和减去给出k值是否在哈希表中存在
        pre+=nums[i];
        if(mp.find(pre-k)!=mp.end())//找到了
            res+=mp[pre-k];//频次累计
        //更新哈希表
        mp[pre]++;
    }
    return res;
    }
};

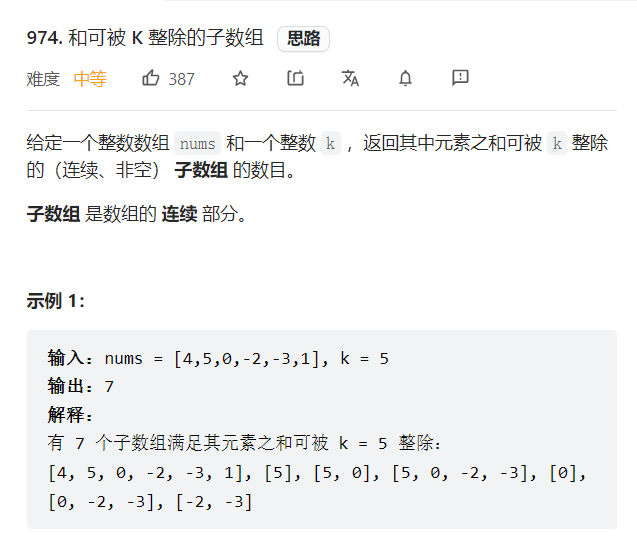
二：求mod相同

题目：

题目涉及了同余数的知识：(a-b)modk==0等价于amod k==b mod k

class Solution {
public:
    int subarraysDivByK(vector<int>& nums, int k) {
        int pre=0;//累计求前缀和变量
        unordered_map<int,int> mp;//哈希表，存所有前缀和结果
        mp[0]=1;//第一个元素nums[0]:视为pre[1]-pre[0]
        int res=0;
        for(int i=0;i<nums.size();i++){
            pre+=nums[i];
            //同余数：pre[i]mod k==pre[j]mod k
            int m=((pre%k)+k)%k;//+k是避免负数
            if(mp.find(m)!=mp.end()){
                res+=mp[m];
            }
            mp[m]++;
        }
        return res;
    }
};

 这里的哈希表存储的余数--注意哈希表内容的k,v要因题而异

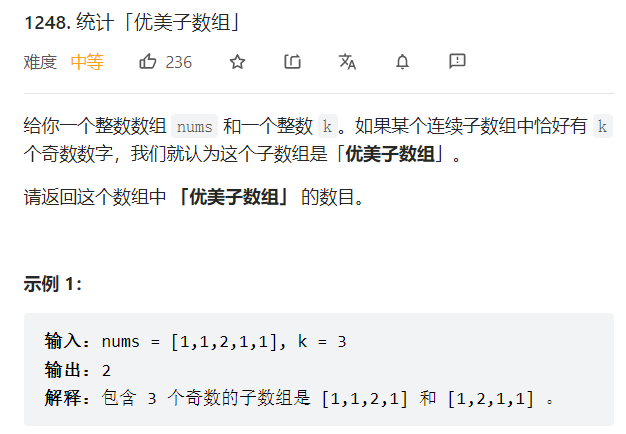
 三：求奇数间隔次数

class Solution {
public:
    int numberOfSubarrays(vector<int>& nums, int k) {
       int odd=0;//计算当前前缀和的奇数个数
       unordered_map<int,int> mp;//key:奇数个数，次数
       mp[0]=1;
       int res=0;
       for(int i=0;i<nums.size();i++){
           odd+=(nums[i]%2==1)?1:0;
           if(mp.find(odd-k)!=mp.end()){
               res+=mp[odd-k];
           }
           mp[odd]++;
       }
       return res;
    }
};

这里：前缀记录奇数的个数，查找表记录出现过的奇数的个数

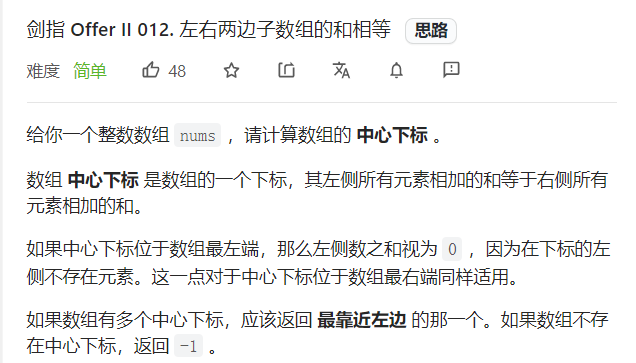
四：左一半==右一半 

题目：

class Solution {
public:
    int pivotIndex(vector<int>& nums) {
        //遍历一遍元素，求出数组总和
        int presum=0;
        for(int i=0;i<nums.size();i++){
          presum+=nums[i];
        }
        //再遍历一遍数组，求满足题意的
        int leftsum=0;//下标左元素之和
        for(int i=0;i<nums.size();i++){
            if(leftsum==presum-nums[i]-leftsum){//右一半=全-左一半-该元素
                return i;
            }
            leftsum+=nums[i];
        }
        return -1;
    }
};