LeetCode312. 戳气球

解题思路

官方题解
参考题解

核心思想:
由于戳气球的操作会导致两个气球从不相邻变成相邻，使得后续操作难以处理。于是我们倒过来看这些操作，将全过程看成每次添加一个气球。
solve(i, j)表示 开区间(i, j) 所能获得的最大硬币数。当开区间只包含一个气球mid时，solve(i, j) = val[i] * val[mid] * val[j]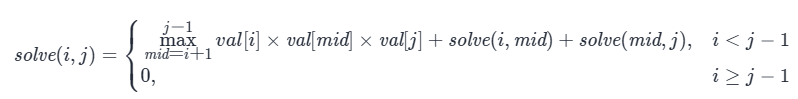

记忆化搜索

自顶向下分治+递归+记忆

/*
解法一: 记忆化搜索
	由于戳气球的操作会导致两个气球从不相邻变成相邻，使得后续操作难以处理。
	于是我们倒过来看这些操作，将全过程看成每次添加一个气球。
*/
func maxCoins(nums []int) int {
	n := len(nums)

	/*
		初始化val切片，左右边界都视为值为1的气球
	*/
	val := make([]int, n+2)
	val[0], val[n+1] = 1, 1
	for i := 1; i < n+1; i++ {
		val[i] = nums[i-1]
	}

	/*
		初始化结果数组，res[i][j]表示开区间(i, j)
		所能获取的最大硬币数
	*/
	res := make([][]int, n+2)
	for i := range res {
		res[i] = make([]int, n+2)
		for j := range res[i] {
			res[i][j] = -1
		}
	}

	return solve(0, n+1, val, res)
}

/*
分治算法+记忆化搜索
*/
func solve(left, right int, val []int, res [][]int) int {
	if left >= right-1 {
		return 0
	}

	// 已经搜索过了，直接返回结果
	if res[left][right] != -1 {
		return res[left][right]
	}

	for mid := left + 1; mid < right; mid++ {
		sum := val[left] * val[mid] * val[right]
		// 递归计算左区间和右区间的硬币数量
		sum += solve(left, mid, val, res) + solve(mid, right, val, res)
		res[left][right] = max(res[left][right], sum)
	}

	return res[left][right]
}

/**
返回两个整数中的较大值
 */
func max(i, j int) int {
	if i >= j {
		return i
	}
	return j
}

动态规划

自底向上

/*
解法二: 动态规划
	既然有了记忆化搜索，只需要将自顶向下的搜索改为自底向上的搜索，
	那就是动态规划了

	状态变量dp[i][j]，表示开区间(i, j)所能获得最大硬币数
	dp[i][j] = max(dp[i][k] + dp[k][j] + val[i] * val[k] * val[j]), i < k < j
*/
func maxCoins(nums []int) int {
	n := len(nums)

	/*
		初始化val切片，左右边界都视为值为1的气球
	*/
	val := make([]int, n+2)
	val[0], val[n+1] = 1, 1
	for i := 1; i < n+1; i++ {
		val[i] = nums[i-1]
	}
	
	dp := make([][]int, n+2)
	for i := range dp {
		dp[i] = make([]int, n+2)
	}
	for i := n - 1; i >= 0; i-- {
		for j := i + 2; j <= n+1; j++ {
			for k := i + 1; k < j; k++ {
				sum := val[i] * val[k] * val[j]
				sum += dp[i][k] + dp[k][j]
				dp[i][j] = max(dp[i][j], sum)
			}
		}
	}

	return dp[0][n+1]
}

/**
返回两个整数中的较大值
 */
func max(i, j int) int {
	if i >= j {
		return i
	}
	return j
}