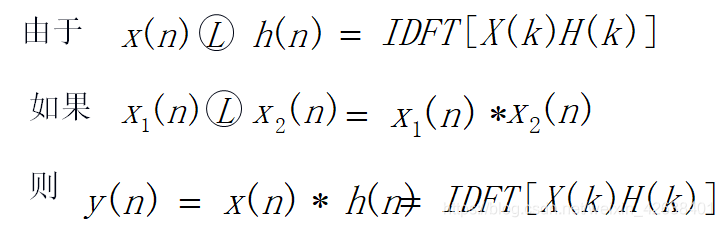
离散傅里叶变换（DFT）

             ——有限长序列的离散频域表示

一、预备知识

1.余数运算表达式

设有限长序列x(n)的长度为N，（0~N-1期间非0），将其以N为周期作周期延拓，所得的周期信号记为

四.从DFS到DFT：

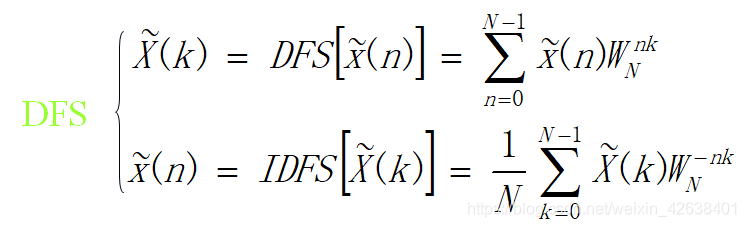
从上式可知，DFS,IDFS的求和只限定在n=0到n=N-1,及k=0到N-1的主值区间进行。

因此可得到新的定义，即有限长序列的离散傅氏变换(DFT)的定义：

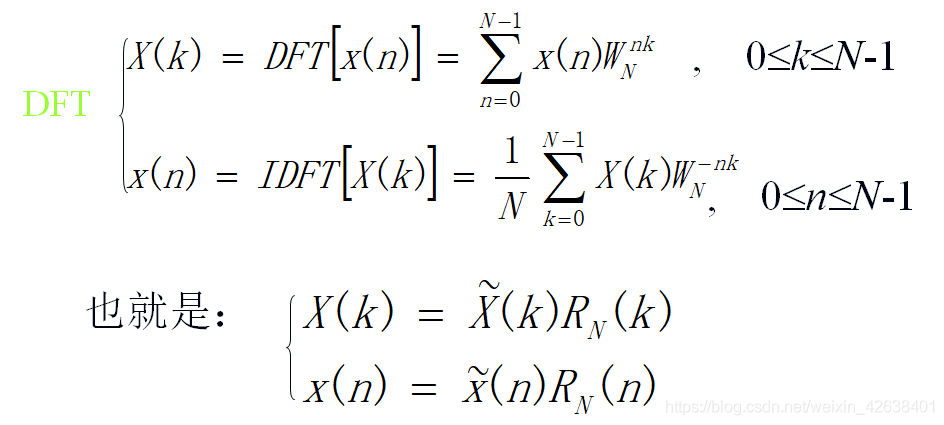
x(n)与X(k)是有限长序列的离散傅里叶变换对。

DFT与序列的DTFT和z变换的关系： 

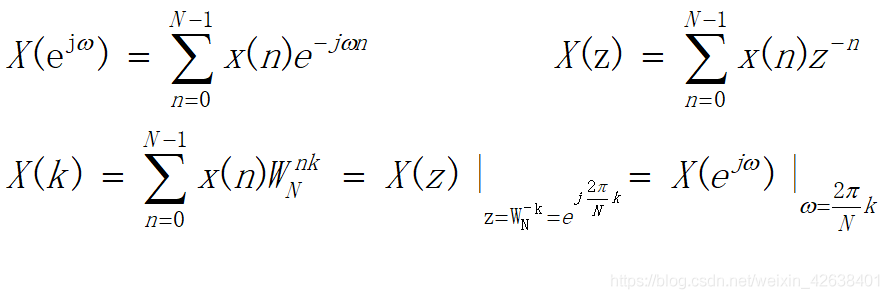
x(n)的N点DFT是:

x(n)的z变换在单位圆上的N点等间隔抽样；

  x(n)的DTFT在区间[0, 2Π]上的N点等间隔抽样。  

DFT的性质

1.线性

1）两序列都是N点时

2）长度N1,N2不等时

注：当两个序列作不同N点DFT时，对应的频域值

        是z平面上不同点上的值，不能在频域相加。

2.序列的圆周移位

1）定义：一个有限长序列 x(n)的圆周移位定义为

 这里包括三层意思：

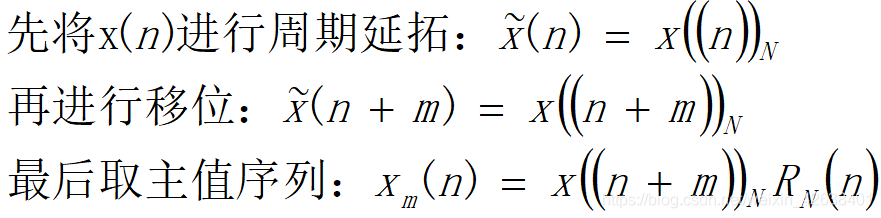
2）圆周移位的含义

∵    取主值序列，即只观察n=0到N-1这一主值区间，

   ∴     当某一抽样从此区间一端移出时，与它相同值的抽样又从此区间的另一端进来。

        如果把 x(n)排列一个 N等分的圆周 上，序列的移位就相当于x(n)在圆上旋转，故称作圆周移位。

3）圆周移位的性质

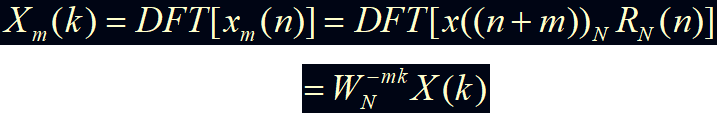
说明：有限长序列的圆周移位导致频谱线性相移，而对频谱幅度无影响。

4）调制特性

说明：时域序列的调制等效于频域的圆周移位 

推广：

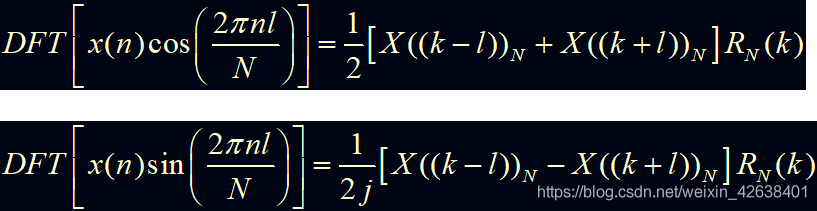
3.共轭对称性

1）周期序列共轭对称分量与共轭反对称分量

      周期为N的周期序列的共轭对称分量：

2）有限长序列的圆周共轭对称分量与圆周共轭反对称分量

圆周共轭对称序列满足：

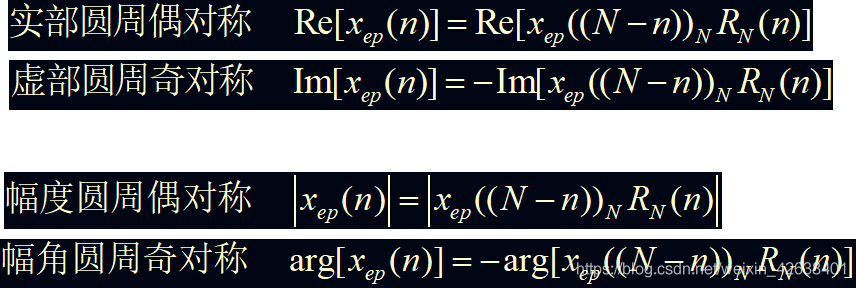
圆周共轭反对称序列满足：

长度为N的有限长序列可分解圆周共轭对称分量与圆周共轭反对称 分量，二者的长度也为N：

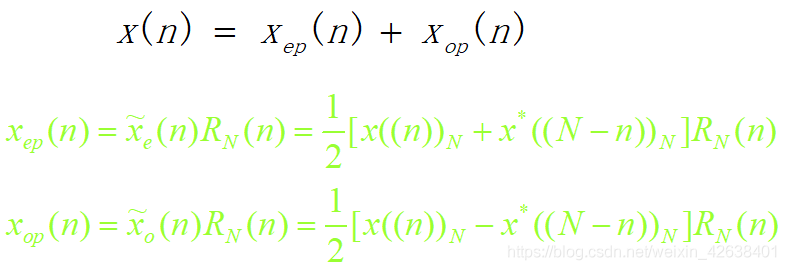
这是因为

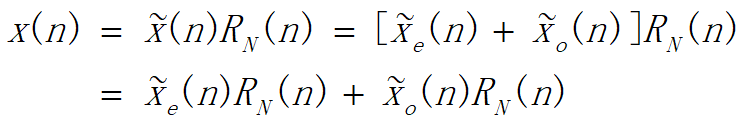
3） 共轭对称特性之一 

4）共轭对称特性之二

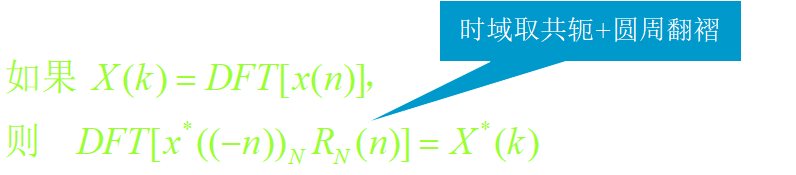
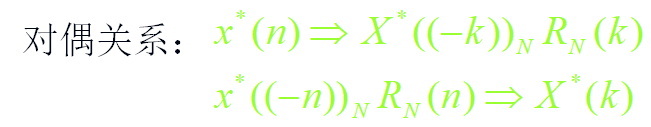
5）共轭对称特性之三

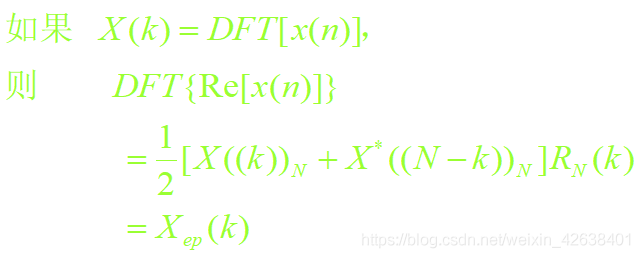
频域圆周共轭对称

（幅度圆周偶对称，  相角圆周奇对称）

6）共轭对称特性之四

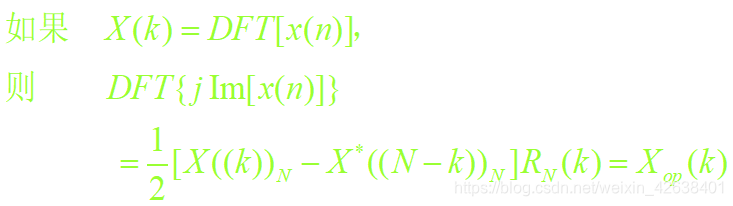
7）共轭对称特性之五、六

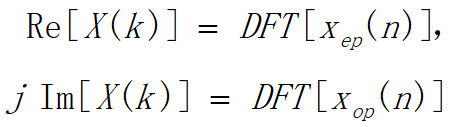
9）实、虚序列的对称特性

•当x(n)为实序列时，根据特性之三，则   X(k)=Xep(k)  

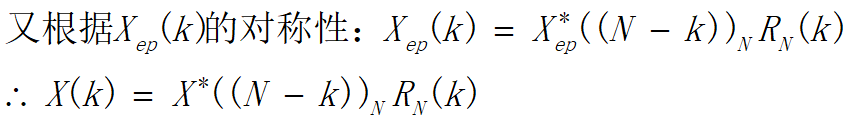
•当x(n)为纯虚序列时，根据特性之四，则 X(k)=Xop(k) 

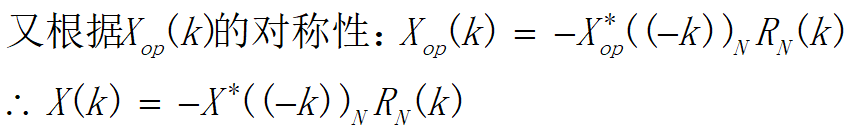
4.DFT形式下的parseval定理

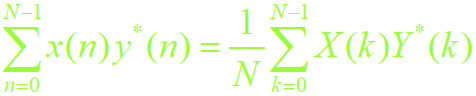
说明：时域计算的能量与在频域计算的能量是相等的。 

5.圆周卷积定理

1）圆周卷积和的定义

两个长度为N的序列 的如下计算称为圆周卷积和，用符号 表示：（N表示圆周卷积的点数）

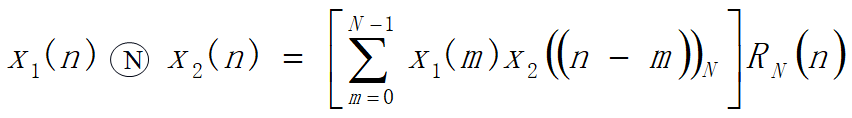
性质：

说明：相对于圆周卷积，前面介绍的卷积称为线性卷积。 

2）时域圆周卷积定理

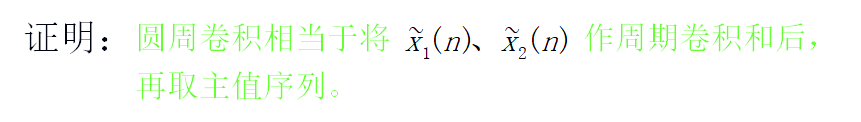
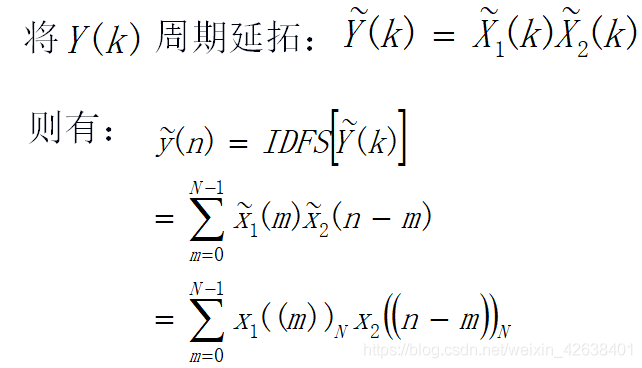
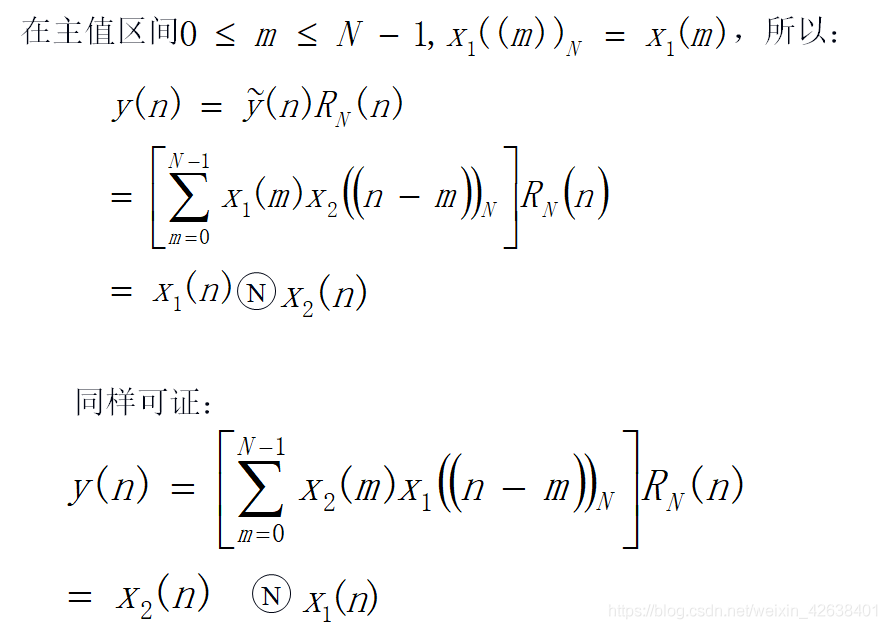
3）频域圆周卷积定理

4）圆周卷积计算步骤

圆周翻褶、圆周移位、相乘、相加

注：两个序列应有相同的长度N，才能进行N点圆周卷积；

        如果长度不等，应将短序列补0，以使长度相等。

6.线性相关与圆周相关

1）线性相关

相关：两个信号之间的关联性。

    线性相关定义为

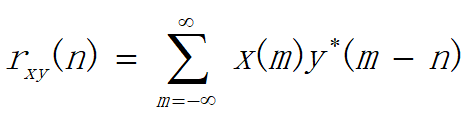
注意与线性卷积的差异：

      线性卷积：

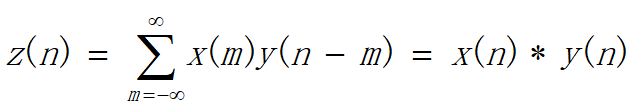
卷积有翻褶，相关没有翻褶；相关有取共轭。

2)圆周相关

定义为：

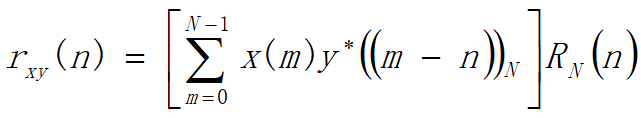
性质：

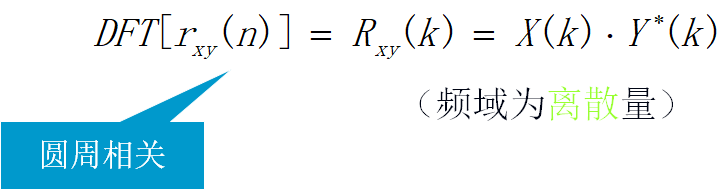
2）圆周卷积等于线性卷积的条件：

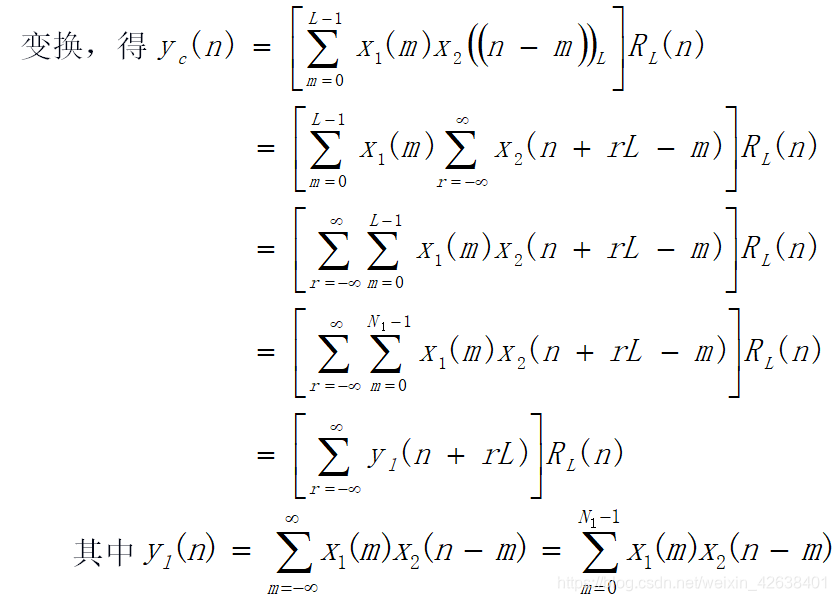
所以， 圆周卷积是线性卷积的周期延拓序列的主值序列。

圆周相关是线性相关的周期延拓序列的主值序列 

3） 线性卷积与圆周卷积关系的应用：

LSI系统的输出

卷积计算的运算量大，可利用卷积定理在频域相乘并作逆变换来求：