红黑树学习

一、红黑树简介

1972年Rudolf Bayer发明，称为平衡二叉B树（symmetric binary B-trees），在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为“红黑树”，一种特化的AVL树，在插入和删除时通过特定操作保持二叉查找树的相对平衡，从而获得较高的查找性能。

红黑树不是严格的AVL树，只是黑色平衡，如上图所示，根结点P的左子树显然比右子树高，但左子树和右子树的黑结点的层数是相等的。

二、红黑树特点

符合二叉搜索树基本特性，同时具备以下特性：

1. 节点非黑即红 （每个节点要么是黑色，要么是红色）
2. 其根节点是黑色
3. 叶子节点是黑色（为了简单期间，一般会省略该节点）
4. 相邻节点不同为红色（红色节点的子节点必是黑色）
5. 从一个节点到该节点的下叶子节点的所有路径上包含的黑节点数量相等（这一点是平衡的关键）

口决：黑根黑叶红不邻，同祖等高只数黑

三、红黑树接口方法

1. 查找节点
2. 左旋
3. 右旋
4. 插入节点
   • 七种情况处理
   • 五种情况需要考虑自平衡
5. 删除节点
   • 五种情况处理
   • 两种情况需要考虑自平衡（又细分八种情况，其中四种为镜像情况）

四、插入节点的七种情况

4.1 情况1

树为空直接创建红黑树

4.2 情况2

父节点为黑，直接添加子节点即可。子节点默认为红色节点。这种情况天生平衡。

4.3 情况3

父节点为红色、叔伯为红色。

4.4 情况4

父节点红色，叔伯黑色，爷爷、父亲、新节点形成ㄑ型

4.5 情况5

父节点红色，叔伯黑色，爷爷、父亲、新节点形成 / 型

4.6 情况6

父节点红色，叔伯黑色，爷爷、父亲、新节点形成 〉型

4.7 情况7

父节点红色，叔伯黑色，爷爷、父亲、新节点形成 \ 型

五、删除节点

查找位置、找替代节点、自平衡、真正删除

六、红黑树节点代码

class RBTreeNode {
	public int value;
	public boolean isRed;
	public RBTreeNode left;
	public RBTreeNode right;
	public RBTreeNode parent;
	
	public RBTreeNode(int value) {
		this.value = value;
		this.isRed = true; 
	}
	public RBTreeNode(int value, boolean isRed) {
		this.value = value;
		this.isRed = isRed;
	}
	// public boolean isRed() {
	// return isRed;
	// }
	public boolean isBlack() {
		return !isRed;
	}
}

七、红黑树的实现

7.1 查找节点

public RBTreeNode find(int value) {
	RBTreeNode node = root;
	//根据二叉搜索树的特点进行 查找
	while (node != null) {
		if (value == node.value) {//找到节点，返回
			return node;
		} else if (value < node.value) {//在左侧继续查找
			node = node.left;
		} else {//在右侧继续查找
			node = node.right;
		}
	}
	return null;
}

7.2 左旋

左旋左不变，与右互换放左边，右由右左来补全。

以某结点作为旋转结点，其右子结点变为旋转结点的父结点，右子结点的左子结点变为旋转结点的右子结点，左子结点保持不变。

1. 获取父节点、右子节点
2. 右子节点变为父节点的孩子
3. 右子节点变为旋转节点的父节点
4. 右子的左孩子变为旋转节点的右子
5. 旋转节点变为右子左孩子的父节点
6. 旋转节点变为右子节点的左孩子

public void leftRotate(RBTreeNode node) {
	RBTreeNode parent = node.parent;//父节点
	RBTreeNode right = node.right;//右节点
	
	if (parent == null) {//父节点为空，right成为根节点
		root = right; right.parent = null;
	} else {//设置父节点和right成为父子关系
		if (parent.left == node) parent.left = right;
		else parent.right = right;
		right.parent = parent;
	}
	
	node.parent = right;//right为node的父节点
	node.right = right.left;//right的左子树成为node的右子树
	if(right.left!=null)right.left.parent=node;//设置父节点
	right.left = node;//node 为 right 的左子节点
}

7.3 右旋

右旋右不变，与左互换放右边，左子左右来补全。

以某结点作为旋转结点，其左子结点变为旋转结点的父结点，左子结点的右子结点变为旋转结点的左子结点，右子结点保持不变。

1. 获取父节点、左子节点
2. 左子节点变为父节点的孩子
3. 左子节点变为旋转节点的父节点
4. 左子的右孩子变为旋转节点的左子
5. 旋转节点变为左子右孩子的父节点
6. 旋转节点变为左子节点的右孩子

public void rightRotate(RBTreeNode node) { 
	RBTreeNode parent = node.parent;//父节点
	RBTreeNode left = node.left;//左节点
	
	if (parent == null) {//父节点为空，left 成为根节点
		root = left;
		left.parent=null;
	} else {//设置父节点和 left 成为父子关系
		if (parent.left == node) parent.left=left;
		else parent.right=left;
		left.parent=parent;
	}
	
	node.parent=left;//left 为node的父节点
	node.left=left.right;//left的右子成为node的左子树
	if(left.right!=null)left.right.parent=node;//设置父节点
	left.right=node; // node 为 left 的右子节点
}

7.4 插入节点

1. 情况1：空树，新节点设为根结束
2. 查找插入位置（父节点）
3. 新节点挂到父节点下
4. 情况2：父节点为黑色，直接返回
5. 父节点为红色，需插入自平衡

public void insert(int value) {
	RBTreeNode node = new RBTreeNode(value);
	
	if (root == null) {//情况1：空树，新插入节点为根节点
		node.isRed=false;//根是黑色的
		root=node; return;
	}
	
	//新插入节点不是根节点，则需要查找待插入位置
	RBTreeNode position = root; RBTreeNode parent = null;
	boolean isLeftChild = false;
	while (position != null) {
		parent = position;
			if (value < parent.value) {
		position = parent.left; isLeftChild = true;
		} else if (value > parent.value) {
			position = parent.right; isLeftChild = false;
		} else {
			return; //已存在更新值，这里是整型数字直接返回
		}
	}
	
	//将新节点插入到对应父节点的下面
	if (isLeftChild) parent.left = node;
	else parent.right = node; 
	node.parent = parent; 
	
	if(parent.isBlack()) return; //情况2：父为黑色无需调整平衡
	balanceInsert(node); //父节点为红色，需要进行自平衡 调整
}

7.5 插入自平衡

父节点为红色循环处理

1. 获取爷爷、叔伯节点
2. 情况3：父红叔红，父黑叔黑爷变红，继续循环
3. 情况4：父红叔黑，爷父新成ㄑ型，左旋变情况5
4. 情况5：父红叔黑，爷父新成/型， 父黑爷红爷右旋
5. 情况6：父红叔黑， 爷父新成 〉型，右旋成情况7
6. 情况7：父红叔黑色，爷父新成\型，父黑爷红爷右旋保证根节点为黑色

private void balanceInsert(RBTreeNode node) {
	RBTreeNode parent, grandParent;
	
	while((parent=node.parent)!=null&&parent.isRed) {
		grandParent = parent.parent; //爷爷节点
		RBTreeNode uncle = grandParent.left; //叔伯节点
		if (uncle==parent) uncle = grandParent.right; 
		
		//情况3：父红叔红 父、叔转黑、爷转红
		if (uncle != null && uncle.isRed) {
			parent.isRed=false; uncle.isRed=false;
			grandParent.isRed=true;
			node = grandParent; 
			continue; //还要继续验证爷变红是否破坏平衡性
		}
		
		if (grandParent.left== parent) {//父为爷左子
			//情况4：父红叔黑，爷父新成 ㄑ ，左旋成情况5
			if (node == parent.right) { 
				leftRotate(parent); //以父节点为中心进行左旋
				RBTreeNode tmp=node; //node与parent交换
				node = parent; parent = tmp;
			}
			//情况5：父红叔黑，爷父新形成/ 父变黑爷变红爷右旋
			parent.isRed=false; grandParent.isRed=true;
			rightRotate(grandParent);//右旋
		} else {//父节点 为 爷爷节点的 右孩子
			//情况6：父红叔黑， 爷父新成 〉，右旋成情况7
			if (node == parent.left) { 
				rightRotate(parent); //以父节点为中心进行右旋
				RBTreeNode tmp = node; //node与parent 交换
				node = parent; parent = tmp;
			}
			//情况7：父红叔黑色，爷父新成\，父黑、爷红 爷右旋
			parent.isRed=false; grandParent.isRed=true;
			leftRotate(grandParent);//左旋
		}
	}
	//保证根节点为黑色
	root.isRed=false;
}

7.6 删除节点

1. 查找删除节点，不存在直接返回
2. 情况1：删除节点有两个字节点，用后继节点的值覆盖删除节点，删除节点变为后继节点
3. 优先选择左节点为替代节点
4. 存在替代节点
   情况2：删除节点为红色，直接替换掉删除节点
   情况3：删除节点为黑色，先替换删除节点再自平衡
5. 不存在替代节点
   情况4：删除节点为黑色，先做自平衡再删除
   情况5：删除节点为红色，直接删除

public void delete(int value) {
	RBTreeNode node = find(value); 
	if (node != null) deleteNode(node); //存在目标节点则删除
}
private void deleteNode(RBTreeNode node) {
	//情况1：有两个子节点找后继，后继的值给删除节点，视作删除后继
	if (node.left != null && node.right != null) {
		RBTreeNode s = successor(node); 
		node.value = s.value; 
		node = s;
	}
	//选择替代节点，优先选择左子节点补位
	RBTreeNode replacement=(node.left!=null?node.left:node.right);
	
	if (replacement != null) {
		//情况2将替代节点 提到当前删除节点的位置
		replacement.parent = node.parent;
		if (node.parent == null) root = replacement; //为根节点
		else if(node==node.parent.left)node.parent.left=replacement;
		else node.parent.right = replacement;//node为父的右节点
		node.left=node.right=node.parent=null; //node相关指针置空
	
		//情况3：删除节点为黑色，自平衡(替代节点变红)
		if (node.isBlack()) balanceDeletion(replacement); 
	} 
	else if(node.parent==null) {
		root=null;//删除节点为唯一节点
	} else {
		//情况4：无替代，节点为黑色，自平衡 删除节点变红
		if (node.isBlack()) balanceDeletion(node);
		
		//情况5：无替代，节点为红色，不破坏平衡 删除对该节点的相关引用
		if (node.parent != null) {
			if (node == node.parent.left) node.parent.left = null;
			else if(node==node.parent.right)node.parent.right=null;
			node.parent = null;
		}
	}
}

7.7 后继节

按中序遍历时的后一个节点

1. 存在右节点，找右节点分支上的最左侧的后辈节点
2. 不存在右节点，向上找作为后继节点的父辈节点, 直到自己所在分支是父节点的左节点

private RBTreeNode successor(RBTreeNode node) {
	if (node == null)
		return null;
	else if (node.right != null) {//存在右节点
		RBTreeNode p = node.right;
		while (p.left != null)//找右节点的最左侧的底层 孙节点
			p = p.left;
		return p;
	} else {
		//不存在右节点，向上找作为后继节点的父辈节点
		//直到自己所在分支是父节点的左节点
		RBTreeNode parent = node.parent;
		RBTreeNode curent = node;
		while (parent != null && curent == parent.right) {
			curent = parent;
			parent = parent.parent;
		}
		return parent;
	}
}

7.8 删除自平衡

节点为黑色循环处理

1. 情况1：为黑在左兄为红，父兄变色父左旋
2. 情况2：为黑在左兄为黑，侄子都为黑，兄变红向上验
3. 情况3：为黑在左兄为黑左侄红，兄侄变色兄右旋
4. 情况4：为黑在左兄为黑左侄不红，父兄变色父左旋，退循环
5. 情况5：为黑在右兄为红，父兄变色父右旋
6. 情况6：为黑在右兄为黑，侄子都为黑，兄变红向上验
7. 情况7：为黑在右兄为黑右侄红，兄侄变色兄左旋
8. 情况8：为黑在右兄为黑右侄不红，父兄变色父右旋，退循环
   节点变为黑色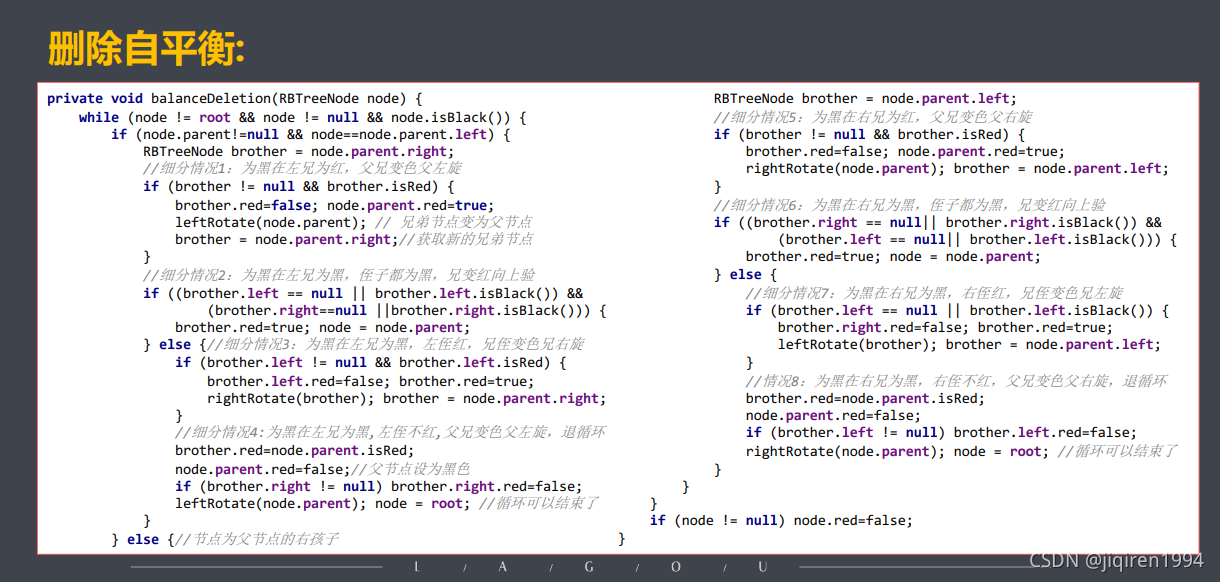
   

八、总结

红黑树插入和左旋右旋、变色平衡都能理解，但是删除自平衡就实在复杂多了，不过掌握了前面的也够用了。