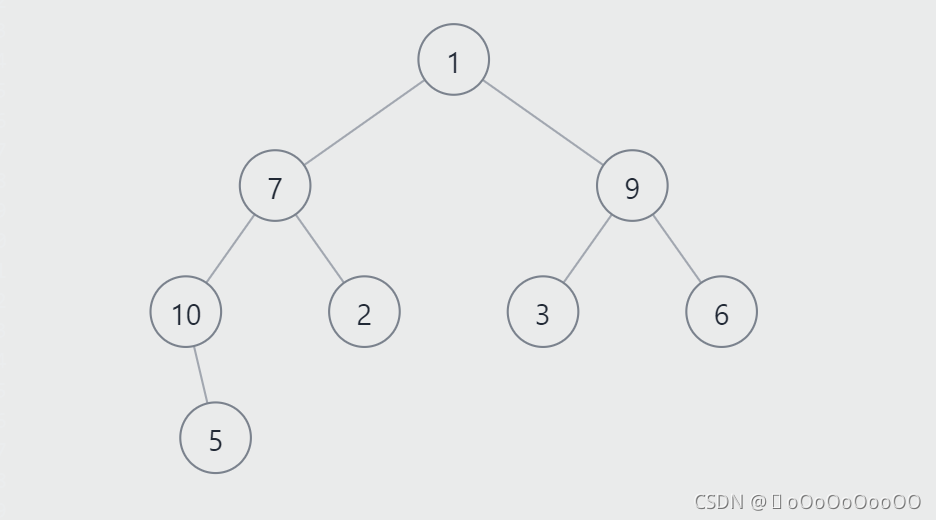
?‍?

?‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍??‍?

?‍?

这

是一颗普普通通的二叉树

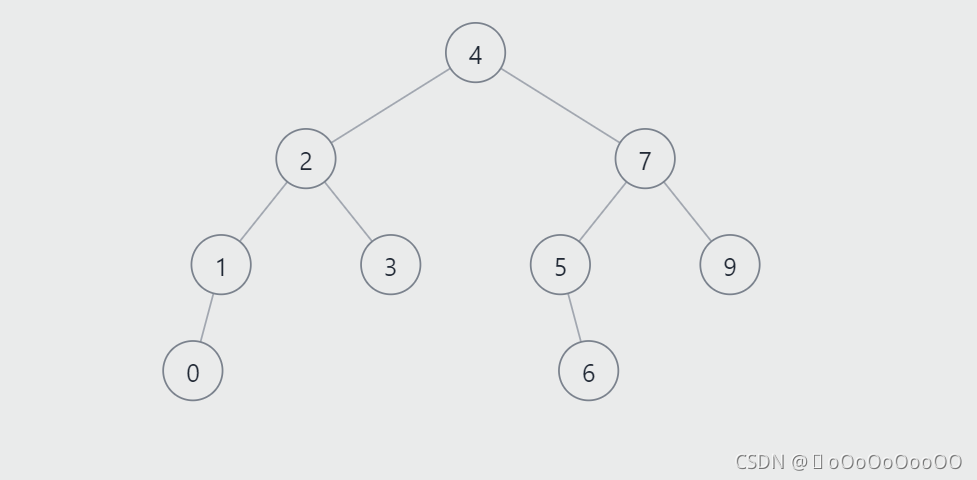
这

是一颗普普通通的二叉搜索树

 你

能发现它们两个之间有什么不同吗

我

不能?

但

你仔细一看?      哦   原来如此！

 ?二叉搜索树

1. 节点的左子树只包含 小于 当前节点的数

2. 节点的右子树只包含 大于 当前节点的数

3.所有左子树和右子树自身必须也是二叉搜索树

这就是二叉搜索树！

?创建二叉搜索树

?‍?在创建每个树之前，都需要先把节点定义好

public class TreeNode {
    public int val;
    public TreeNode left;
    public TreeNode right;
    public TreeNode(){}
    public TreeNode(int val){
        this.val = val;
    }
    public TreeNode(int val, TreeNode left, TreeNode right){
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

?‍?进行节点的插入

    public TreeNode insertIntoBST(TreeNode root, int val) {
        TreeNode node = new TreeNode(val);
        //root为null,表示初次进行二叉树的插入
        //则root 也就等于 node 节点
        if (root == null){
            root = node;
            return root;
        }
        //利用cur遍历二叉搜索树
        TreeNode cur = root;
        //标记父节点
        TreeNode pre = null;
        while(cur != null){
            //更新父节点
            pre = cur;
            //这里利用了二叉搜索树的定义
            //如果父节点的val小于插入节点的val, 则把插入的节点放到父节点的右支
            //如果父节点的val大于插入节点的val, 则把插入的节点放到父节点的左支
            if (cur.val > val){
                cur = cur.left;
            }else{
                cur = cur.right;
            }
        }
        //循环结束后,cur为空，pre此时为待插入的父节点
        //比较待插入节点的val和父节点val的大小
        //大则右，小则左
        if (pre.val > val){
            pre.left = node;
        }else{
            pre.right = node;
        }
        return root;
    }

?‍?如下一颗二叉搜索树，如果要插入的一个节点为6

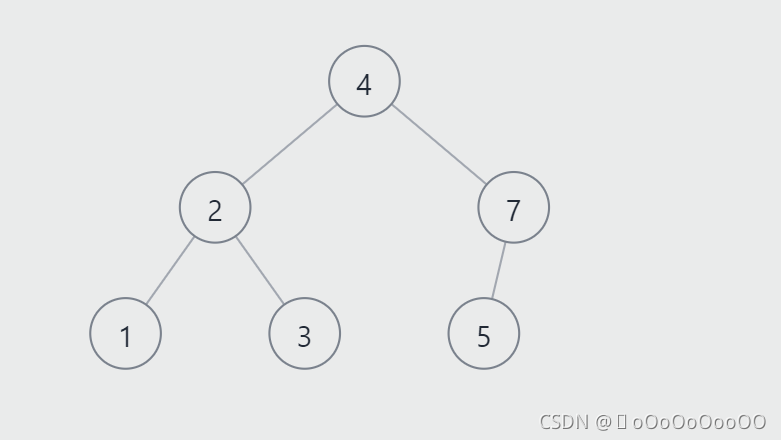
?‍? 6节点比5节点要大，使用要放在右支

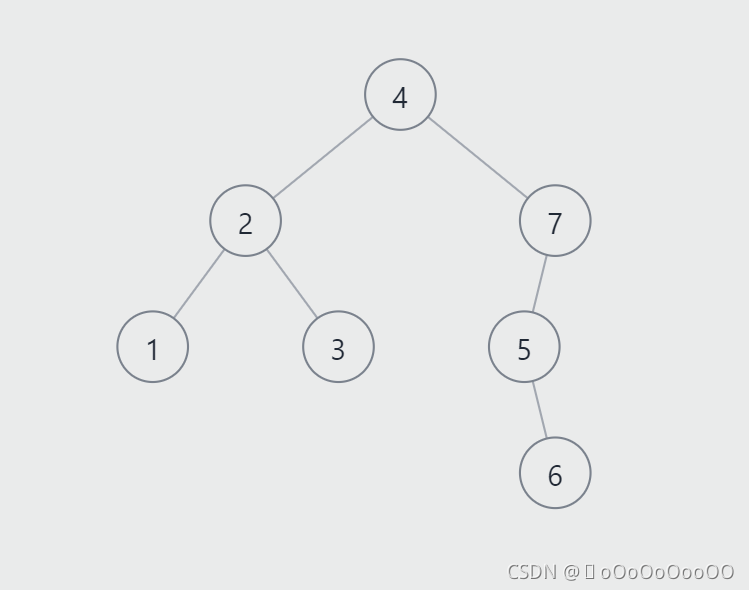
 ?‍?这就完成了对二叉搜索树的插入

不是说创建二叉搜索树吗，怎么说的是二叉搜索树的插入？

其实创建二叉搜索树就相当于对二叉搜索树进行一个个的插入操作

?二叉搜索树查找

?‍?找到则返回该节点，找不到则返回null

如果看到递归就头疼，建议多做一些关于递归的题目

    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null){
            return null;
        }
        //当前节点的val等于要查找的val，则直接返回该节点
        if (root.val == val){
            return root;
        }
        //当前节点的val大于要查找的val，则要对左子树进行查询
        if (root.val > val){
            return searchBST(root.left,val);
        }
        //当前节点的val小于要查找的val，则要对右子树进行查询
        return searchBST(root.right,val);
    }

?二叉搜索树删除

?‍?二叉搜索树最难的地方就在删除这一块

采用的方法为： 替罪?法

首先要明白的是：

要想删除该节点，则先要找到该节点，还有该节点的父节点

1.该怎么找到要删除的节点？

答：进行二叉树的查找 

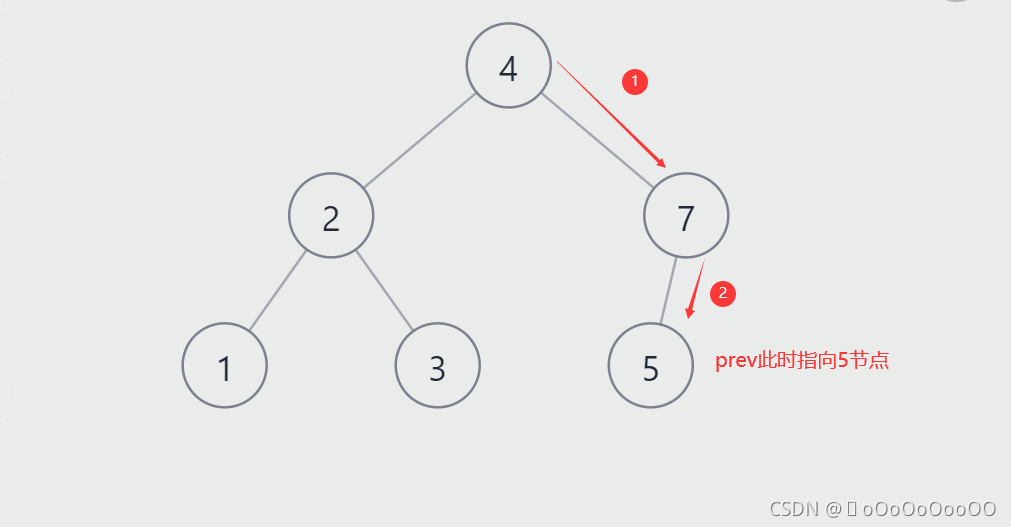
2.该怎么找到要删除节点的父节点？

答：定义个prev节点来追踪待删除节点的父节点

3.待删除的节点情况的分类？

答：从大的方向分 该节点为跟节点，该节点不为跟节点。

    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null){
            return null;
        }
        //待删除的节点
        TreeNode waitingDelete = root;
        //待删除节点的父节点
        TreeNode prev = null;
        while(waitingDelete != null &&waitingDelete.val != key){
            prev = waitingDelete;
            if (waitingDelete.val > key){
                waitingDelete = waitingDelete.left;
            }else{
                waitingDelete = waitingDelete.right;
            }
        }
        if (waitingDelete == null){
            return root;
        }
        //如果为跟节点
        if (prev == null){
            if (waitingDelete.right == null){
                //转头行动
                root = waitingDelete.left;
            }else{
                TreeNode cur = waitingDelete.right;
                if (cur.left == null){
                    cur.left = root.left;
                    root = cur;
                }else{
                    TreeNode preCur = null;
                    //这个循环结束后，就表明cur的左节点为null
                    while(cur.left != null){
                        preCur = cur;
                        cur = cur.left;
                    }
                    preCur.left = cur.right;
                    cur.left = waitingDelete.left;
                    cur.right = waitingDelete.right;
                    root = cur;
                }
            }
        }else{
            //不为根节点,这里有个问题:怎么判断待删除的节点是父节点的左节点还是右节点呢？
            if (waitingDelete.right == null){
                if (prev.left == waitingDelete){
                    prev.left = waitingDelete.left;
                }else{
                    prev.right = waitingDelete.left;
                }
            }else{
                TreeNode cur = waitingDelete.right;
                if (cur.left == null){
                    cur.left = waitingDelete.left;
                    if (prev.left == waitingDelete){
                        prev.left = cur;
                    }else{
                        prev.right = cur;
                    }
                }else{
                    TreeNode preCur = null;
                    while(cur.left != null){
                        preCur = cur;
                        cur = cur.left;
                    }
                    preCur.left = cur.right;
                    cur.left = waitingDelete.left;
                    cur.right = waitingDelete.right;
                    if (prev.left == waitingDelete){
                        prev.left = cur;
                    }else{
                        prev.right = cur;
                    }
                }
            }
        }