卡尔曼滤波学习笔记(Kalman filter)
学习基于:卡尔曼滤波器教程与MATLAB仿真
一、 为什么使用卡尔曼滤波器
例:火箭燃烧腔温度测量,温度太高无法测量,只能在附近点间接测量,数据将叠加噪声干扰
测量汽车位置,用IMU、GPS、Odometer融合,如何融合
二、了解卡尔曼滤波器——状态观测器
由于观测器方程的参数不可能与实际系统完全一致,所以估计的x会越来越偏离实际值,需要在观测器的状态方程中引入一项观测器输出和实际输出的误差项加以补偿,观测器增益矩阵为K,是一个待定的矩阵
e o b s = x − x ^ x ˙ = A x + B u x ^ ˙ = A x ^ + B u + K ( y − y ^ ) e ˙ o b s = ( A − K C ) e o b s e o b s ( t ) = e ( A − K C ) t e o b s ( 0 ) e_{obs} = x-\hat x \\\dot x= Ax+Bu\\\dot {\hat x}=A\hat x+Bu+K(y-\hat y) \\ \dot e_{obs}=(A-KC)e_{obs} \\ e_{obs}(t)=e^{(A-KC)t}e_{obs}(0)eobs=x−x^x˙=Ax+Bux^˙=Ax^+Bu+K(y−y^)e˙obs=(A−KC)eobseobs(t)=e(A−KC)teobs(0)
三、了解卡尔曼滤波器——最优状态估计
原系统在状态方程和输出方程中都会有噪声,动态结构图如下
v ∼ N ( 0 , R ) w ∼ N ( 0 , Q ) v \sim N(0,R) \\ w \sim N(0,Q)v∼N(0,R)w∼N(0,Q)
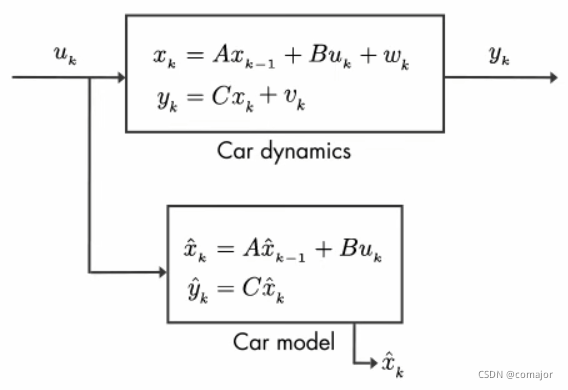
图1 观测器的动态结构图
其中输入u k u_kuk和输出y k y_kyk分别代表速度和位置,w k w_kwk表示过程噪声(process noise),v k v_kvk表示测量噪声(measurement noise),它们假设都是服从高斯分布的噪声
optimal state estimate是把x ^ k \hat x_kx^k和y k y_kyk的估计函数相加得到的,它本身也是一个高斯噪声的形式
四、最优状态估计算法和方程
卡尔曼滤波器是状态观测器的一种,但是它是针对于随机系统(stochastic systems)设计的
Kalman filter: $ {\hat x}k=A\hat x{k-1}+Bu+K_k(y_k-C(A\hat x_{k-1}+Bu_k))$
Priori Estimate 先验估计:x ^ k − = A x ^ k − 1 + B u k \hat x_k^- = A\hat x_{k-1}+Bu_kx^k−=Ax^k−1+Buk
这样方程式可以重写为: x ^ k = x ^ k − ⏟ p r e d i c t + K k ( y k − C x k − ) ⏟ u p d a t e \hat x_k=\underbrace{\hat x_{k}^-}_{predict}+\underbrace{K_k(y_k-Cx_{k}^-)}_{update}x^k=predictx^k−+updateKk(yk−Cxk−)
可以理解为下一时刻的状态估计(后验估计)等于先验状态估计和基于输出的状态估计更新的一个综合
Posteriori Estimate 后验估计: x ^ k \hat x_kx^k
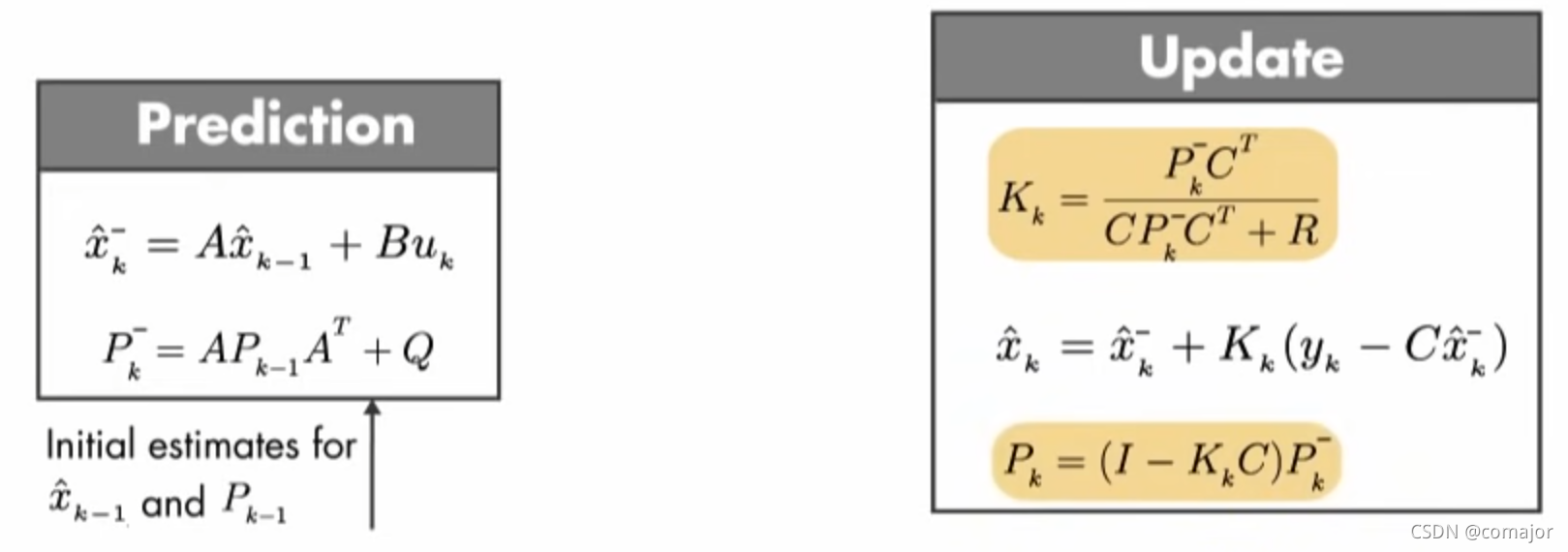
图2 卡尔曼滤波器的迭代公式
P k − P_k^-Pk−:The variance of the priori estimate 先验估计x ^ k − \hat x_k^-x^k−的方差
P k P_kPk:Error covariance 误差方差
K k K_kKk:Kalman gain 卡尔曼增益用于调节先验估计和测量值两者体现在最优估计中的比例
考虑一个极端的情况,当测量噪声的方差R趋向于0的时候,滤波器将更相信测量值y k y_kyk:
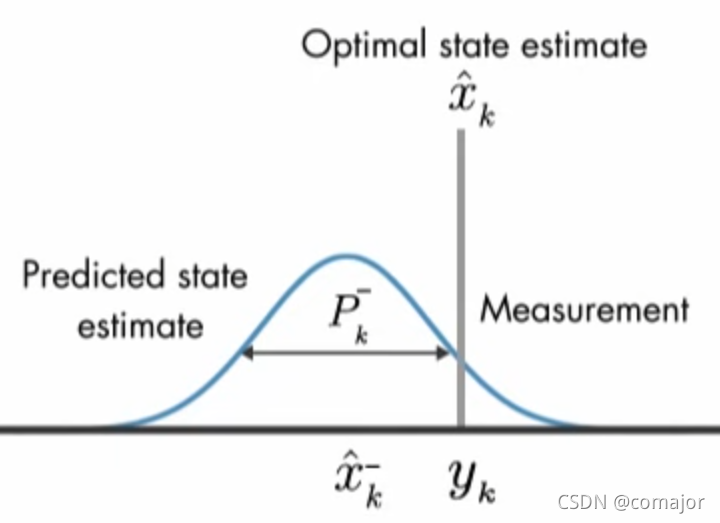
图3 测量误差为零的时候,估计值直接使用测量值变换得到
与之对应的另外一个极端情况,当过程噪声的方差Q趋向于0的时候,滤波器将更相信先验估计值x ^ k − \hat x_k^-x^k−:
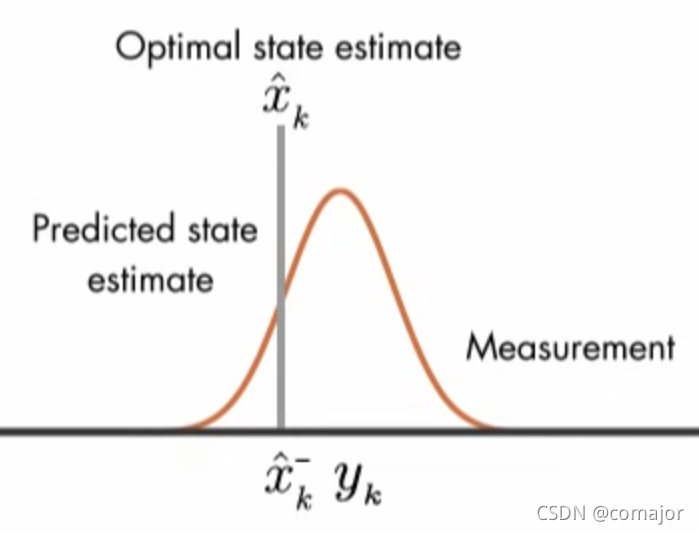
图4 过程误差为零的时候,估计值直接使用先验估计
五、非线性状态估算器
这一章介绍四个其他的滤波器,他们有各自的特定和应用场合
Kalman filter只适用于线性系统,对于非线性系统
x k = f ( x k − 1 , u k ) + w k y k = g ( x k ) + v k x_k=f(x_{k-1},u_k)+w_k \\ y_k = g(x_k)+v_kxk=f(xk−1,uk)+wkyk=g(xk)+vk
将系统线性化后可以用EKF(extended Kalman filter)
线性化过程如下(Nonlinear transformation)
Δ x k ≈ F Δ x k − 1 + w k Δ y k ≈ G Δ x k + v k F = ∂ f ∂ x ∣ x ^ k − 1 , u k G = ∂ g ∂ x ∣ x ^ k \Delta x_k \approx F\Delta x_{k-1}+w_k \\ \Delta y_k \approx G\Delta x_k +v_k \\ \qquad F = \frac{\partial f}{∂x}\bigg\rvert_{\hat x_{k-1},u_k}\\ G = \frac{\partial g}{∂x}\bigg\rvert_{\hat x_{k}}Δxk≈FΔxk−1+wkΔyk≈GΔxk+vkF=∂x∂f∣∣∣∣x^k−1,ukG=∂x∂g∣∣∣∣x^k
Drawbacks to Using Extended Kalman Filters(EKFS)
- It is difficult to calculate the Jacobians (if they need to be found analytically) 偏导有时难以用解析的方式计算
- There is a high computational cost(if the Jacobians can be found numerically) 即使采用数值的方式近似计算也需要很大的计算资源
- EKF only works on systems that have a differentiable model 要求系统必须可以求导
- EKF is not optimal if the system is highly nonlinear 如果系统是强非线性系统,可能无法使用EKF
Unscented Kalman Filters(UKF)
approximate the probability distribution
取一组采样点,数量达到足以估计出高斯分布的均值和方差,分别状态估计计算后得到经验高斯分布
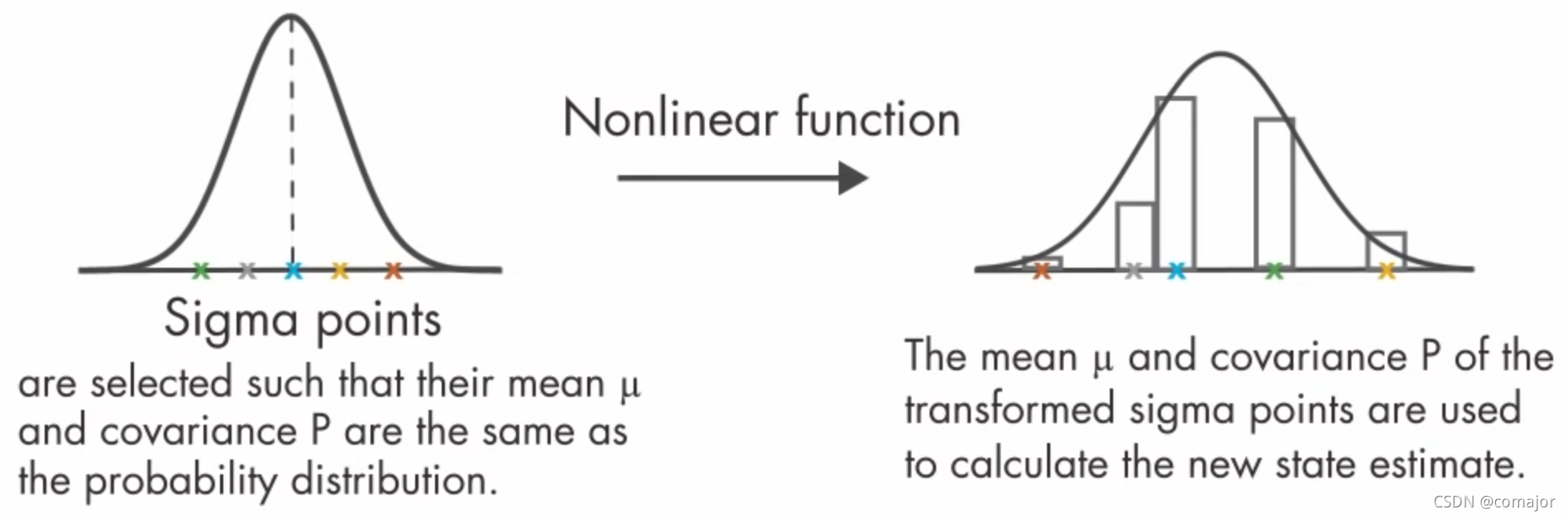
图5 UKF过程示意
Particle filter(PF)
相较于UKF需要假设状态高斯分布,PF可以应用于任意分布,同时也必然需要采集更多的采样点
至此,四种滤波器的主要分别集中在主要在适用模型、状态分布假设和计算量上,列表如下
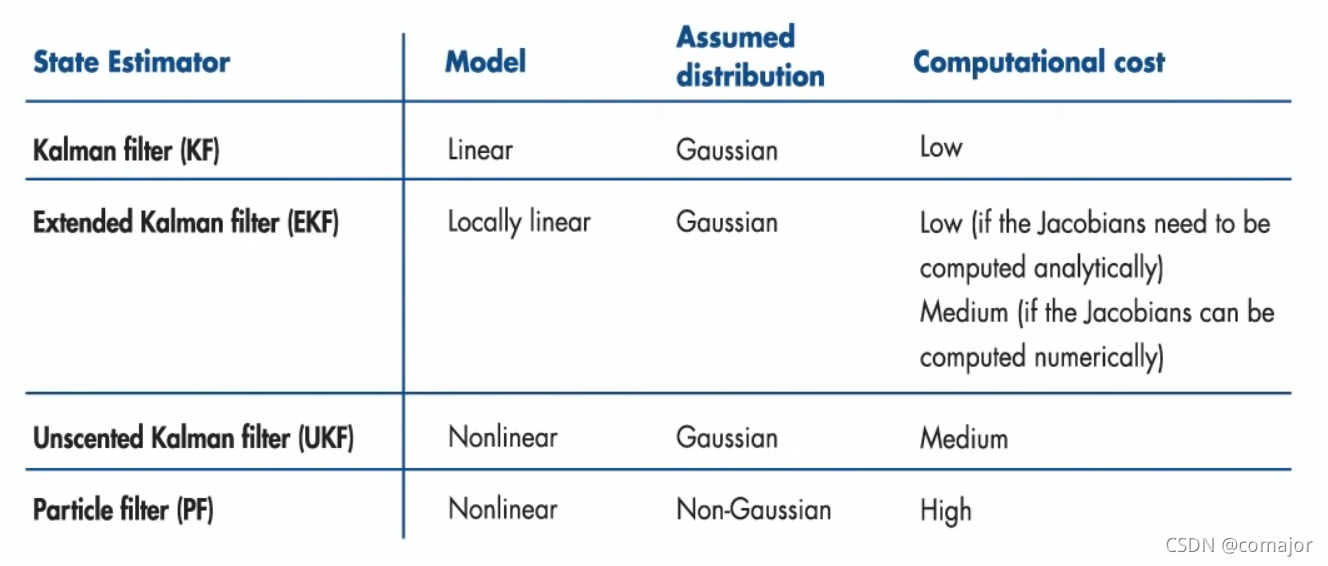
图6 各种滤波器的比较
六、其他
一些MATLAB/Simulink使用卡尔曼滤波器的教程网站,供学习:
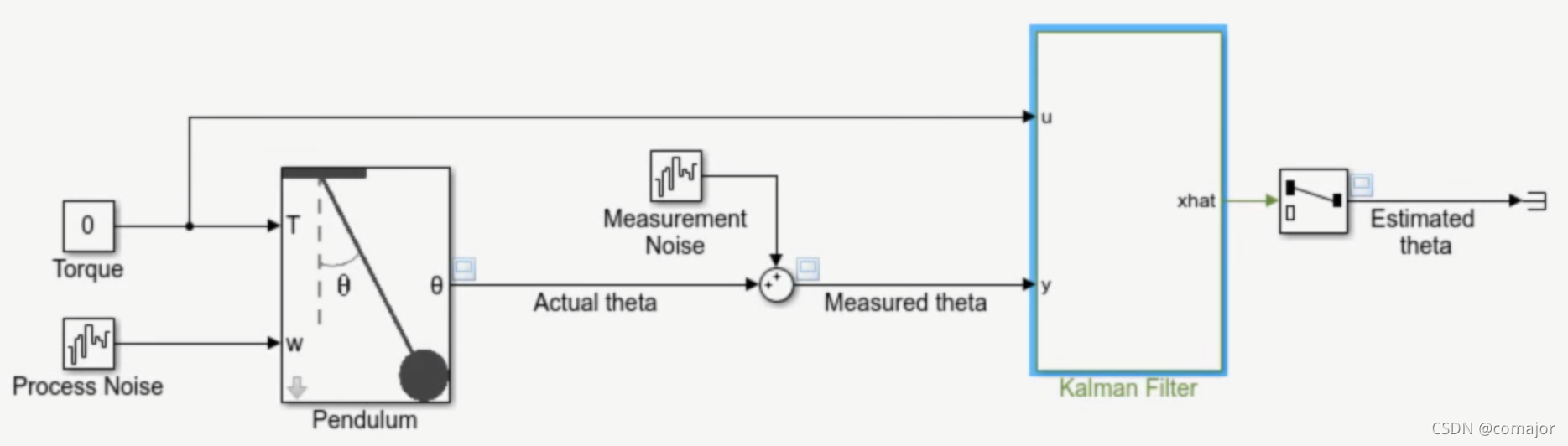
图7 Simulink卡尔曼滤波实验