一、实验目标
1、使用 K-means 模型进行聚类,尝试使用不同的类别个数 K,并分析聚类结果。
2、按照 8:2 的比例随机将数据划分为训练集和测试集,至少尝试 3 个不同的 K 值,并画出不同 K 下 的聚类结果,及不同模型在训练集和测试集上的损失。对结果进行讨论,发现能解释数据的最好的 K 值。二、算法原理
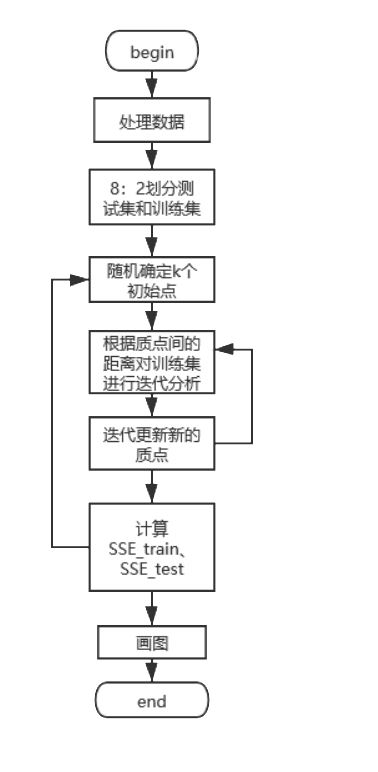
首先确定k,随机选择k个初始点之后所有点根据距离质点的距离进行聚类分析,离某一个质点a相较于其他质点最近的点分配到a的类中,根据每一类mean值更新迭代聚类中心,在迭代完成后分别计算训 练集和测试集的损失函数SSE_train、SSE_test,画图进行分析。
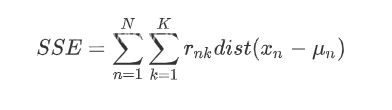
伪代码如下: num=10 #k的种类
for k in range(1,num):
随机选择k个质点
for i in range(n): #迭代n次
根据点与质点间的距离对于X_train进行聚类
根据mean值迭代更新质点
计算SSE_train
计算SSE_test
画图
算法流程图:
三、代码实现
1、导入库 import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
2、计算距离 def distance(p1,p2):
return np.sqrt((p1[0]-p2[0])**2+(p1[1]-p2[1])**2)
3、计算均值 def means(arr):
return np.array([np.mean([p[0] for p in arr]),np.mean([p[1] for p in arr])])
4、二维数据处理 #数据处理
data= pd.read_table('cluster.dat',sep='\t',header=None)
data.columns=['x']
data['y']=None
for i in range(len(data)): #遍历每一行
column = data['x'][i].split( ) #分开第i行,x列的数据。split()默认是以空格等符号来分割,返回一个列表
data['x'][i]=column[0] #分割形成的列表第一个数据给x列
data['y'][i]=column[1] #分割形成的列表第二个数据给y列
list=[]
list1=[]
for i in range(len(data)):
list.append(float(data['x'][i]))
list.append(float(data['y'][i]))
list1.append(list)
list=[]
arr=np.array(list1)
print(arr)
5、划分数据集和训练集 #按照8:2划分数据集和训练集
X_train, X_test = train_test_split(arr,test_size=0.2,random_state=1)
6、主要聚类实现 count=10 #k的种类:1、2、3...10
SSE_train=[] #训练集的SSE
SSE_test=[] #测试集的SSE
n=20 #迭代次数
for k in range(1,count):
cla_arr=[] #聚类容器
centroid=[] #质点
for i in range(k):
j=np.random.randint(0,len(X_train))
centroid.append(list1[j])
cla_arr.append([])
centroids=np.array(centroid)
cla_tmp=cla_arr #临时训练集聚类容器
cla_tmp1=cla_arr #临时测试集聚类容器
for i in range(n): #开始迭代
for e in X_train: #对于训练集中的点进行聚类分析
pi=0
min_d=distance(e,centroids[pi])
for j in range(k):
if(distance(e,centroids[j])
min_d=distance(e,centroids[j])
pi=j
cla_tmp[pi].append(e) #添加点到相应的聚类容器中
for m in range(k):
if(n-1==i):
break
centroids[m]=means(cla_tmp[m])#迭代更新聚类中心
cla_tmp[m]=[]
dis=0
for i in range(k): #计算训练集的SSE_train
for j in range(len(cla_tmp[i])):
dis+=distance(centroids[i],cla_tmp[i][j])
SSE_train.append(dis)
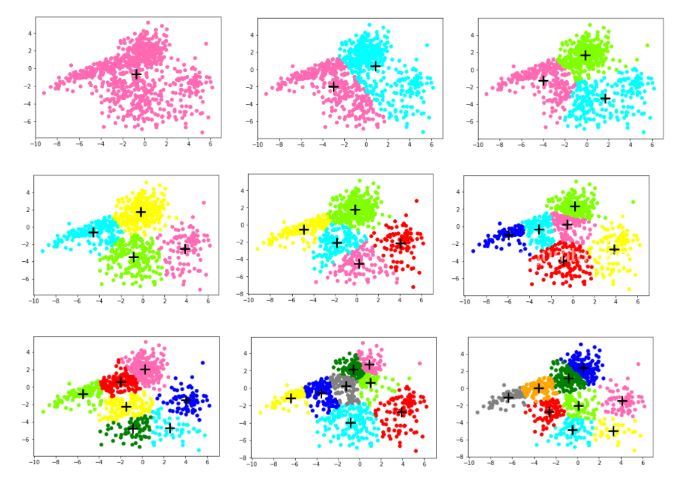
col = ['HotPink','Aqua','Chartreuse','yellow','red','blue','green','grey','orange'] #画出对应K的散点图
for i in range(k):
plt.scatter([e[0] for e in cla_tmp[i]],[e[1] for e in cla_tmp[i]],color=col[i])
plt.scatter(centroids[i][0],centroids[i][1],linewidth=3,s=300,marker='+',color='black')
plt.show()
for e in X_test: #测试集根据训练集的质点进行聚类分析
ki=0
min_d=distance(e,centroids[ki])
for j in range(k):
if(distance(e,centroids[j])
min_d=distance(e,centroids[j])
ki=j
cla_tmp1[ki].append(e)
for i in range(k): #计算测试集的SSE_test
for j in range(len(cla_tmp1[i])):
dis+=distance(centroids[i],cla_tmp1[i][j])
SSE_test.append(dis)
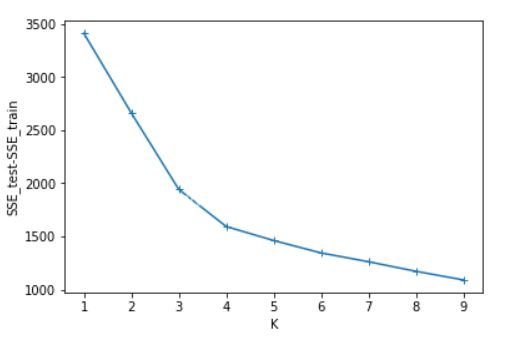
7、画图 SSE=[] #计算测试集与训练集SSE的差值
for i in range(len(SSE_test)):
SSE.append(SSE_test[i]-SSE_train[i])
x=[1,2,3,4,5,6,7,8,9]
plt.figure()
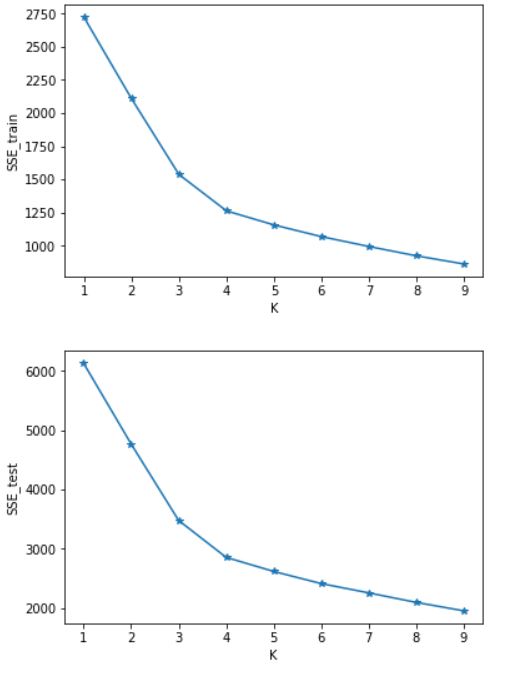
plt.plot(x,SSE_train,marker='*')
plt.xlabel("K")
plt.ylabel("SSE_train")
plt.show() #画出SSE_train的图
plt.figure()
plt.plot(x,SSE_test,marker='*')
plt.xlabel("K")
plt.ylabel("SSE_test")
plt.show() #画出SSE_test的图
plt.figure()
plt.plot(x,SSE,marker='+')
plt.xlabel("K")
plt.ylabel("SSE_test-SSE_train")
plt.show() #画出SSE_test-SSE_train的图
四、实验结果分析
可以看出SSE随着K的增长而减小,测试集和训练集的图形趋势几乎一致,在相同的K值下,测试集的SSE大于训练集的SSE。于是我对于在相同的K值下的SSE_test和SSE_train做了减法(上图3),可知K=4时数据得出结果最好。这里我主要使用肘部原则来判断。本篇并未实现轮廓系数,参考文章:https://www.jb51.net/article/187771.htm
总结
到此这篇关于python 代码实现k-means聚类分析(不使用现成聚类库)的文章就介绍到这了,更多相关python k-means聚类分析内容请搜索聚米学院以前的文章或继续浏览下面的相关文章希望大家以后多多支持聚米学院!