【动态规划入门】斐波拉契

动态规划问题的一般形式就是求最值，核心问题是穷举。因为要求最值，肯定要把所有可行的答案穷举出来，然后在其中找最值。动态规划的穷举有点特别，因为这类问题存在「重叠子问题」，如果暴力穷举的话效率会极其低下，所以需要「备忘录」或者「DP table」来优化穷举过程，避免不必要的计算。而且，动态规划问题一定会具备「最优子结构」。要符合「最优子结构」，子问题间必须互相独立。

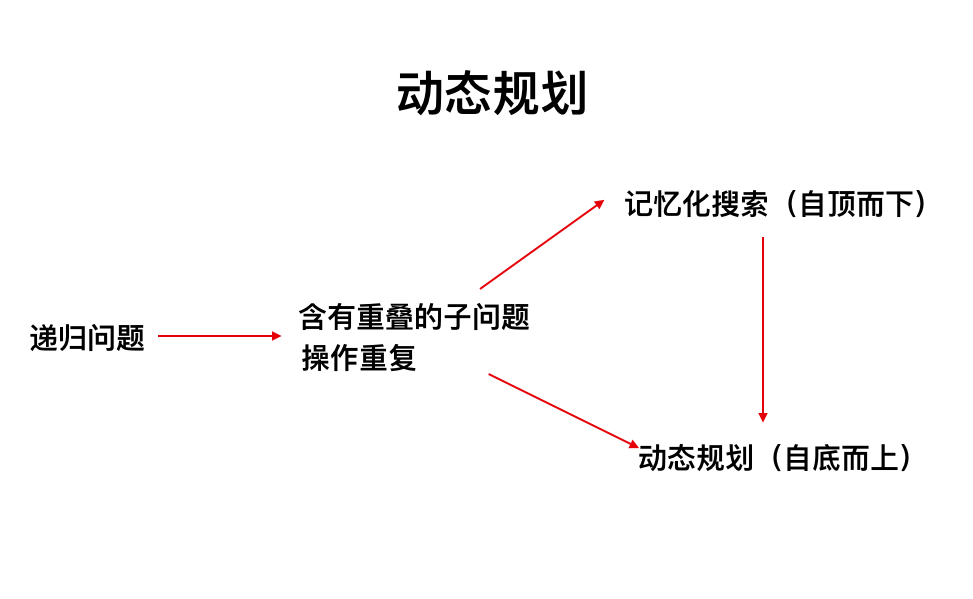
关键词：递归（穷举）、求最值、重叠子问题

1、暴力递归

#include<iostream>
using namespace std;
const int maxn = 10010;
int fib(int n) {
	if (n == 1 || n == 2)	return	1;
	return fib(n - 1) + fib(n - 2);
}
int main() {
	int a;
	cin >> a;
	cout << fib(a);
	system("pause");
	return 0;
}