PC_溢出概念+判断方法+示例

• 算术溢出（arithmetic overflow）是指计算机进行算术运算产生的结果超出机器所能表示的范围。

ref

• 计组_浮点数表示/定点数和浮点数比较/溢出_xuchaoxin1375的博客-CSDN博客_浮点数的补码怎么算

分类

• 根据溢出方向:

  • 上溢

  • 下溢

  • 在浮点机中可以进一步分为:

    • 正上溢

    • 负上溢

    • 正下溢

    • 负下溢

    • 正下溢和负下溢是连在一起的区间(是0的去心邻域)

      • 浮点数可以表达0,但是可能表示不了不等于但是很接近0的数

• 根据小数点类型:

  • 定点机定点数溢出
  • 浮点机浮点数溢出

定点计算机中的溢出

• 从正方向超过了数的表示范围，称为上溢；
• 从负方向超过了数的表示范围，则称为下溢。

定点机溢出示意图

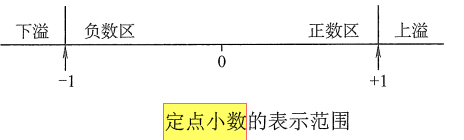
• 定点数小数的溢出示意
  • 可见,定点小数只可以表示纯小数
    • 否则会上溢

• 定点整数溢出:
  • 定点整数只能够表示纯整数,否则会出现下溢

在浮点计算机中的溢出

• 浮点数的表示范围主要由阶码来决定。(尾数决定的是精度)

• 不论数的符号是正还是负，若阶码从正的方向超出了阶码的表示范围，称为上溢；

• 若阶码从负的方向超出阶码的表示范围，或者尾数为“0”时，统称为下溢。

浮点机溢出示意图

• 一般来说，计算机对于浮点数的下溢，则自动当作“0”来处理，不输出错误信息(精度的溢出)；

• 而产生的上溢(范围溢出)，计算机则产生==“溢出中断”==，并输出溢出的错误信息，甚至停止程序的运行

溢出简易判断规律

• 定点数加减运算结果出现溢出时,得到的是错误的结果

溢出的必要条件

• 仅当两个符号相同的数相加或两个符号相异的数相减才可能产生溢出

  • 上面两种情况才有可能引发进位

    • (换句话说,如果两个参与计算的数(本身没有溢出)且计算过程没有进位,则该计算也不可能发生溢出)

      • 进位是溢出的必要条件

    • 但是如果只知道发生了进位,不可以断定发生溢出

      • 设机器数$S=x_0,x_1{x}_2\cdots x_n$

      • 更有具体的是,最高位数值位$x_1$处发生进位(以原码为例)

  • 口诀:同号加,异号减,进位是发生溢出的必要条件

    • 比如:两个正数相加，结果的符号位却为 1 (结果为负);

    • 一个负数减去某个正数，结果的符号位却为 0 (结果为正)

定点数?补码运算判断溢出方法

• 方法使用对象:定点数补码
  • 定点数补码的加减运算溢出判断的方法有 3 种:

用一位符号位判断溢出

• 对于加法

  • 只有在正数加正数和负数加负数两种情况下才可能出现溢出,
  • 符号不同的两个数相加是不会溢出的。

• 对于减法

  • 只有在正数减负数或负数减正数两种情况下才可能出现溢出,
  • 符号相同的两个数相减是不会溢出的。

• 而减法运算在及其中是用加法器实现的,无论是加法还是减法:

  • 只要参与操作的2个数A,B的符号$A_s,B_s$相同(AB>0)

  • 再将机器的计算结果记为S,S的符号位记为$S_s$

  • 溢出的条件就是:

    • $A_s,B_s的符号位(相同且)都与S_s相反$

      • 使用数字逻辑表达式进行描述:

        • $A_s{B}_s{S}_s$
          • 110
          • 001
        • 使用卡诺图等方法可以推导出相应的逻辑表达式

      • $$\begin{gathered} V=A_s{B}_s\overline{S_s}+\overline{A_s}\overline{B_s}{S}_s \\ 如果V=0表示无溢出 \\ 否则溢出 \end{gathered}$$

    • 从概率论的角度看,事件$V=\{发生溢出\}$的符号表示为:

      • $V=A_s{B}_s\overline{S_s}\cup \overline{A_s}\overline{B_s}{S}_s$
        • $V_1=A_s{B}_s\overline{S_s}$
        • $V_2=\overline{A_s}\overline{B_s}{S}_s$
        • $V=V_1\cup V_2,V_1与V_2至少一个事件发生,则表示溢出$

例

• 下面以机器字长为4位(含1位符号位)为例,说明机器是如何判断溢出的。

• 机器字长为4位的补码所对应的真值范围为-8~+7,运算结果一旦超过这个范围即为溢出。

  • 由于减法运算在机器中是用加法器实现的,因此可得出如下结论:不论是作加法还是减法，只要实际参加操作的两个数符号相同,结果又与原操作数的符号不同,即为溢出。
  • 

例

上例化为十进制时,真值运算表示($-\frac{1}{2}+(-\frac{1}{2}))=-1$

由$[A+B{]}_{补码}$= 1.0000,而且对应的真值:A + B= - 1,由此可见,用补码表示定点小数时,它能表示–1的值。

• 计算机中采用1位符号位判断时,为了节省时间,通常用符号位产生的进位与最高有效位产生的进位异或操作后,按其结果进行判断。
• (若异或结果为1 ,即为溢出;异或结果为0,则无溢出。
• 例6.12中符号位有进位(1),最高有效位无进位(0),即$1\oplus 0=1$,故溢出。
• 例6.13中符号位有进位(1),最高有效位也有进位(1),即$1\oplus 1=0$,故无溢出。

双符号位:变形补码判断溢出

• $$\begin{gathered} 变形补码,又称为模4补码(\mathrm{mod}4) \\ 双符号位的补码小数定义为: \\ DC(x)=[x{]}_{补}=\{\begin{array}{ll}x,& 0⩽x<1\\ 4+x=4-|x|,& -1⩽x<0\end{array}(\mathrm{mod}4) \\ 模4补码双符号位中:00表示正,11表示负 \\ 用在ALU中 \end{gathered}$$

• 变形补码判断溢出的原则是:

  • 当2位符号位不同时,表示溢出,

    • 计算结果的实际(正确)符号和溢出的正负性(正溢出/负溢出)都取决于第一位符号位)
      • 00
      • 01(正溢出)
      • 10(负溢出)
      • 11

  • 否则,无溢出。

• 不论是否发溢出,高位(第1位)符号位永远代表真正的符号。

• 逻辑表达式

  • 将结果S的第一位和第二位符号位分别表示为$S_{S_1},S_{S_2}$

  • $$V=S_{S_1}\oplus S_{S_2}$$

    • 结果为1表示溢出否则没有溢出

例

• 此时,符号位为“01”,表示溢出,又因第1位符号位为“0”,表示结果的真正符号为正,故“01”表示正溢出。

例

• 符号位为“10”,表示溢出。由于第1位符号位为1 ,则表示负溢出。
  上述结论对于整数也同样适用。
• 在浮点机中,当阶码用两位符号位表示时,判断溢出的原则与小数的完全相同。

硬件实际情况

• 采用双符号位方案时,寄存器和主存中的操作数符号仍然只需要保留一位
• 关键在于加法器中的符号位是两位
  • 在相加时,寄存器中的操作数的一位符号值$X_s$需要同时传送到加法器的两位符号位的输入端即可

采用一位符号位并根据最高数据位进位情况判断

• 参与计算的2个数A,B的

  • 符号位分别记为$A_s,B_s$
  • 最高数值位分别记为$a_1=A_{x_1},b_1=B_{x_1}$
  • $C_s=A_s+B_s+C_1$
  • $C_1=Carry(a_1+b_1+C_2)$
    • $C_i=Carry(a_i+b_i+C_{i-1})$
      • $\cdots$
      • $假设机器字长为n+1(数值为部分n位:x_1\cdots x_n)$
      • $C_{n-1}=Carry(a_{n-1}+b_{n-1}+C_n)$
      • $C_n=Carry(a_n+b_n)$
      • $这里Carry(\sum p_i)函数是取进位函数的意思(对于二进制,其取值结果只有0/1两种可能)$

• 如果符号位的进位$C_s$与最高数值为的进位$C_1$相同,说明没有溢出

  • 否则表示你溢出

• 溢出判断逻辑表达式

  • $$\begin{gathered} V=C_s\oplus C_1 \\ 如果V=0,无溢出 \\ 否则溢出 \end{gathered}$$