大数乘法和大数加法(正整数)

最近在学数据结构,看到有一个求级数的问题

 一开始我觉着很简单,然后就直接用long long int 求了,发现所得的数字太大了,就会溢出.

然后发现这道题得用字符串来存数字.

写了字符串的加法和乘法

加法用模10进位就好了.

乘法要考虑数字位数的问题:

数组的第[i]位和第[j]位相乘,所得结果数组对应[i+j]位和[i+j+1]位置,用123*45为例:

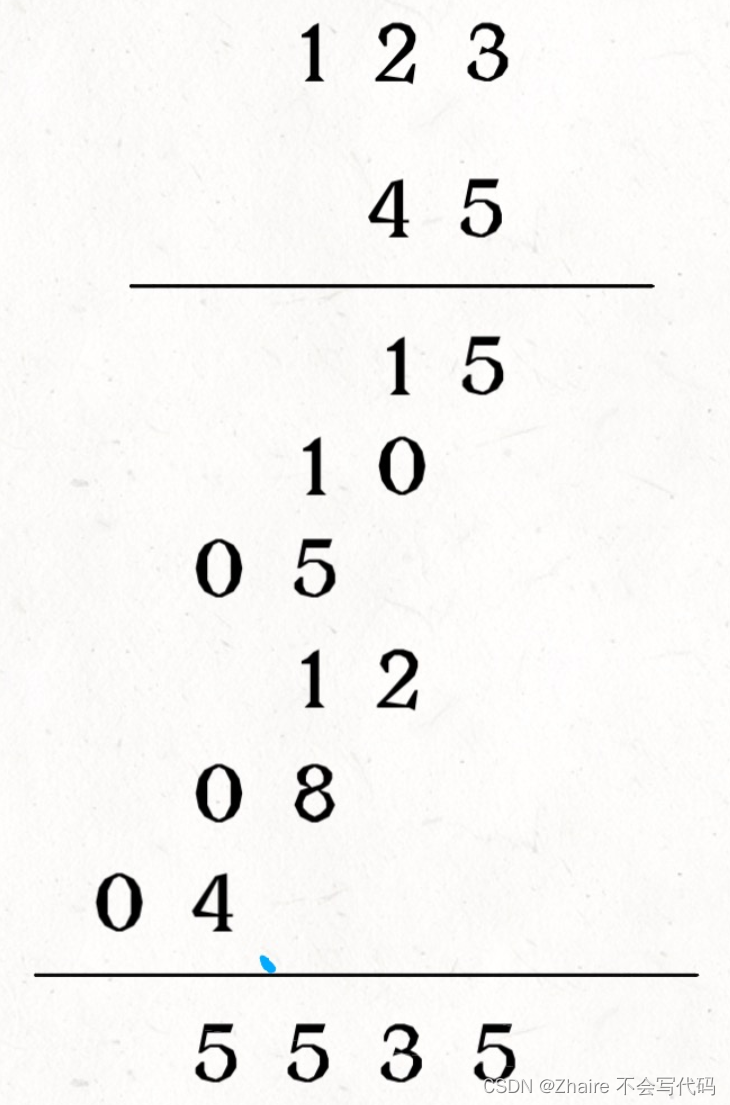
用倒查法装入数组,整个逻辑会简单一点.

//大数加法,返回字符串
string Add(string NumA, string NumB)
{
    string NumAns;//定义结果数组
    //倒叙插入让个位补齐
    int NumberA[MAX] = { 0 };
    int NumberB[MAX] = { 0 };//用两个超大的数组装
    int NumberAns[MAX] = { 0 };//答案数组

    int LengthNumA = int(NumA.size());
    int LengthNumB = int(NumB.size());//把数组长度求得这个很有用

    for (int i = 0; i < LengthNumA; i++)
        NumberA[i] = NumA[LengthNumA - 1 - i] - '0';

    //倒叙插入补齐个位,并且让字符串变成可以运算的整数
    for (int i = 0; i < LengthNumB; i++)
        NumberB[i] = NumB[LengthNumB - 1 - i] - '0';

    int Ans_Length = LengthNumA > LengthNumB ? LengthNumA : LengthNumB;
    //答案串的长度,进位再另说

    for (int i = 0; i < Ans_Length; i++)
    {
        NumberAns[i] += NumberA[i] + NumberB[i];//先加了,后面会考虑进位的情况
        NumberAns[i + 1] += (NumberAns[i]) / 10;//进一的情况
        NumberAns[i] %= 10;//考虑进位的情况
    }
    //去除前面的0,缩短Ans_Length;

    if (NumberAns[Ans_Length])//进位了;
        Ans_Length++;

    for (int i = Ans_Length - 1; i >= 0; i--)//装填到字符串里面
        NumAns += NumberAns[i] + '0';
    return NumAns;
}

//大数乘法,返回字符串
string Muti(string NumA, string NumB)
{
    if (NumA == "0" || NumB == "0")
    {
        return "0";
    }
    string NumAns;//定义结果数组
    //倒叙插入让个位补齐
    int NumberA[MAX] = { 0 };
    int NumberB[MAX] = { 0 };//用两个超大的数组装
    int NumberAns[MAX] = { 0 };//答案数组

    int LengthNumA = int(NumA.size());
    int LengthNumB = int(NumB.size());//把数组长度求得这个很有用

    //倒叙插入补齐个位,并且让字符串变成可以运算的整数
    for (int i = 0; i < LengthNumA; i++)
        NumberA[i] = NumA[LengthNumA - 1 - i] - '0';

    //倒叙插入补齐个位,并且让字符串变成可以运算的整数
    for (int i = 0; i < LengthNumB; i++)
        NumberB[i] = NumB[LengthNumB - 1 - i] - '0';

    /以上部分道理同上函数
    int LengthAns = LengthNumA + LengthNumB;
    /*
    i和j位的数字相乘会落到i+j  和  i+j+1位置上面
    数学问题,可以C一下,网上有很多这种算法
    */
    int TEMP;//临时装一下变量
    for (int i = 0; i < LengthNumA; i++)
    {//乘数
        for (int j = 0; j < LengthNumB; j++)
        {//被乘数
            TEMP = (NumberA[i] * NumberB[j]);
            TEMP += NumberAns[i + j];
            NumberAns[i + j] = TEMP % 10;//这里用倒查法,逻辑会简单一点,
            NumberAns[i + j + 1] += TEMP / 10;
        }
    }
    //然后就要把高位的0去掉
    while (!NumberAns[LengthAns - 1])
    {
        LengthAns--;
    }
    //倒查法装填字符串
    for (int i = LengthAns - 1; i >= 0; i--)//装填到字符串里面
        NumAns += NumberAns[i] + '0';
    return NumAns;

}