【更新日志】

论文信息：Off-Policy Deep Reinforcement Learning without Exploration, [Github]

本文主要介绍的是连续空间状态下的策略约束的BCQ算法， 作者首先就offline RL中容易出现extrapolation error现象进行了解释，然后用数学证明了在某些条件下这种误差是可以消除的，最后引入了BCQ算法，通过batch constrain的限制来避免这样的误差，实验证明BCQ算法的效果很好。

1 Batch RL

1.1 Online与Offline

Online与Offline的区别在于是否与环境实时交互，标准的的RL算法通过反复试错来学习如何执行任务，并在探索与利用之间进行平衡达到更好的表现，而Offline RL要求智能体从固定的数据集汇总进行学习，不能进行探索，因此Offline研究的是如何最大限度的利用静态的离线数据集来训练RL智能体。

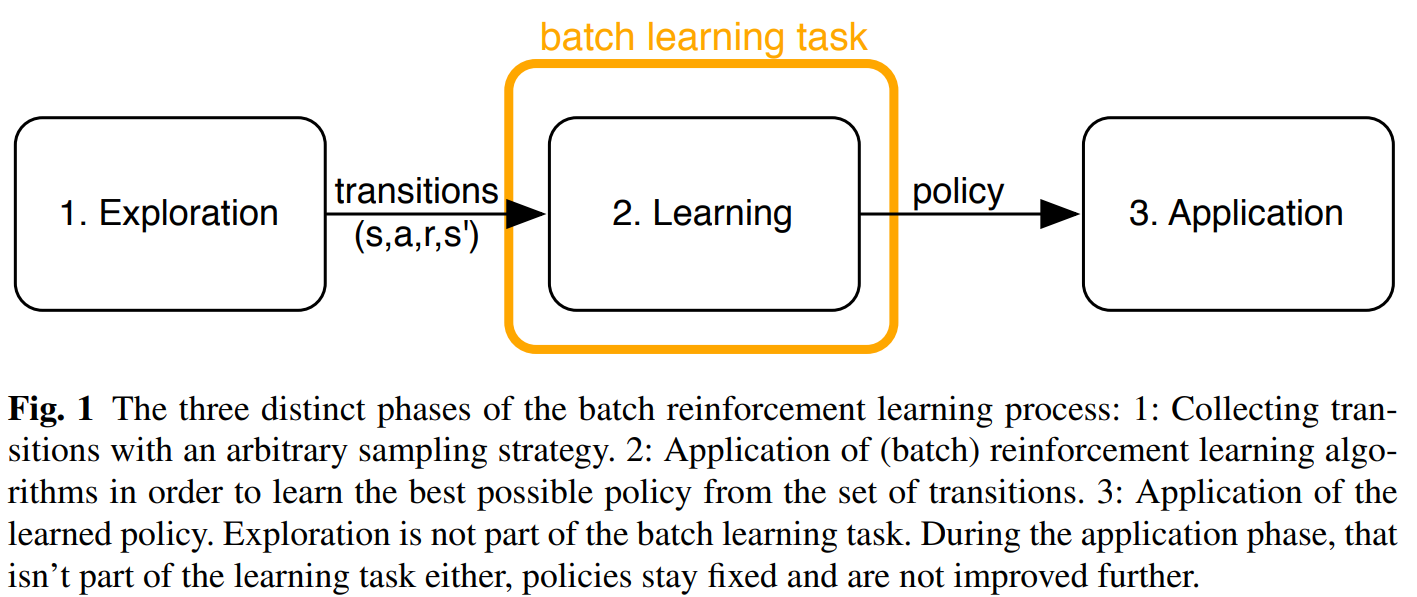
1.2 Batch RL 研究方向

1.2.1 数据集

• 离线数据集大小。谷歌训练离线 QR-DQN 和 REM 所用的数据集是通过随机下采样整个 DQN 回溯数据集得到的简化数据，同时保持了相同的数据分布。与监督学习类似，模型的性能会随着数据集大小的增加而提升。例如REM 和 QR-DQN 只用整个数据集的 10% 就达到了与完全的 DQN 接近的性能；
• 离线数据集的组成。通过使用 DQN 算法回溯多个游戏的训练数据，离线 REM 和 QR-DQN 在这个低质量数据集上的表现优于最佳策略（best policy），这表明如果数据集足够多样，标准强化学习智能体也能在离线设置下表现良好；

1.2.2 算法

策略约束

• 显示策略约束
  (类似于 TRPO): 估计行为策略 ${\pi }_{\beta }$, 并约束目标策略 ${\pi }_{\theta }$ 使其接近 于 ${\pi }_{\beta }$ 。最大化如下目标函数:
  $$J\left({\pi }_{\theta }\right)={\mathbb{E}}_{s\sim d^{\pi }\theta (s),a\sim {\pi }_{\theta }(a\mid s)}\left[Q^{\pi }(s,a)\right]$$
  $$\text{ s.t. }D\left({\pi }_{\theta }(\cdot \mid s),{\hat{\pi }}_{\beta }(\cdot \mid s)\right)\le \epsilon$$

• 隐式策略约束

  (类似于PPO): 不依赖于对行为策略 ${\pi }_{\beta }$ 的估计, 而是通过使用改进的目标函数和严格依赖 ${\pi }_{\beta }$ 的样本来隐式约束目标策略 ${\pi }_{\theta }$ ，上述显式目标函数可以转化为:
  $$\mathcal{L}(\pi ,\lambda )={\mathbb{E}}_{s\sim d^{\pi }\beta (s)}\left[{\mathbb{E}}_{a\sim \pi (a\mid s)}\left[{\hat{A}}^{\pi }(s,a)\right]+\lambda \left(\epsilon -D_{KL}\left(\pi (\cdot \mid s),{\pi }_{\beta }(\cdot \mid s)\right)\right)\right]$$

  • 对函数 $\pi$ 求偏导使之为 0 , 可以得到: ${\pi }^{\ast }(a\mid s)\propto {\pi }_{\beta }(a\mid s)\exp \left({\lambda }^{-1}{\hat{A}}^{{\pi }_k}(s,a)\right)$
    
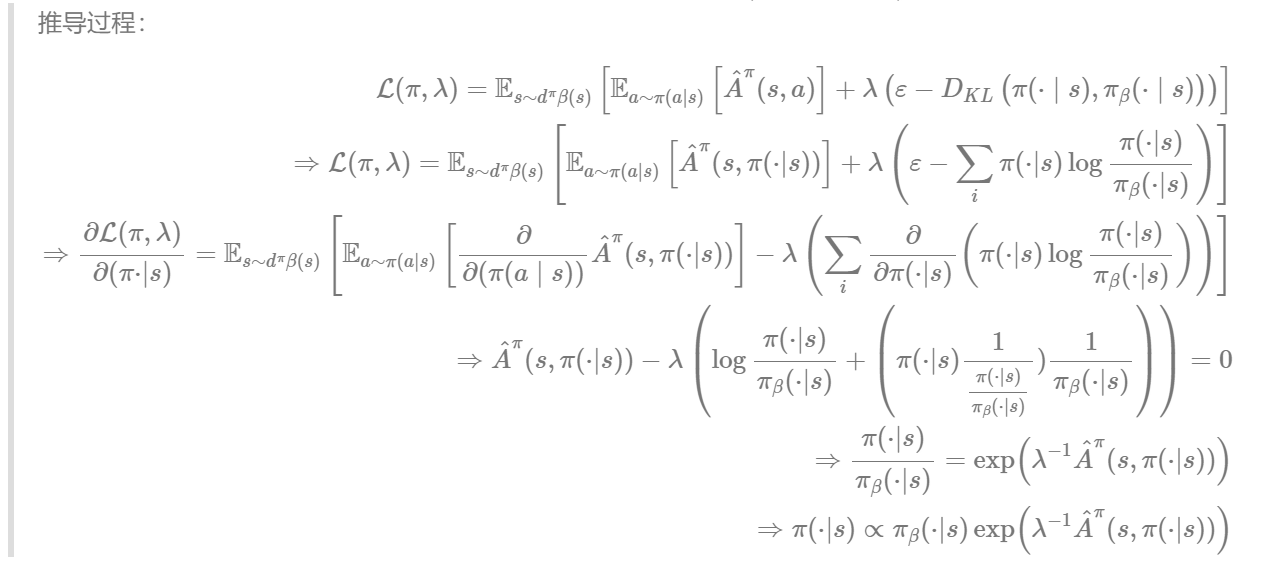
  • 因此, 隐式目标函数改进为: (这里参见Advantage-Weighted Regression (AWR))
    $$\underset{{\pi }_{\theta }}{\mathrm{argmin}}{\mathbb{E}}_{s\sim \mathcal{D}}\left[D_{KL}\left({\pi }^{\ast }(\cdot \mid s),{\pi }_{\theta }(\cdot \mid s)\right)\right]=\underset{{\pi }_{\theta }}{\mathrm{argmax}}{\mathbb{E}}_{s,a\sim \mathcal{D}}\left[\log {\pi }_{\theta }(a\mid s)\exp \left({\lambda }^{-1}{\hat{A}}^{\pi }(s,a)\right)\right]$$

2 Extrapolation Error

错误的估计了状态动作值，本质上是经验池中的数据分布和当前策略的数据分布不一致，产生了分布偏移的情况。模型在一个分布下训练，但是在不同的分布下评估，如果经验池中缺少状态动作的样本，那么也就不可能学到策略。

2.1 Absent Data

某些$state-action$对在数据集中不存在，那么这个动作的$Q$值就无法更新。

2.2 Model Bias

模型自身存在的偏差，当我们用数据集$\mathcal{B}$训练模型时，$Bellman$算子$(operator)$其实是通过从$\mathcal{B}$中采样轨迹$(s,a,r,s^{\prime })$来估计的，即

$${\mathcal{T}}^{\pi }Q(s,a)\approx {\mathbb{E}}_{s^{\prime }\sim \mathcal{B}}\left[r+\gamma Q\left(s^{\prime },\pi \left(s^{\prime }\right)\right)\right]$$

数据集$\mathcal{B}$的大小有限，$state-action$的访问次数也是有限的，那么数据的分布就会产生偏差，关于$s^{\prime }$的期望就会有$bias$，因为在$\mathcal{B}$中采样$s^{\prime }$很难逼近真实MDP中$s^{\prime }$的分布。

2.3 Training Mismatch

当数据集$\mathcal{B}$中的数据量充足的时候，模型可以进行均匀采样，损失函数的权重是和轨迹似然相关的，于是损失函数是

$$\approx \frac{1}{|\mathcal{B}|}\sum _{\left(s,a,r,s^{\prime }\right)\in \mathcal{B}}{\Vert r+\gamma Q_{{\theta }^{\prime }}\left(s^{\prime },\pi \left(s^{\prime }\right)\right)-Q_{\theta }(s,a)\Vert }^2$$

当数据集中的数据分布和当前策略下的数据分布不一致的时候，$Q$函数对于当前策略选出的动作的值估计是很差的，因为此时均匀的权重$\frac{1}{|\mathcal{B}|}$不再匹配当前策略下真实的权重。
而且当前策略下有高似然的$state-action$对可能无法在数据集中找到，这样也会有误差。

2.4 实验验证

2.4.1 Final buffer

从头训练一个DDPG算法，运行100万步（加入了高斯噪声来保证充分探索）并将遇到的轨迹全部储存在经验池，保证充分覆盖到所有的轨迹。

2.4.2 Concurrent

在Final buffer设置的基础上同时训练一个off-policy的智能体，并行训练100万步，俩个都用behavioral DDPG agent采样得到的经验池中的数据进行训练。

2.4.3 Imitation

使用一个训练好的DDPG从环境中采集100万步数据，没有探索。

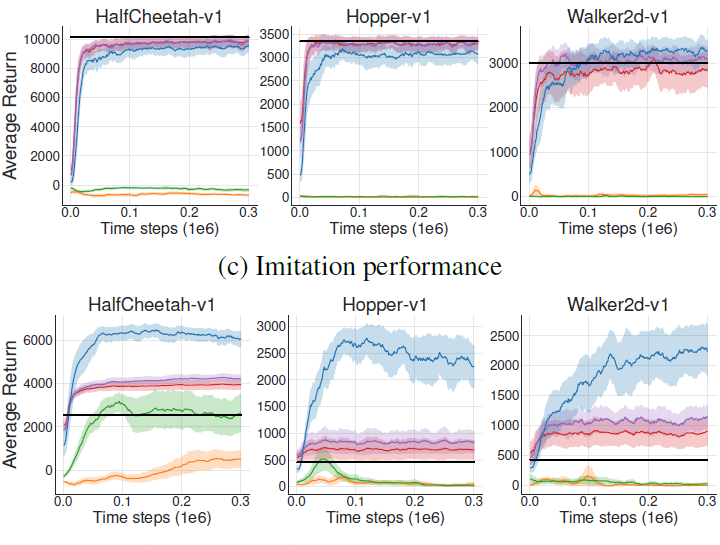
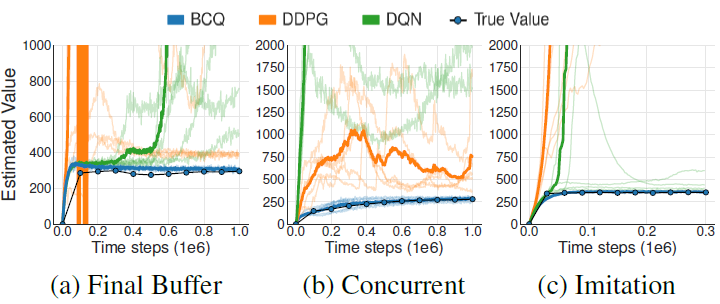
结果如图所示，其中True Value是用Monte Carlo算出来的。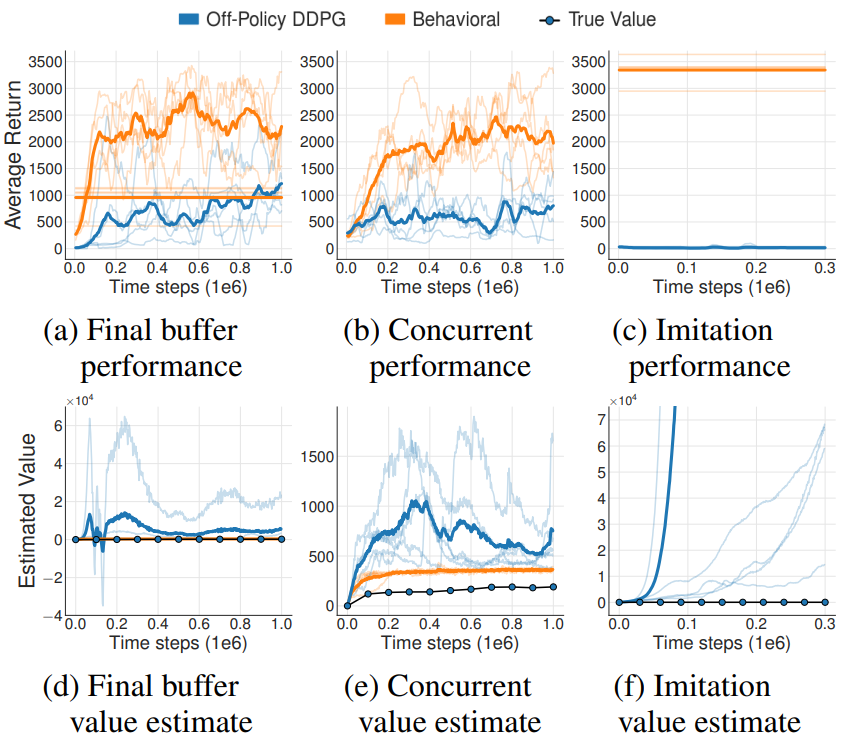

从图中可以看出，off-policy的DDPG的结果很差，即便和behavioral DDPG agent同时训练，也有很大的差距，这说明在稳定的状态分布下，初始策略的差异便可导致Extrapolation Error。而在imitation中，数据集中都是专家数据，在评估非专家的动作时，就会出现value的过估计问题。

on-line设置下，推断误差会导致过分估计，推测误差通过隐式的“乐观面对不确定性”策略可能促使有用的探索其值估计会慢慢修正。但是off-line是基于batch的，不能和环境进行交互，这样的误差将很难被消除。

3 策略约束

通过限制策略选择的$state-action$对和$batch$中的存在的数据相似，那么动作的值估计就会变得准确了。

3.1策略选择的目标

• 最小化所选择的动作和数据集中存在的工作的距离
• 能转移到和数据集中状态相似的状态
• 最大化值函数

第一点最重要，通过限制所选择的动作，来增加值估计的准确性。增加了一个生成网络来限制动作之间的距离，再加上Q网络来选择最高价值的动作。为了评估相似状态，在价值更新时利用两个Q网络的估计再取soft minimum。

3.2 处理推测误差

Q值更新公式：
$$Q(s,a)\leftarrow (1-\alpha )Q(s,a)+\alpha \left(r+\gamma Q\left(s^{\prime },\pi \left(s^{\prime }\right)\right)\right)$$
其中$\pi \left(s^{\prime }\right)={\mathrm{argmax}}_{a^{\prime }}Q\left(s^{\prime },a^{\prime }\right)$，从数据集 $\mathcal{B}$ 学习的 $\mathrm{Q}$ 函数，定义一个对应的 $MDP$ 为 $M_{\mathcal{B}}$，真实的 $MDP$ 记为 $M$。$M_{\mathcal{B}}$ 和 $M$ 具有相同的动作空间和状态空间，初始状态为$s_{init}$，初始动作值是$Q(s,a)$，$M_{\mathcal{B}}$的状态转移概率是$p_{\mathcal{B}}\left(s^{\prime }\mid s,a\right)=\frac{N\left(s,a,s^{\prime }\right)}{{\sum }_{\tilde{s}N(s,a,s)}}$ ，其中 $N\left(s,a,s^{\prime }\right)$ 表示在数据集 $\mathcal{B}$ 遇见 $N\left(s,a,s^{\prime }\right)$ 的数量。如果 ${\sum }_{\tilde{s}}N(s,a,\tilde{s})=0$ ，则 $p_{\mathcal{B}}\left(s_{init}\mid s,a\right)=1$ ，并且 $r\left(s,a,s_{init}\right)$ 被设置为 $Q(s,a)$ 的初始值。

3.2.2 定理1

从数据集$\mathcal{B}$中采样进行 $Q-learning$ 学习，在 $MDP$ $M_{\mathcal{B}}$中，$Q-learning$ 最终会收敛到最优动作值函数。

${ϵ}_{\mathrm{M}\mathrm{D}\mathrm{P}}$是有限MDP下的推测误差，也就是两个Q值的差：
$${ϵ}_{\mathrm{M}\mathrm{D}\mathrm{P}}(s,a)=Q^{\pi }(s,a)-Q_{\mathcal{B}}^{\pi }(s,a)$$

转换成贝尔方程的形式是：
$$\begin{array}{rl}{ϵ}_{\mathrm{M}\mathrm{D}\mathrm{P}}(s,a)=& \sum _{s^{\prime }}\left(p_M\left(s^{\prime }\mid s,a\right)-p_{\mathcal{B}}\left(s^{\prime }\mid s,a\right)\right)\\ & \left(r\left(s,a,s^{\prime }\right)+\gamma \sum _{a^{\prime }}\pi \left(a^{\prime }\mid s^{\prime }\right)Q_{\mathcal{B}}^{\pi }\left(s^{\prime },a^{\prime }\right)\right)\\ & +p_M\left(s^{\prime }\mid s,a\right)\gamma \sum _{a^{\prime }}\pi \left(a^{\prime }\mid s^{\prime }\right){ϵ}_{\mathrm{M}\mathrm{D}\mathrm{P}}\left(s^{\prime },a^{\prime }\right)\end{array}$$

这意味推断误差可以视为转移概率的差值的函数，其中动作值视为权重。如果选择一个策略使得两个转移概率的差距最小，那么推断误差也能达到最小。

$${ϵ}_{\mathrm{M}\mathrm{D}\mathrm{P}}^{\pi }=\sum _s{\mu }_{\pi }(s)\sum _a\pi (a\mid s)\left|{ϵ}_{\mathrm{M}\mathrm{D}\mathrm{P}}(s,a)\right|$$

3.2.2 定理2

对于确定性的 MDP 和任意的奖励函数，当且仅当策略 $\pi$ 是batch-constrained时，${ϵ}_{\mathrm{M}\mathrm{D}\mathrm{P}}$=0 。另外，如果数据集 $\mathcal{B}$ 是连贯的，那么这样的策略一定存在，初始状态$s_0\in \mathcal{B}$ 。

$$Q(s,a)\leftarrow (1-\alpha )Q(s,a)+\alpha \left(r+\gamma \underset{a^{\prime }\text{ s.t. }\left(s^{\prime },a^{\prime }\right)\in \mathcal{B}}{\max }Q\left(s^{\prime },a^{\prime }\right)\right)$$

3.2.3 定理3

学习率为 $\alpha$，通过对环境标准的采样，BCQL 可以收敛到最优动作值函数 $Q^{\ast }$ 。

3.2.4 定理4

给定确定性 MDP 和 coherent 数据集 $\mathcal{B}$ ，学习率为 $\alpha$，BCQL 将会收敛到 $Q_{\mathcal{B}}^{\pi }(s,a)$ ，其中 ${\pi }^{\ast }(s)=\arg {\max }_{a\text{ s.t. }(s,a)\in \mathcal{B}}{Q}_{\mathcal{B}}^{\pi }(s,a)$ 是最优 batch-constrained 策略。

3.3 BCQ算法

将 BCQL 算法拓展到连续环境，本文提出了 BCQ 算法。其中为了满足 Batch-constrained 的条件，BCQ 利用了一个生成模型。对于给定的状态，BCQ 利用生成模型来生成与 batch 相似的动作集合，并通过 Q 网络来选择价值最高的动作。另外，还对价值估计过程增加了对未来稀有的状态进行惩罚，与 Clipped Double Q-learning 算法类似。最后，BCQ 能学到与数据集的状态动作对访问分布相似的策略。

给定状态 $s$ ，将 $(s,a)$ 和数据集 $\mathcal{B}$ 中的状态动作对的相似度建模成条件概率 $P_{\mathcal{B}}^G(a\mid s)$ 。为了估计 $P_{\mathcal{B}}^G(a\mid s)$ ，采用参数化的生成模型 $G_{\omega }(s)$ ，从中采样动作来逼近 $\arg {\max }_a{P}_{\mathcal{B}}^G(a\mid s)$ 。
使用变分自动编码器 $VAE$ 来提高生成动作的多样性，引入扰动模型 ${\xi }_{\varphi }(s,a,\Phi )$ ，对动作 $a$ 的扰动范围是 $[-\Phi ,\Phi ]$ 。此时策略可 以表示为：

$$\pi (s)=\arg \underset{a_i+{\xi }_{\varphi }\left(s,a_i,\Phi \right)}{\max }{Q}_{\theta }\left(s,a_i+{\xi }_{\varphi }\left(s,a_i,\Phi \right)\right),{\left\{a_i\sim G_{\omega }(s)\right\}}_{i=1}^n$$

参数 $n$ 和 $\Phi$ 的选择让 BCQ 算法介于模仿学习和强化学习之间。当 $\Phi =0$ 且 $n=1$ 时，BCQ 就类似于模仿学习；当 $\Phi =a_{\max }-a_{\min }$ 且 $n\to \infty$ 时，BCQ 算法就类似于 Q-learning 算法。
扰动模型 ${\xi }_{\varphi }$ 的训练和 DDPG 算法的训练目标类似:

$$\varphi \leftarrow \underset{\varphi }{\mathrm{argmax}}\sum _{(s,a)\in \mathcal{B}}{Q}_{\theta }\left(s,a+{\xi }_{\varphi }(s,a,\Phi )\right)$$

为了对末来一些不常见的状态进行惩罚，采用 Clipped Double Q-learning 算法 对动作值 $Q$ 进行估计，也就是训练两个动作值网络 $\left\{Q_{{\theta }_1},Q_{{\theta }_2}\right\}$ ，取它们的最小值作为动作值的估计。改进 Clipped Double Q-learning 算法，对两个动作值采用新的结合方式:

$$y=r+\gamma \underset{a_i}{\max }\left[\lambda \underset{j=1,2}{\min }{Q}_{{\theta }_j^{\prime }}\left(s^{\prime },a_i\right)+(1-\lambda )\underset{j=1,2}{\max }{Q}_{{\theta }_j^{\prime }}\left(s^{\prime },a_i\right)\right]$$

class BCQ(object):
	def __init__(self, state_dim, action_dim, max_action, device, discount=0.99, tau=0.005, lmbda=0.75, phi=0.05):
		latent_dim = action_dim * 2

		self.actor = Actor(state_dim, action_dim, max_action, phi).to(device)
		self.actor_target = copy.deepcopy(self.actor)
		self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=1e-3)

		self.critic = Critic(state_dim, action_dim).to(device)
		self.critic_target = copy.deepcopy(self.critic)
		self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=1e-3)

		self.vae = VAE(state_dim, action_dim, latent_dim, max_action, device).to(device)
		self.vae_optimizer = torch.optim.Adam(self.vae.parameters()) 

		self.max_action = max_action
		self.action_dim = action_dim
		self.discount = discount
		self.tau = tau
		self.lmbda = lmbda
		self.device = device


	def select_action(self, state):		
		with torch.no_grad():
			state = torch.FloatTensor(state.reshape(1, -1)).repeat(100, 1).to(self.device)
			action = self.actor(state, self.vae.decode(state))
			q1 = self.critic.q1(state, action)
			ind = q1.argmax(0)
		return action[ind].cpu().data.numpy().flatten()


	def train(self, replay_buffer, iterations, batch_size=100):

		for it in range(iterations):
			# Sample replay buffer / batch
			state, action, next_state, reward, not_done = replay_buffer.sample(batch_size)

			# Variational Auto-Encoder Training
			recon, mean, std = self.vae(state, action)
			recon_loss = F.mse_loss(recon, action)
			KL_loss	= -0.5 * (1 + torch.log(std.pow(2)) - mean.pow(2) - std.pow(2)).mean()
			vae_loss = recon_loss + 0.5 * KL_loss

			self.vae_optimizer.zero_grad()
			vae_loss.backward()
			self.vae_optimizer.step()


			# Critic Training
			with torch.no_grad():
				# Duplicate next state 10 times
				next_state = torch.repeat_interleave(next_state, 10, 0)

				# Compute value of perturbed actions sampled from the VAE
				target_Q1, target_Q2 = self.critic_target(next_state, self.actor_target(next_state, self.vae.decode(next_state)))

				# Soft Clipped Double Q-learning 
				target_Q = self.lmbda * torch.min(target_Q1, target_Q2) + (1. - self.lmbda) * torch.max(target_Q1, target_Q2)
				# Take max over each action sampled from the VAE
				target_Q = target_Q.reshape(batch_size, -1).max(1)[0].reshape(-1, 1)

				target_Q = reward + not_done * self.discount * target_Q

			current_Q1, current_Q2 = self.critic(state, action)
			critic_loss = F.mse_loss(current_Q1, target_Q) + F.mse_loss(current_Q2, target_Q)

			self.critic_optimizer.zero_grad()
			critic_loss.backward()
			self.critic_optimizer.step()


			# Pertubation Model / Action Training
			sampled_actions = self.vae.decode(state)
			perturbed_actions = self.actor(state, sampled_actions)

			# Update through DPG
			actor_loss = -self.critic.q1(state, perturbed_actions).mean()
		 	 
			self.actor_optimizer.zero_grad()
			actor_loss.backward()
			self.actor_optimizer.step()


			# Update Target Networks 
			for param, target_param in zip(self.critic.parameters(), self.critic_target.parameters()):
				target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)

			for param, target_param in zip(self.actor.parameters(), self.actor_target.parameters()):
				target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)

4 实验结果

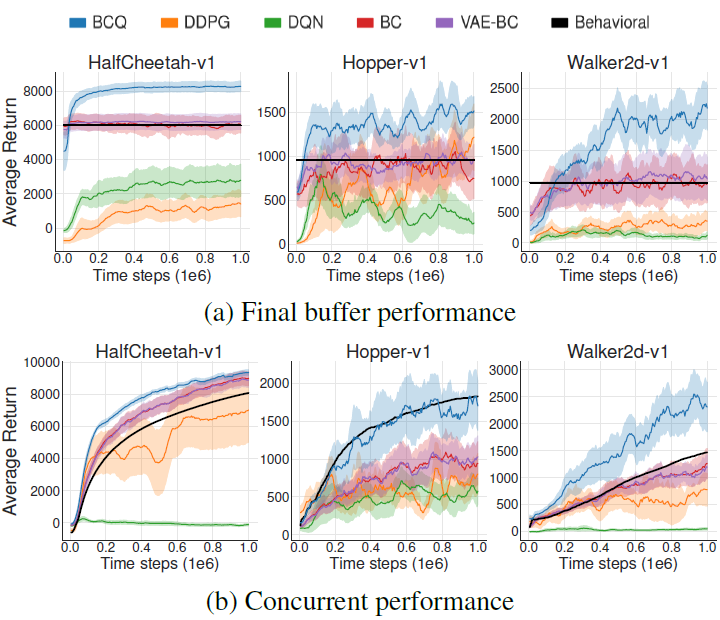
如下图所示，BCQ的值估计准确而且稳定，这说明推测误差得到了很好的解决。BCQ可以从不好的数据示例中进行学习，并可以超过示例，此外，相较于一般的DRL算法，BCQ需要的迭代次数很少。

参考文献

[1]. John Schulman, Sergey Levine, Philipp Moritz, Michael I. Jordan, Pieter Abbeel: “Trust Region Policy Optimization”, 2015; arXiv:1502.05477.
[2]. Scott Fujimoto, David Meger, Doina Precup: “Off-Policy Deep Reinforcement Learning without Exploration”, 2018; arXiv:1812.02900.
[3]. Scott Fujimoto, Edoardo Conti, Mohammad Ghavamzadeh, Joelle Pineau: “Benchmarking Batch Deep Reinforcement Learning Algorithms”, 2019; arXiv:1910.01708.
[4].batch constrained deep Q-learning- 张楚珩,2020
[5]. 离线强化学习(A Survey on Offline Reinforcement Learning)
[6]. Batch RL与BCQ算法