C/C++中位运算杂谈

一、位运算

1、基本操作

计算机中所有数据最终的存储形式均是二进制码。相信很多朋友和我一样，在大学中的课程中，很多课程前几章都会学习关于进制、原码、补码等东西。其实位运算是非常有用的。首要的一点，效率。位运算效率是非常高的，以及位运算肯定是非常节约空间的。

记得以前拜读过程明明老师的一篇论文， BING: Binarized Normed Gradients for Objectness Estimation at 300fp, Ming-Ming Cheng, Ziming Zhang, Wen-Yan Lin, Philip H. S. Torr, IEEE International Conference on Computer Vision and Pattern Recognition (IEEE CVPR), 2014. (Oral, Accept rate: 5.75%)。其中很有趣的一部分就是将算法进行二进制近似然后转化为二进制操作，也是整个论文中极为精彩的部分。程明明老师给出的源码运行速度很快！曾经尝试过将代码输入改为摄像头图像输入，完全能够达到实时的标准。

在C/C++中，提供了基本的一些位运算。例如 &（与）、 | （或）、~（非）、^（异或）、<<（左移）以及>>（右移）。

其中异或操作，可以理解为 “ 相同则为假，不同则为真。”同或无非是异或的反。

    // 0xAB = 0b 1010 1011
    char bitA = 0xAB;
    // ~0xAB = ~(0b 1010 1011) = 0b 0101 0100 = 0x54
    char bitB = ~bitA;
    // 右移操作, 右边以 0 进行填充
    // 0xAB << 2 = 0b 1010 1011 << 2 = 0b 1010 1100 = 0xAC
    char bitC = bitA << 2;
    // 0x54 & 0xAC = 0b 0101 0100 & 0b 1010 1100 = 0b 0000 0100 = 0x04
    char bitD = bitB & bitC;
    // 左移操作, 如是对有符号数进行操作, 则以 1 填充
    // 0xAB >> 5 = 0b 1010 1011 >> 5 = 0b 1111 1101 = 0xFD
    char bitE = bitA >> 5;
    unsigned char bitF = 0xFF;   // 0x05 = 0b 0000 0101
    // 左移操作, 如是对无符号数进行操作, 则以 1 填充
    // 0xFF >> 5 = 0b 1111 1111 >> 5 = 0b 0000 0111 = 0x07
    bitF = bitF >> 5; // 此处有另一种写法, bitF >>= 5.
    // 0xAB ^ 0xFD = 0b 1010 1011 ^ 0b 1111 1101 = 0b 0101 0110 = 0x56
    char bitG = bitA ^ bitE;
    // 0xAB | 0x04 = 0b 1010 1111 = 0xAF
    char bitH = bitA | bitD;

由上诉代码可以直观的看到每一种操作的执行.与、或、非、异或等操作均是按位操作，将前后操作数的对应位进行相应操作。

另，上诉代码测试与Win7 + VS2010。下述代码也一样。

2、组合操作

2.1 大小端模式

很多朋友应该接触过大小端模式.两种不同的存储数据方式.

大端模式，是指数据的高字节保存在内存的低地址中，而数据的低字节保存在内存的高地址中，这样的存储模式有点儿类似于把数据当作字符串顺序处理：地址由小向大增加，而数据从高位往低位放；

小端模式，是指数据的高字节保存在内存的高地址中，而数据的低字节保存在内存的低地址中，这种存储模式将地址的高低和数据位权有效地结合起来，高地址部分权值高，低地址部分权值低，和我们的逻辑方法一致。

一般的, 我们可以使用联合体来判断自己计算机是采用什么样的存储模式.代码如下:

union mode_test {  
    unsigned int  i;  
    unsigned char c;
};

union mode_test1 {  
    unsigned short  i;  
    unsigned char   c;
};

int _tmain(int argc, _TCHAR* argv[]) {
    union mode_test1 mt1; // 仅仅为了显示结构体占用字节数的方式
    union mode_test mt;
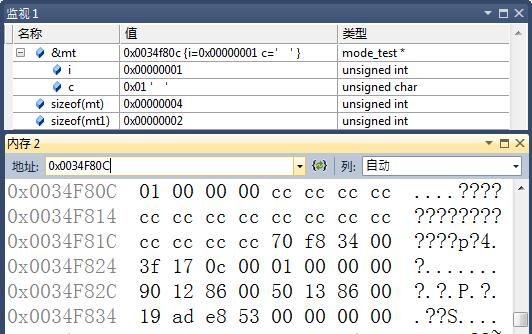
    mt.i = 1;
    if (0x01 == mt.c) {
        printf("小端模式\n");
    } else {
        printf("大端模式\n");
    }
}

因为联合体的缘故, mode_test中c和i均是存在同一内存中.如果c(占用一个字节)的值是0x01的话, 那么说明该计算机的存储方式是将低字节数据存放在低地址中.或者相反.这样就可以判断该计算机是属于哪一种存储方式了.程序调试截图如下:

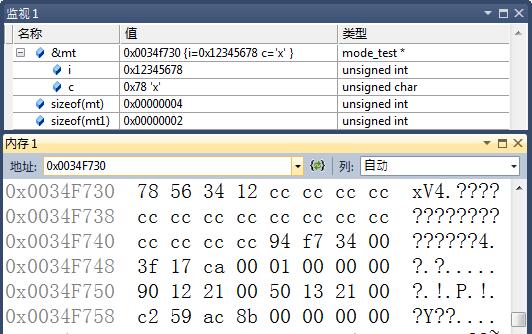
这里写图片描述

由上图可以看到, 其中0x01数据是存放在低地址段.而高位数据存放在高地址中.同样, c是等于0x01.另, 图中也可以看出, 联合体占用的字节数和其中数据类型有关系.

mt.i = 0x12345678;

这里写图片描述

2.2 结构体的位域

在代码中，很多朋友可能会和我有一样的经历。就是想设定一个变量记录某个范围，这个范围是确定的，假如是 [0, 111], 很显然, 一个int 搓搓有余.但是如果内存有限, 就会感觉很浪费.这个时候用一个unsigned char就会更好一些.

同样的问题也会出现在一些标志位. 只是需要两个值来代表真假即可.这个时候可以选用bool, 但是bool是占用一个字节的.如果标志位很多, 也会存在浪费的问题.

其实在C/C++中结构体是可以使用位域的,定义精确到每个成员占用几个bit.定义如下:

struct bit_struct_name1 {
    char a:8;
    char b:2;
    char c:5;
};

struct bit_struct_name2 {
    int a:30;
    int b:4;
    int c:5;
};

int _tmain(int argc, _TCHAR* argv[]) {
    struct bit_struct_name1 s1;
    s1.a = 20; // 0b 0001 0100
    s1.b = 3;  // 0b 11
    s1.c = 2;  // 0b 0 0010
    struct bit_struct_name2 s2;
    s2.a = 20; // 0b 0001 0100
    s2.b = 3;  // 0b 0011
    s2.c = 2;  // 0b 0 0010
}

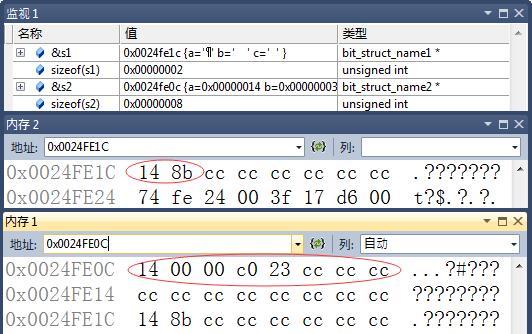
调试后截图如下:

这里写图片描述

从上图中可以看到两个结构体具体的内存分布以及对齐方式.

第一个结构体占用两个字节.可以看到, 结构体1的数据类型均是char, 所以最小存储单位是1个字节(char占用一个字节). 结构体2的数据类型均是int, 所以最小存储单位是4个字节,(int占用4个字节).

从图中可以看到, 结构体1占用2个字节, 结构体2占用8个字节.再看一看其中内存中是如何存储的.

结构体1,占用2个字节:
数据:
0x14 8b = 0b 0001 0100 1000 1011
在代码中, 我们赋值分别:
a = 20(0b 0001 0100); // 8bit
b = 3(0b 11); // 2bit
c = 2(0b 10). // 5bit
由前面讨论的可以知道, 我电脑是将高字节数据存放在高地址的. 而s1.b和s1.c是存放在同一个字节中的, 所以最后两位是0b11, 接着是0b01 000五个字节.最后填充了一个1. 构成了第二字节内存. 0b 1000 1011.其中填充的值到底是1还是0, 不同系统不同编译器是有不同定义的.编码的过程中也不应该假定填充位是什么.这样是不合理的.

结构体2, 占用8个字节,
数据:
0x14 00 00 c0 23 cc cc cc = 0b 0001 0100 0000 0000 0000 0000 1100 0000 0010 0011 1100 1100 1100 1100 1100 1100,
代码中, 赋值内容分别是:
a = 20(0b 0001 0100); // 30bit
b = 3(0b 11); // 4bit
c = 2(0b 10). // 5bit
其中, a占用30bit, 一个int占用4字节,即32bit, 而第二个数据b,占用4个字节, 第一个4字节不够用了,故a单独占用第一个4字节,内容是0b 0001 0100 0000 0000 0000 0000 xx00 0000,并且需要扩展一个单位内存用于存放剩下的数据, 这个单位内存的大小由最大sizeof值决定, 该例中是int占用4个字节最大,故以4字节对齐.则b被放到第二个4字节中.b需要4个bit, 紧接着是c需要5个bit. 则a和b被存放在两个字节中, 并且高字节数据存放在高地址中, 高地址应该由a和b共同组成, a构成其中的低4个bit, b贡献高4个bit.则第5个字节数据应该是: 0010 0011, 第6个字节的最末位是b的最高位0.

由上分析可知, 其中内存分布应该是:

0b 0001 0100 0000 0000 0000 0000 xx00 0000 0010 0011 xxxx xxx0 xxxx xxxx xxxx xxxx

其中x均是填充位.对比实际内存数据, 可以看到, 填充位有些是0 有些是1.下面我们变更一下数据验证我们的想法.如果a占用31个bit, c的最高位是1, 即c的五个bit: 1 0010.那么理论内存数据是:

0b 0001 0100 0000 0000 0000 0000 x000 0000 0010 0011 xxxx xxx1 xxxx xxxx xxxx xxxx

测试代码如下:

struct bit_struct_name2 s2;
s2.a = 20; // 0b 0001 0100, 31bit
s2.b = 3;  // 0b 0011, 4bit
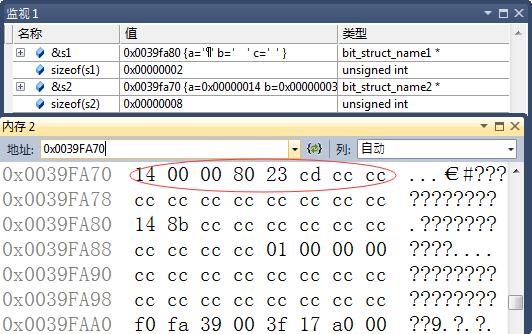
s2.c = 18;  // 0b 1 0010, 5bit

调试截图如下:

这里写图片描述

由上可以看到, 内存实际数据:

0x 14 00 00 80 23 cd cc cc = 0b 0001 0100 0000 0000 0000 0000 1000 0000 0010 0011 1100 1101 1100 1100

其中, a占用31bit, 前4个字节理论值:0001 0100 0000 0000 0000 0000 x000
b占用4bit. c占用5bit. 则第5个字节理论值: 0010 0011
第6个字节理论值: xxxx xxx1.其他字节均是xxxx xxxx上诉调试值正好验证我们的想法.

三、简单运用

3.1 求某个字段内1的个数

给定一个int, 计算出int的二进制表示中共有多少个1. 例如int a = 254; // 0b 0000 0000 0000 0000 0000 0000 1111 1110中共有7个1.

代码实现如下:

unsigned int countOne(unsigned int n) {
    unsigned int count = 0;
    while (0 != n) {
        n &= (n -1); // n = n & (n - 1)
        ++count;
    }
    return count;
}

其中的关键在于n &= (n -1), 该位运算完成一个作用, 消去n的二进制表示中的一个1.如果, n=0b 1110 1010, 则n-1=0b 1110 1001, n & (n - 1)=0b 1110 1000,如果n=0b 1110 1011, 则n-1=0b 1110 1010, n & (n - 1)=0b 1110 1010.

3.2 向上对齐

在STL源代码中, 有一段代码给我印象特别深,其中也是用到了位运算.在空间配置的问题上,为了避免内存碎片,所以在申请小于128 byte内存时, 假设申请x大小内存, STL会上调x值至大于等x的最小8的倍数.例如,申请4个字节,则上调至8,申请25个字节,则上调至32,依次类推.

实现上诉功能的STL源码如下所示:

enum {_ALIGN = 8};
static size_t  _S_round_up(size_t __bytes) 
    { return (((__bytes) + (size_t) _ALIGN - 1) & ~((size_t) _ALIGN - 1)); }

如上所示, 函数很简洁, 一句话完成上诉功能.可以将这句话拆分为两部分, A = ((__bytes) + (size_t) _ALIGN - 1), B = ~((size_t) _ALIGN - 1).最终的结果是A & B.

假设,申请内存大小__bytes是属于 $((n - 1) \cdot 8, n \cdot 8]$ 范围内, 则目标大小应该是 $n \cdot 8$ .

A 完成将申请内存大小__bytes增大到 $[n \cdot 8, (n - 1) \cdot 8 )$ .

B 的作用是类似于得到一个算子. $8 - 1 = 7$ , 而 $7$ 对应的二进制是末三位为1, 其余位是0.取反后,则得到末三位是0, 其余位是1.

A & B, 则表示将A的末三位置零, 其余位保留.就得到目标值 $n \cdot 8$ .

8的倍数,即能够整除8.除8又可以转换为位运算,即右移三位.整除8,即除数的末三位都是0,右移后没有任何数据丢失.

3.3 不声明额外变量完成变量交换

在我印象中, 在大学中学习C/C++时, 冒泡排序中提供了一个经典的变量交换代码实现.类似如下:

void swap(int& a, int& b) {
    int tmp = a;
    a = b;
    b = tmp;
}

但是不声明额外的变量, 可以用如下方式:

void swap(int& a, int& b) {
    a += b; // a = a + b;
    b = a - b;
    a = a - b;
}

也可以使用位运算:

void swap(int& a, int& b) {
    a ^= b; // a = a ^ b;
    b = a ^ b;
    a = a ^ b;
}

其中, 另a和b分别是逻辑变量A,B, 则第一句

A = (A ¯ ¯ ¯ \cap B) \cup (A \cap B ¯ ¯ ¯)

$A = (\overline {A} \cap B) \cup ( A \cap \overline{B})$
第二句:

B = ((A ¯ ¯ ¯ \cap B) \cup (A \cap B ¯ ¯ ¯) ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ \cap B) \cup ((A ¯ ¯ ¯ \cap B) \cup (A \cap B ¯ ¯ ¯) \cap B ¯ ¯ ¯)

$B = (\overline {(\overline {A} \cap B) \cup ( A \cap \overline{B})} \cap B) \cup ( (\overline {A} \cap B) \cup ( A \cap \overline{B}) \cap \overline{B})$

= ((A ¯ ¯ ¯ \cap B \cup B ¯ ¯ ¯) \cup (A \cap B ¯ ¯ ¯ \cup B ¯ ¯ ¯) ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯) \cup ((A ¯ ¯ ¯ \cap B \cap B ¯ ¯ ¯) \cup (A \cap B ¯ ¯ ¯ \cap B ¯ ¯ ¯))

$= (\overline {(\overline {A} \cap B \cup \overline{B}) \cup ( A \cap \overline{B} \cup \overline{B})}) \cup ( (\overline {A} \cap B \cap \overline{B}) \cup ( A \cap \overline{B} \cap \overline{B}))$

= (A ¯ ¯ ¯ \cup (A \cap B ¯ ¯ ¯) ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯) \cup (A \cap B ¯ ¯ ¯) = B ¯ ¯ ¯ ¯ ¯ ¯ \cup A \cap B ¯ ¯ ¯ = A

$= (\overline {\overline {A} \cup (A \cap \overline{B})}) \cup ( A \cap \overline{B}) = \overline {\overline{B}} \cup A \cap \overline{B} = A$
第三句类似, 我就不推导了.

3.4 Reverse Bits

leetcode原题: Reverse bits of a given 32 bits unsigned integer.

For example, given input 43261596 (represented in binary as 00000010100101000001111010011100), return 964176192 (represented in binary as 00111001011110000010100101000000).

Follow up:
If this function is called many times, how would you optimize it?

原题链接: https://leetcode.com/problems/reverse-bits/

最简单粗暴的办法, 就是直接将对应位置的bit进行交换.

代码实现如下:

uint32_t reverseBits(uint32_t n) {
    uint32_t HIG_1 = 0x80000000;
    uint32_t LOW_1 = 0x00000001;
    uint32_t tmp = 0;
    bool isEquelHi = false;
    bool isEquelLo = false;
    for (int i = 0; i < 16; ++i) {
        tmp = n & HIG_1;
        isEquelHi = (HIG_1 == tmp);
        isEquelLo = (LOW_1 == (n & LOW_1));
        if ((isEquelHi || isEquelLo)
            && (!isEquelHi || !isEquelLo)) {
            if (tmp == HIG_1) {
                n &= ~HIG_1;
                n |= LOW_1;
            } else {
                n |= HIG_1;
                n &= ~LOW_1;
            }
       }
        HIG_1 >>= 1;
        LOW_1 <<= 1;
    }

    return n;
}

代码中对相同bit进行了简单判断, 相同则不交换, 故让代码复杂了一些.也可以不判断,直接进行交换.

uint32_t swapBits(uint32_t n, uint32_t step_lo, uint32_t step_hi) {
    const uint32_t LO_1 = 0x00000001;
    uint32_t lo = ((n >> step_lo) & LO_1);
    uint32_t hi = ((n >> step_hi) & LO_1);
    if (lo ^ hi) {
      n ^= ((LO_1 << step_lo) | (LO_1 << step_hi));
    }
    return n;
}

uint32_t reverseBits(uint32_t n) {
    const uint32_t SIZE = sizeof(n) * 8;
    for (uint32_t i = 0; i < SIZE / 2; ++i) {
      n = swapBits(n, i, SIZE-i-1);
    }
    return n;
}

还有最后一种最快的方法

uint32_t reverseBits(uint32_t n) {
    n = ((n & 0x55555555) << 1) | ((n & 0xAAAAAAAA) >> 1);
    n = ((n & 0x33333333) << 2) | ((n & 0xCCCCCCCC) >> 2);
    n = ((n & 0x0F0F0F0F) << 4) | ((n & 0xF0F0F0F0) >> 4);
    n = ((n & 0x00FF00FF) << 8) | ((n & 0xFF00FF00) >> 8);
    n = ((n & 0x0000FFFF) << 16) | ((n & 0xFFFF0000) >> 16);
    return n;
}

代码解析:
line 1: ‘n = ((n & 0x55555555) << 1) | ((n & 0xAAAAAAAA) >> 1);’

Hex	Bin
0x55555555	0b 0101 0101 0101 0101 0101 0101 0101 0101
0xAAAAAAAA	0b 1010 1010 1010 1010 1010 1010 1010 1010

n & 0x55555555, 即是将n的二进制表示中的偶数的位提取出来,奇数位全部置零;再左移一位;
n & 0xAAAAAAAA, 即是将n的二进制表示中的奇数的位提取出来,偶数位全部置零;再右移一位

即得到：（设 $n = b_1b_2b_3... ...b_{32};$ ）

0 b 2 0 b 4 . . . . . . 0 b 32 ≪ 1 = b 2 0 b 4 0... . . . b 32 0

$0b_20b_4... ... 0b_{32} \ll 1 = b_20b_40... ... b_{32}0$

\cup

$\cup$

b 1 0 b 3 0... . . . b 31 0 ≫ 1 = 0 b 1 0 b 3 . . . . . . 0 b 31

$b_10b_30... ... b_{31}0 \gg 1 = 0b_10b_3... ... 0b_{31}$

=

$=$

b 2 b 1 b 4 b 3 . . . . . . b 32 b 31

$b_2b_1b_4b_3... ...b_{32}b_{31}$

从上式可以看出, 第一行将相邻两位进行了交换.

line 2: n = ((n & 0x33333333) << 2) | ((n & 0xCCCCCCCC) >> 2);

Hex	Bin
0x33333333	0b 0011 0011 0011 0011 0011 0011 0011 0011
0xCCCCCCCC	0b 1100 1100 1100 1100 1100 1100 1100 1100

经line 1处理后, $n = b_2b_1b_4b_3b_6b_5... ...b_{30}b_{29}b_{32}b_{31};$

00 b 4 b 3 00 b 8 b 7 . . . . . . 00 b 32 b 31 ≪ 2 = b 4 b 3 00 b 8 b 7 00 . . . . . . b 32 b 31 00

$00b_4b_300b_8b_7... ... 00b_{32}b_{31} \ll 2 = b_4b_300b_8b_700 ... ... b_{32}b_{31}00$

\cup

$\cup$

b 2 b 1 00 b 6 b 5 00 . . . . . . b 30 b 29 00 ≫ 2 = 00 b 2 b 1 00 b 6 b 5 . . . . . . 00 b 30 b 29

$b_2b_100b_6b_500 ... ... b_{30}b_{29}00 \gg 2 = 00b_2b_100b_6b_5 ... ... 00b_{30}b_{29}$

=

$=$

b 4 b 3 b 2 b 1 b 8 b 7 b 6 b 5 . . . . . . b 32 b 31 b 30 b 29

$b_4b_3b_2b_1b_8b_7b_6b_5 ... ... b_{32}b_{31}b_{30}b_{29}$

从上可也看出, 经line 2处理后, 每个字节中前四位和后四位完成了交换位置.原本第一个字节应该是 $b_1b_2b_3b_4b_5b_6b_7b_8$ , 现在变成了 $b_4b_3b_2b_1b_8b_7b_6b_5$ .

line3: n = ((n & 0x0F0F0F0F) << 4) | ((n & 0xF0F0F0F0) >> 4);

Hex	Bin
0x0F0F0F0F	0b 0000 1111 0000 1111 0000 1111 0000 1111
0xF0F0F0F0	0b 1111 0000 1111 0000 1111 0000 1111 0000

经line 2处理后, $n = b_4b_3b_2b_1b_8b_7b_6b_5 ... ... b_{32}b_{31}b_{30}b_{29};$

0000 b 8 b 7 b 6 b 5 . . . . . . 0000 b 32 b 31 b 30 b 29 ≪ 4

$0000b_8b_7b_6b_5 ... ... 0000b_{32}b_{31}b_{30}b_{29} \ll 4$

= b 8 b 7 b 6 b 5 0000 . . . . . . b 32 b 31 b 30 b 29 0000

$= b_8b_7b_6b_50000 ... ... b_{32}b_{31}b_{30}b_{29}0000$

\cup

$\cup$

b 4 b 3 b 2 b 1 0000 . . . . . . b 28 b 27 b 26 b 25 0000 ≫ 4

$b_4b_3b_2b_10000 ... ... b_{28}b_{27}b_{26}b_{25}0000 \gg 4$

= 0000 b 4 b 3 b 2 b 1 . . . . . . 0000 b 28 b 27 b 26 b 25

$= 0000b_4b_3b_2b_1 ... ... 0000b_{28}b_{27}b_{26}b_{25}$

=

$=$

b 8 b 7 b 6 b 5 b 4 b 3 b 2 b 1 . . . . . . b 32 b 31 b 30 b 29 b 28 b 27 b 26 b 25

$b_8b_7b_6b_5b_4b_3b_2b_1 ... ... b_{32}b_{31}b_{30}b_{29}b_{28}b_{27}b_{26}b_{25}$

由上分析可知, 经line 3处理后, 每个字节完全完成了翻转.由原本的 $b_1b_2b_3b_4b_5b_6b_7b_8$ 翻转成了 $b_8b_7b_6b_5b_4b_3b_2b_1$ .

line 4: n = ((n & 0x00FF00FF) << 8) | ((n & 0xFF00FF00) >> 8);

Hex	Bin
0x00FF00FF	0b 0000 0000 1111 1111 0000 0000 1111 1111
0xFF00FF00	0b 1111 1111 0000 0000 1111 1111 0000 0000

经 line 3后, $n = b_8b_7b_6b_5b_4b_3b_2b_1 ... ... b_{32}b_{31}b_{30}b_{29}b_{28}b_{27}b_{26}b_{25}$

从上表可以看出, 类似于line 1~3, line 4将会完成第一字节和第二字节的交换, 第三字节和第四字节的交换.

即, 经line 4处理后, $n = b_{16}b_{15}b_{14}b_{13}b_{12}b_{11}b_{10}b_9b_8b_7b_6b_5b_4b_3b_2b_1$
$b_{32}b_{31}b_{30}b_{29}b_{28}b_{27}b_{26}b_{25}b_{24}b_{23}b_{22}b_{21}b_{20}b_{19}b_{18}b_{17}$

line 5: n = ((n & 0x0000FFFF) << 16) | ((n & 0xFFFF0000) >> 16);

Hex	Bin
0x0000FFFF	0b 0000 0000 0000 0000 1111 1111 1111 1111
0xFFFF0000	0b 1111 1111 1111 1111 0000 0000 0000 0000

从上可以看出, line 4将会完成第一字节和第二字节的交换, 第三字节和第四字节的交换.

类似于line 1 ~ 4, 本次执行后, $n = b_{32}b_{31}b_{30}b_{29}b_{28}b_{27}b_{26}b_{25}b_{24}b_{23}b_{22}b_{21}b_{20}b_{19}b_{18}b_{17}$
$b_{16}b_{15}b_{14}b_{13}b_{12}b_{11}b_{10}b_9b_8b_7b_6b_5b_4b_3b_2b_1$

3.5 Single Number

Given an array of integers, every element appears twice except for one. Find that single one.

Note:
Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?

原题链接: https://leetcode.com/problems/single-number/

题目大意: 在给定的整数数组中, 除了一个元素, 其余元素都出现两次, 找出这个元素.注意, 算法应该是限行时间复杂度, 并空间复杂度是 $O(1)$ .

代码如下:

int singleNumber(int* nums, int numsSize) {
    if ((NULL == nums) || (0 == numsSize)) {
        return NULL;
    }

    int single = *nums;
    for (int i = 1; i < numsSize; ++i) {
        single ^= nums[i];
    }

    return single;
}

思路很简单, 就是前面提到的异或(相同则为0, 不同则为1)操作.

假设, $Array = \lbrace a_0, a_1, ... ..., a_n \rbrace$ ,则将所有元素做异或操作 $num = a_0 \oplus a_1 ... ... \oplus a_{n-1} \oplus a_n$ .

由于异或具有交换性,则各个元素的位置其实无关紧要,我们可以假设, $\lbrace a_0, a_1\rbrace; \lbrace a_2, a_3\rbrace;... ...;\lbrace a_{n-2}, a_{n-1}\rbrace;$ 是相同的元素.最后一个元素 $a_n$ 是待找到的元素.

则

a 0 \oplus a 1 = 0; a 1 \oplus a 2 = 0; . . . . . .; a n - 2 \oplus a n - 1 = 0

$a_0 \oplus a_1 = 0; a_1 \oplus a_2 = 0; ... ...; a_{n-2}\oplus a_{n-1}=0$

则

n u m = 0 \oplus 0 . . . . . . \oplus 0 \oplus a n = 0 \oplus a n = a n

$num = 0 \oplus 0 ... ... \oplus 0 \oplus a_n=0 \oplus a_n = a_n$

原文链接：https://blog.csdn.net/sunbibei/article/details/50124191

一、位运算

1、 基本操作

2、 组合操作

三、 简单运用

1、基本操作

2、组合操作

三、简单运用