典型相关分析由Hotelling提出,其基本思想和主成分分析非常相似。
首先在每组变量中找出变量的线性组合,使得两组的线性组合之间具有最大的相关系数;
然后选取和最初挑选的这对线性组合不相关的线性组合,使其配对,并选取相关系数最大的一对;
如此继续下去,直到两组变量之间的相关性被提取完毕为止。
被选出的线性组合配对称为典型变量,它们的相关系数称为典型相关系数。典型相关系数度量了这两组变量之间联系的强度。

典型相关步骤: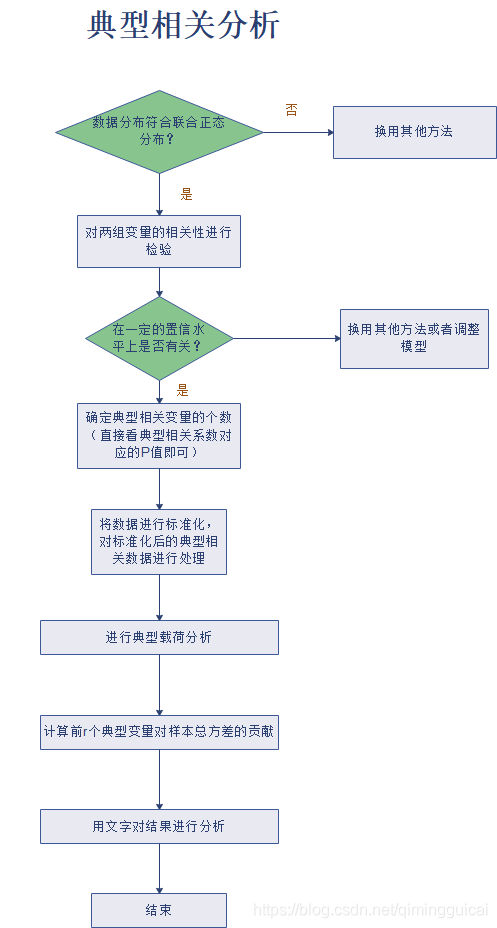
(可以假设符合正态分布)
SPSS操作:
1. 导入数据并确定数据类型为标度
2. 分析-相关-典型相关性
3. 将数据移动到对应的集合(注意运行需要python)
4. 导出结果并进行分析
图标分析指标(AB重要):
A. 标题典型相关性改为典型相关系数
第一列表示相关系数,最后一列表示p值
p值与置信水平挂钩(可以看5-1的相关系数)
B. 两个集合的标题改为“(非)标准化典型相关变量对应的线性组合系数”, 对应订正
看显著的典型相关变量就行 不显著的不用看
非标准化的系数会受到量纲影响,看标准化的会更好
最后要能知道y跟哪些x是相关的
C. (更深层次)载荷分析:
解释典型载荷(最后一个矩阵只有第一行显著,二三不用看;123列对应的就是体重腰围和脉搏)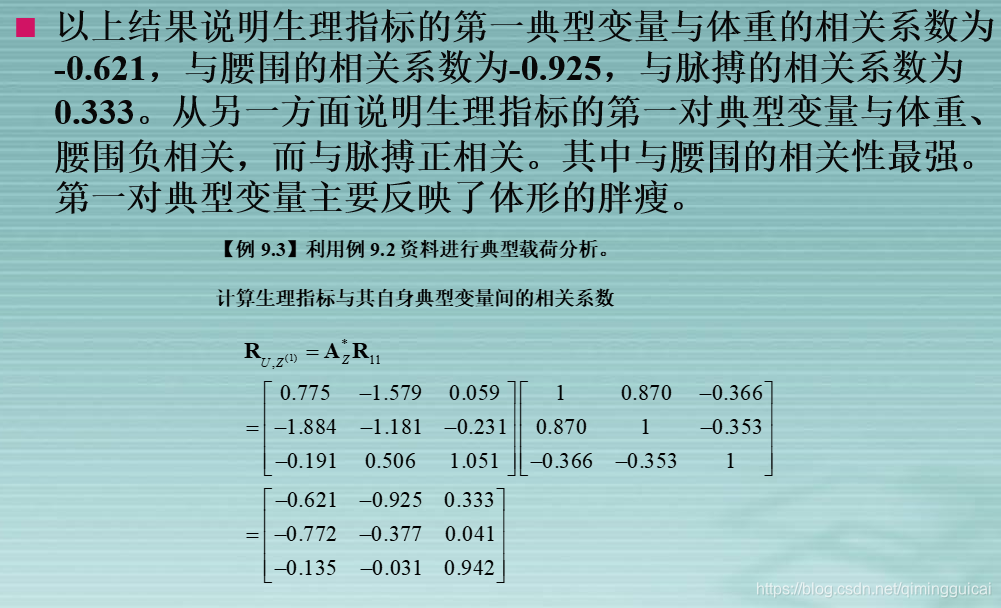
D. 典型冗余分析
关注自身的即可(看一三列
典型冗余分析表示的是解释程度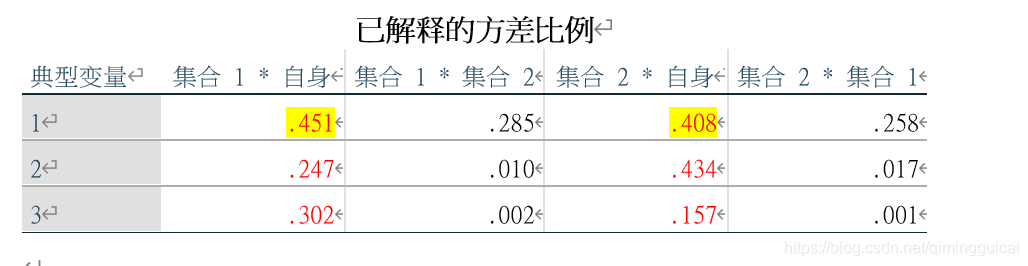
版权声明:本文为qimingguicai原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。