对于一个连续的周期信号,可以将其分解为一组频率不同的三角函数信号的线性组合,这就是傅里叶级数的本质,将信号从时域投影到频域中的不同频段上来完成分解。
当这个周期信号的周期趋近于无穷大时,傅里叶级数就变成了傅里叶变换。此时的信号本质上是一个连续非周期信号,傅里叶变换的意义就在于对其进行分解,同样也是以一组三角函数作为正交基,并通过这组三角函数基的线性组合来表示原信号。数学表达为:
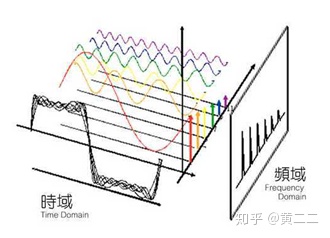
由于三角函数是一个无限长的信号,在时域上不具有局部性,因此以其作为正交基对信号进行拟合时,具有以下两个不足:第一,对于突变信号,如阶跃信号或尖峰信号,其需要大量的三角函数基进行组合才能完成较好的信号拟合;第二,由于三角函数不具备在时域上的局部性,因此在对信号进行傅里叶变换时,仅仅只能获取到信号在频域上的分布信息,并不能获取到这些不同频率的信号分量在时域上出现的位置。因此傅里叶变换对于非平稳信号的分解会遗失其在时域上的变化信息。
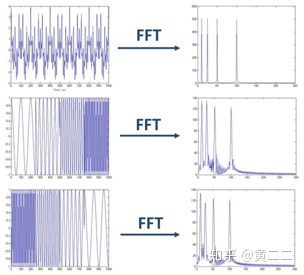
小波变换就是为了解决对非平稳信号的分解问题而产生的数学方法。相比于傅里叶变换使用一组无限长的三角函数基进行信号拟合,小波变换使用的是一组正交的、迅速衰减的小波函数基进行信号拟合。这种小波函数基可通过其尺度变量和平移变量,获得不同的频率和时间位置。因此在利用这种小波函数基对信号进行分解时,可以用较少的小波函数基就拟合出突变信号(稀疏编码特性),同时也能获得不同频率的信号分量在时域上的出现位置。
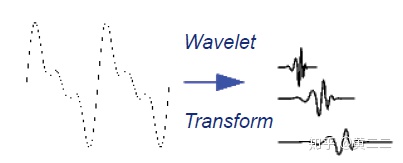
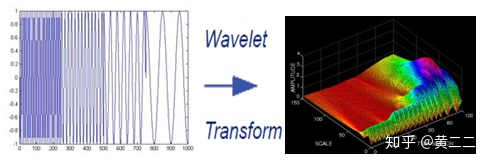
用于生成一组不同频率和时移的小波函数的小波函数
可进行小波变换的对象是平方可积的信号,也即是位于希尔伯特空间中的一个函数。希尔伯特空间保证了在空间中的每一个函数,都可由该空间中的其他函数线性组合得到。
小波变换值,也即是用于拟合原始信号的小波函数基的系数,可通过计算原始信号与各小波函数基的内积得到。其意义为原始信号在各个小波函数基上的投影值,投影值越大,说明对应的小波信号所携带的原始信号的特征信息的比例越大。数学表达如下:
其中,
在实际应用中,由于计算机的处理对象为离散数据,因此在使用小波变换时,一般指的都是离散小波变换。因此对于上式,可写成离散形式:
其中,
从数学的角度理解,在小波变换中,一个位于希尔伯特空间中的函数,可以分解成一个尺度函数和一个小波函数,其中尺度函数对应原始函数中的低频部分,小波函数对应原始函数中的高频部分。通过尺度函数可以构建对原始信号的低通滤波器,通过小波函数可以构建对原始信号的高通滤波器。
从信号处理的角度理解,在小波变换中,信号可通过信号滤波器分解为高频分量(高频子带(subband))和低频分量(低频子带(subband)),高频子带又称为细节(detailed)子带,低频子带又称为近似(approximate)子带。细节子带是由输入信号通过高通滤波器后再进行下采样得到的,近似子带是由输入信号通过低通滤波器后再进行下采样得到的。
小波变换是这样一个过程:首先将原始信号作为输入信号,通过一组正交的小波基分解成高频部分和低频部分,然后将得到的低频部分作为输入信号,又进行小波分解,得到下一级的高频部分和低频部分,以此类推。随着小波分解的级数增加,其在频域上的分辨率就越高。这就是多分辨率分析(MRA,MultiResolution Analysis)。
离散小波变换在逐级分解时,由尺度函数所张成的空间为:
其中
离散小波变换在逐级分解时,由小波函数所张成的空间为:
其中
由上式可知,分解级数越高,信号在时域和频域的分辨率就越高,包含的信息也就越多。
又根据上式,对于
其中
在小波变换中,若令尺度参数为
在二进小波变换中,各级小波分解时,相邻级数的尺度函数之间满足关系:
即是:
相邻级数的小波函数和尺度函数之间满足关系:
即是:
其中,
在小波变换中,紧支撑小波基是性质较好的一类小波基,紧支撑(Compact Support)函数是指这样的一类函数:其自变量仅在0附近的取值范围内能得到非零函数值,而在其他区间取值,则得到的函数值全为零。能得到非零函数值的自变量取值区间被称为该函数的支撑区间。一个函数的支撑区间长度主要由其尺度参数决定。支撑区间越大,计算复杂度越高,边界拖尾效应越明显。不仅如此,支撑区间越大,会产生更多的高幅值小波系数,关于这个结论的解释,可参考傅里叶变换使用无限长(支撑区间大)的三角函数基进行信号拟合的情况,相比于使用信号迅速衰减(支撑区间小)的小波基,三角函数基拟合信号时需要更多的数量。因此在选择小波基时,以支撑长度较短的小波基为宜。此外,小波基的正交性也是一类重要的性质,它确保了信号的分解没有冗余(最优分解)。
在小波变换中,另一个重要的概念是消失矩。小波函数的消失矩定义如下:
若:
则称该小波函数具有N阶消失矩。其中,
然而小波变换仍存在着不足之处,由于小波变换在每级信号分解时仅仅对低频子带进行分解,因此无法对高频子带的信息进行同样高分辨率的提取。
小波包分解(Wavelet Packet Decomposition),又称为最优子带树结构(Optimal Subband Tree Structuring)正是对小波变换的进一步优化。其主要的算法思想是:在小波变换的基础上,在每一级信号分解时,除了对低频子带进行进一步分解,也对高频子带进行进一步分解。最后通过最小化一个代价函数,计算出最优的信号分解路径,并以此分解路径对原始信号进行分解。
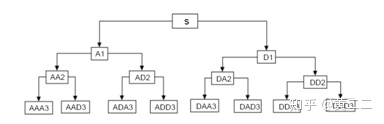
同样地,在二进小波包变换中,各级小波包分解时,相邻级数的尺度函数和小波函数之间也具有递推关系。
记小波包变换中的父小波
于是上述的递推关系可以表述如下:
即是:
其中
在小波包变换中,常用的代价函数为信息熵函数。最小化代价函数,也即是最大化逐级信号分解的信息熵。
无论是小波变换还是小波包变化,一个重要的环节是选择合适的小波函数基进行信号分解。常用的几类小波函数基包括:
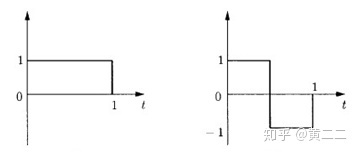
Haar小波:Haar函数是最简单的一个小波函数,其具有紧支撑性和正交性,函数图像为在支撑区间[0,1)上的单个矩形波。Haar小波在时域上不连续,作为基本小波时性能不是很好。
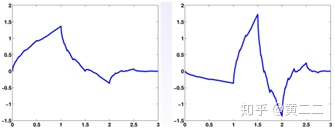
Daubechies小波:通常简称为
Biorthogonal小波:双正交小波,使用对偶的两个小波分别用于信号的分解和重构。双正交小波与正交小波的区别在于,在正交小波中,由基本小波的伸缩和平移所产生的一族小波基函数之间完全正交。而在双正交小波中,由基本小波的伸缩所产生的一族小波基函数完全正交,由基本小波的平移所产生的一族小波基函数则不正交。双正交小波借由牺牲一部分的正交性,来减少基本小波平移产生小波基时需满足的约束(扩大函数空间),从而使小波可以通过平移来获取线性相位(在函数空间中可取到具有线性相位的函数),以得到精确重构信号所需的对称性。双正交小波的作用过程可以描述为:首先对输入信号使用一个双正交小波进行正交分解,然后在该双正交小波的对偶空间中寻找一个具有线性相位的对偶小波进行对输入信号的非正交重构。双正交小波具备正则性和紧支撑性,其重构支撑区间长度为
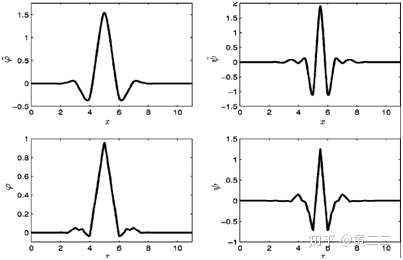
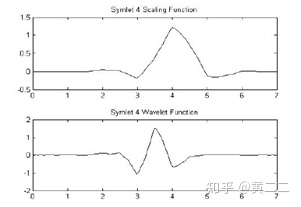
Symlets小波:通常简称为
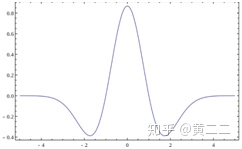
Mexican Hat小波:Mexican函数为Gaussian函数的二阶导数,形似墨西哥帽的截面,它在时域和频域上都具有很好的局部性,但不存在尺度函数,因此该小波函数不具备正交性。
在选择合适的小波函数基时,需要考虑的因素除了小波的支撑区间大小、小波的消失矩之外,还需考虑其对称性、正则性和相似性。小波的对称性主要体现在保证信号重构时不会产生相位畸变,即是不会产生重构信号的相位失真。小波的正则性保证了信号的光滑和可微性,对于大部分小波而言(非全部),其与消失矩存在关系:小波的消失矩越大,正则性也就越大。最后,选择与输入信号的波形相似性高的小波,意义在于使数据压缩和降噪变得更容易(信号的拟合和分解都更容易)。
关于小波分解的应用:
由于小波分解的稀疏编码特性,其可用于数据压缩,主要做法为:将信号进行小波分解,并将较小的小波系数置零。相当于将不重要(特征不明显)的信息分量去除,达到数据精简的效果。
小波分解也可用于信号滤波,主要做法为:将信号进行小波分解,并将特定级数以上的小波系数置零。相当于将高分辨率的信息分量去除,达到数据平滑的效果。
小波分解还可用于信号降噪,主要做法为:将信号进行小波分解,并通过设置一个阈值,将其中低于阈值的小波系数置零。相当于将信号中占成分比例较低的噪声部分去除。
小波包分解的应用与小波分解同理。