目录
1.栈在括号匹配中的应用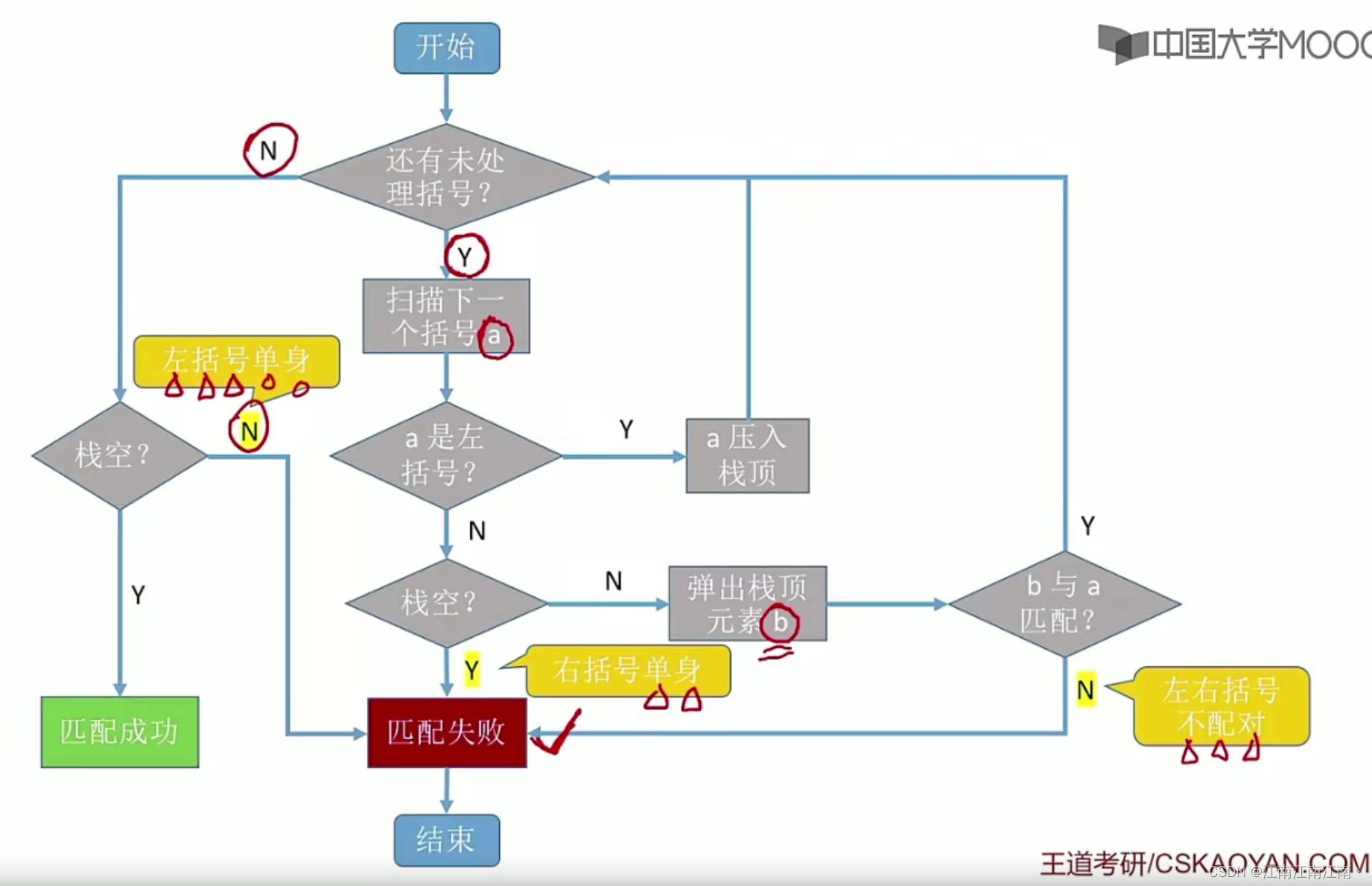
#include<iostream>
#include<string>
#define maxSize 10
using namespace std;
//定义顺序栈,采用静态数组
typedef struct sqStack {
string data;
int top;
}sqStack;
//初始化栈
bool initStack(sqStack& S) {
S.top = -1;
return true;
}
//进栈
bool push(sqStack& S, char e) {
if (S.top == maxSize - 1) return false;
S.data[++S.top] = e;
return true;
}
//出栈
bool pop(sqStack& S, char& e) {
if (S.top == -1) return false;
e = S.data[S.top--];
return true;
}
//判断栈空
bool emptyStack(sqStack S) {
if (S.top == -1) return false;
else return true;
}
//括号匹配
bool bracket(string str) {
sqStack S;
initStack(S);
//获得字符串长度
int length = str.length();
//保存栈顶的元素
char topElem;
//遍历字符串
for (int i = 0; i < length; i++) {
//当前是'{'进栈
if (str[i] == '{') push(S, str[i]);
//当前是'}'出栈,进行匹配
else if (str[i] == '}') {
pop (S, topElem);
if (topElem != '{') return false;
}
//当前是'['进栈
else if (str[i] == '[') push(S, str[i]);
//当前是']'出栈,进行匹配
else if (str[i] == ']') {
pop (S, topElem);
if (topElem != '[') return false;
}
//当前是'('进栈
else if (str[i] == '(') push(S, str[i]);
//当前是')'出栈,进行匹配
else if (str[i] == ')') {
pop (S, topElem);
if (topElem != '(') return false;
}
}
//循环结束后,栈空则匹配成功
if (emptyStack) return true;
else return false;
}2.栈在表达式求值中的运用
前缀表达式:运算符在两个操作数前面
+a b //操作数1
* c d //操作数2
- + a b * c d 中缀表达式:运算符在两个操作数中间
a + b - c * d
后缀表达式:运算符在两个操作数后面
a b + //操作数1
c d * //操作数2
a b + c d * -2.1.中缀表达式转换后缀表达式
- 确定中缀表达式的各个运算符的运算顺序
- 选择下一个运算符,按照【左操作数 右操作数 运算符】的方式组成一个新的操作数(整体)
- 如果还有运算符,则重复2
- "左优先"原则:只要左边的运算符能先计算,则优先计算左边(转换后的后缀表达式不唯一,采用左优先原则可以保证后缀唯一)
中缀表达式:((15 / (7 - (1 + 1))) * 3) - (2 + (1 + 1))
后缀表达式:
(1)1 1 +
(2)7 1 1 + -
(3)15 7 1 1 + - /
(4)3 15 7 1 1 + - / * //左操作数
(5)1 1 +
(6)2 1 1 + +
(7)3 15 7 1 1 + - / * 2 1 1 + + -2.2.后缀表达式的计算方法
从左往右扫描,每遇到一个运算符,就让运算符前面最近的两个操作数执行对应运算,合并为一个操作数
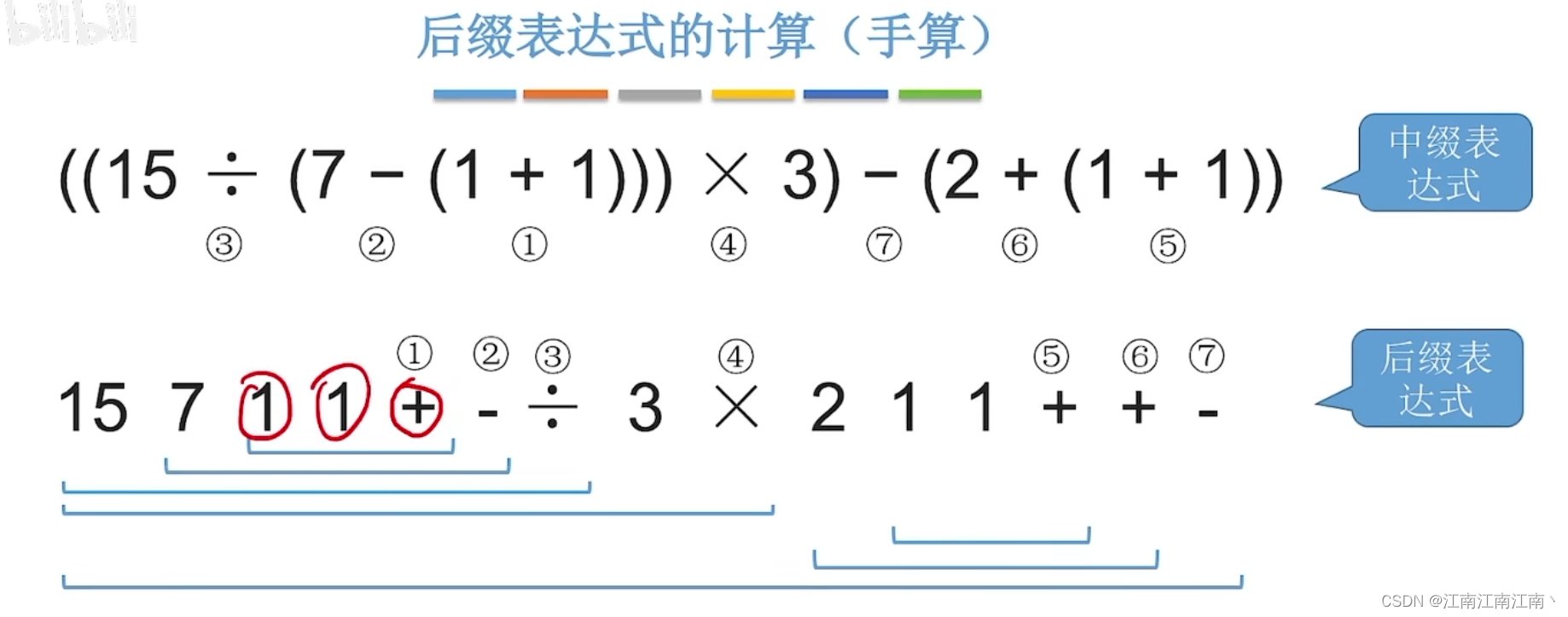
//括号表示括号内为一个整体操作数
//3 15 7 1 1 + - / * 2 1 1 + + -
(1)1 1 +
(2)7 (1 1 +) -
(3)15 (7 (1 1 +) -) /
(4)3 (15 (7 (1 1 +) -) /) *
(5)1 1 +
(6)2 (1 1 +)
(7)(3 (15 (7 (1 1 +) -) /) *) (2 (1 1 +)) - 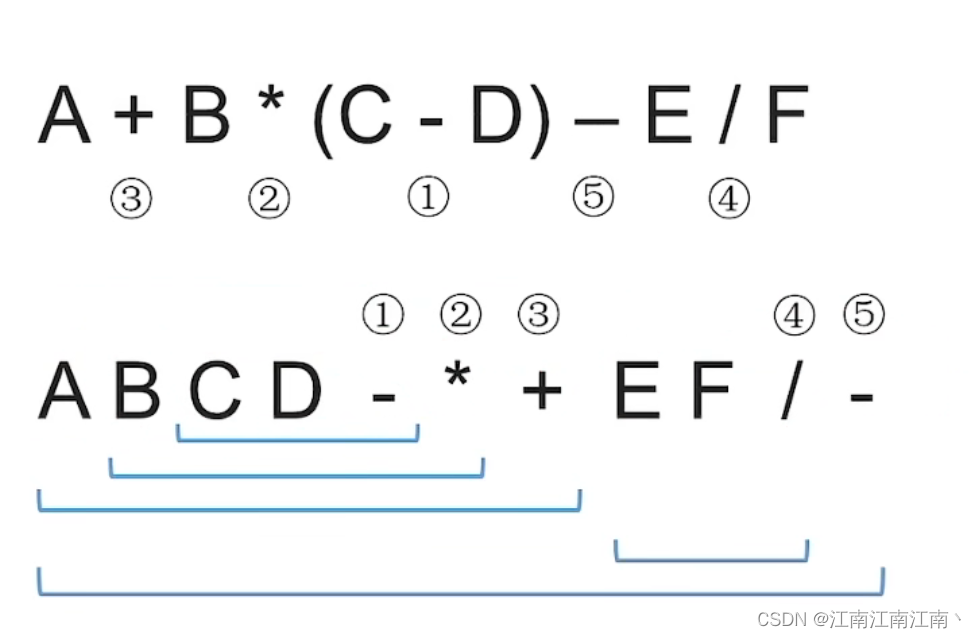
//括号表示括号内为一个整体操作数
//A B C D - * + E F / -
(1)C D -
(2)B (C D -) *
(3)A B (C D -) * +
(4)E F /
(5)(A B (C D -) * +) (E F /) -2.3.中缀表达式转换前缀表达式
- 确定中缀表达式的各个运算符的运算顺序
- 选择下一个运算符,按照【 运算符 左操作数 右操作数】的方式组成一个新的操作数(整体)
- 如果还有运算符,则重复2
- "右优先"原则:只要右边的运算符能先计算,则优先计算右边(转换后的后缀表达式不唯一,采用右优先原则可以保证后缀唯一)
中缀表达式:A + B * (C - D) - E / F
前缀表达式:
(1)/ E F
(2)- C D
(3)* B - C D
(4)+ A * B - C D
(5)- + A * B - C D / E F2.4. 中缀表达式转后缀表达式(机算——栈)
- 初始化一个栈,用于保存暂时还不能确定运算顺序的运算符
- 从左到右依次处理各个元素。有三种情况
- 遇到操作数。直接加入到后缀表达式
- 遇到界限符。遇到"("直接入栈;遇到")"依次弹出站内运算符并且假如后缀表达式,直到弹出"("为止。注意:"("不加入后缀表达式
- 遇到运算符。依次弹出栈中优先级高于或等于当前运算符的所有运算符,并加入后缀表达式。若碰到"("或栈空则停止。之后再把当前运算符入栈
- 按照上述方法处理完所有字符后,依次弹出栈中剩余运算符,并假如后缀表达式中
A + B - C * D / E + F
(1)
扫描到'A':'A'是操作数,直接加入后缀表达式
后缀表达式:A
栈:空
(2)
扫描到'+':'+'是运算符,此时栈空,入栈
后缀表达式:A
栈:+
(3)
扫描到'B':'B'是操作数,直接加入后缀表达式
后缀表达式:A B
栈:+
(4)
扫描到'-':'-'是运算符,因为栈顶元素为'+',与'-'同优先级,因此,弹出'+'加入后缀表达式后,将'-'入栈
后缀表达式:A B +
栈:-
(5)
扫描到'C':'C'是操作数,直接加入后缀表达式
后缀表达式:A B + C
栈:-
(6)
扫描到'*':'*'是运算符,因为栈顶元素为'-',优先级<'*',因此,将'*'入栈
后缀表达式:A B + C
栈:- *
(7)
扫描到'D':'D'是操作数,直接加入后缀表达式
后缀表达式:A B + C D
栈:- *
(8)
扫描到'/':'/'是运算符,因为栈顶元素为'*',与'/'同优先级 && 优先级>'-',因此,弹出'*'加入后缀表达式后,将'/'入栈
后缀表达式:A B + C D *
栈:- /
(9)
扫描到'E':'E'是操作数,直接加入后缀表达式
后缀表达式:A B + C D * E
栈:- /
(10)
扫描到'+':'+'是运算符,因为栈顶元素为'/',优先级<'/' && 优先级 = '-',因此,依次弹出'/''-'加入后缀表达式后,将'+'入栈
后缀表达式:A B + C D * E / -
栈:+
(11)
扫描到'F':'F'是操作数,直接加入后缀表达式
后缀表达式:A B + C D * E / - F
栈:+
(12)
所有符号全部扫描完毕,清空栈中元素,并使其加入后缀表达式中
后缀表达式:A B + C D * E / - F +
栈:空A + B * (C - D) - E / F
(1)
扫描到'A':'A'是操作数,直接加入后缀表达式
后缀表达式:A
栈:空
(2)
扫描到'+':'+'是运算符,此时栈空,入栈
后缀表达式:A
栈:+
(3)
扫描到'B':'B'是操作数,直接加入后缀表达式
后缀表达式:A B
栈:+
(4)
扫描到'*':'*'是运算符,栈中元素'+' < '*','*'入栈
后缀表达式:A B
栈:+ *
(5)
扫描到'(':'('是界限符,入栈
后缀表达式:A B
栈:+ * (
(6)
扫描到'C':'C'是操作数,直接加入后缀表达式
后缀表达式:A B C
栈:+ * (
(7)
扫描到'-':'-'是运算符,此时栈顶元素为'(',入栈
后缀表达式:A B C
栈:+ * ( -
(8)
扫描到'D':'D'是操作数,直接加入后缀表达式
后缀表达式:A B C D
栈:+ * ( -
(9)
扫描到')':')'是界限符,出栈直到出栈元素为'(',加入出栈元素中的运算符
后缀表达式:A B C D -
栈:+ *
(10)
扫描到'-':'-'是运算符,优先级<'*' && 优先级 = '+',依次出栈,并将'-'入栈
后缀表达式:A B C D - * +
栈:-
(11)
扫描到'E':'E'是操作数,直接加入后缀表达式
后缀表达式:A B C D - * + E
栈:-
(12)
扫描到'/':'/'是运算符,优先级>'-',入栈
后缀表达式:A B C D - * + E
栈:- /
(13)
扫描到'F':'F'是操作数,直接加入后缀表达式
后缀表达式:A B C D - * + E F
栈:- /
(14)
扫描完所有字符,依次弹出栈中元素,并将其加入后缀表达式中
后缀表达式:A B C D - * + E F / -
栈:空
2.5.中缀表达式的计算(机算)
用栈实现:
- 初始化两个栈,操作数栈和运算符栈
- 若扫描到操作数,压入操作数栈
- 若扫描到运算符或界限符,则按照“中缀转后缀”相同的逻辑压入运算符栈(期间也会弹出运算符,每当弹出一个运算符时,就需要再弹出两个操作数栈的栈顶元素并执行相应运算,运算结果再压回操作数栈)
A + B - C * D / E + F
(1)
扫描到'A':进操作数栈
操作数栈:A
运算符栈:空
(2)
扫描到'+':运算符栈空,因此,进入运算符栈
操作数栈:A
运算符栈:+
(3)
扫描到'B':进入操作数栈
操作数栈:A B
运算符栈:+
(4)
扫描到'-':运算符栈顶元素为'+',优先级相等,因此,弹出'+'和操作数栈的两个元素计算,计算结果压回操作数栈,后'-'进运算符栈
操作数栈:(A B +)
运算符栈:-
(5)
扫描到'C':进入操作数栈
操作数栈:(A B +) C
运算符栈:-
(6)
扫描到'*':运算符栈顶元素为'-',优先级<'*',因此,'*'进栈
操作数栈:(A B +) C
运算符栈:- *
(7)
扫描到'D':进入操作数栈
操作数栈:(A B +) C D
运算符栈:- *
(8)
扫描到'/':运算符栈顶元素为'*',优先级相等,因此,弹出'*'和操作数栈的两个元素计算,计算结果压回操作数栈,后'/'进运算符栈
操作数栈:(A B +) (C D *)
运算符栈:- /
(9)
扫描到'E':进入操作数栈
操作数栈:(A B +) (C D *) E
运算符栈:- /
(10)
扫描到'+':运算符栈中优先级都>='+',因此依次弹出,并将计算结果压入操作数栈中,后将'+'入运算符栈
操作数栈:(A B + C D * E / -)
运算符栈:+
(11)
扫描到'F':进入操作数栈
操作数栈:(A B + C D * E / -) F
运算符栈:+
(12)
扫描完全部字符,弹出运算符栈中所有元素,并计算
A B + C D * E / - F +3.栈在递归中的应用
函数调用的特点:最后被调用的函数最先执行结束
函数调用时,需要用一个栈存储:
- 调用返回地址
- 实参
- 局部变量
4.队列应用
- 树的层次遍历
- 图的广度优先遍历
- 操作系统——FCFS(先来先服务)
5.特殊矩阵的压缩
二维数组拥有随机存储的特性
行优先:

列优先:

注意:矩阵的行号和列号通常从1开始,而数组下标通常由0开始
5.1.对称矩阵的压缩存储
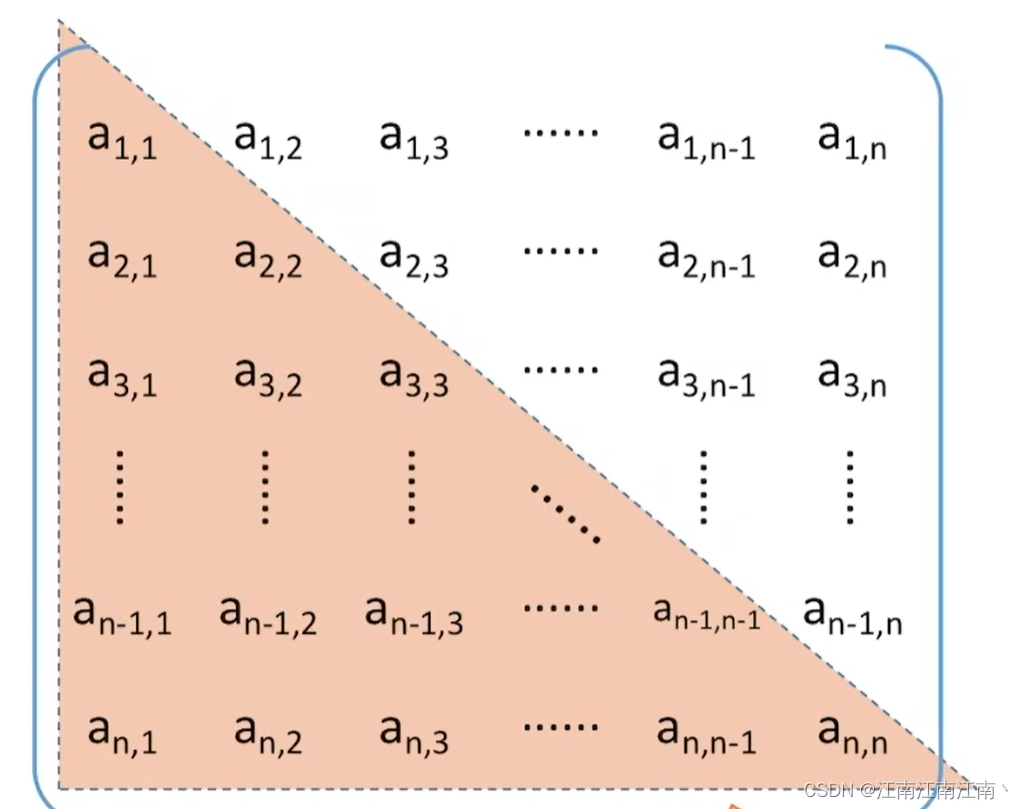
对称矩阵的特点是上三角和下三角的元素一一相等,因此,只要存储对角线元素+上三角元素(或下三角元素)
若存储的是下三角,采用行优先的原则存入数组中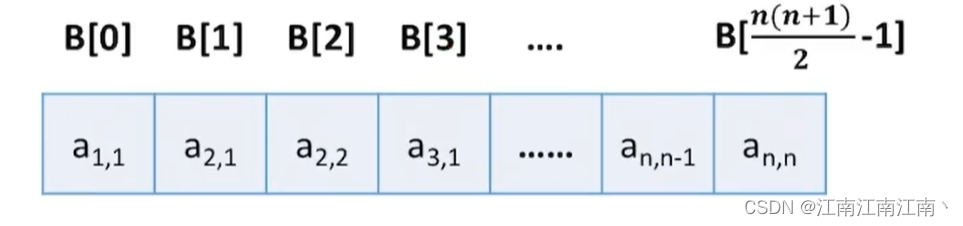
1.数组大小:第一行1个,第二行2个,第三行3个……第n行n个
因此,数组大小为((1 + n) * n ) / 2
2.数组下标和矩阵元素的映射:
矩阵元素:a(i,j)
数组下标B[k]:k = 1 + 2 + …… + (i - 1) + j - 1 (-1是因为数组下标从0开始)
5.2.三角矩阵的压缩存储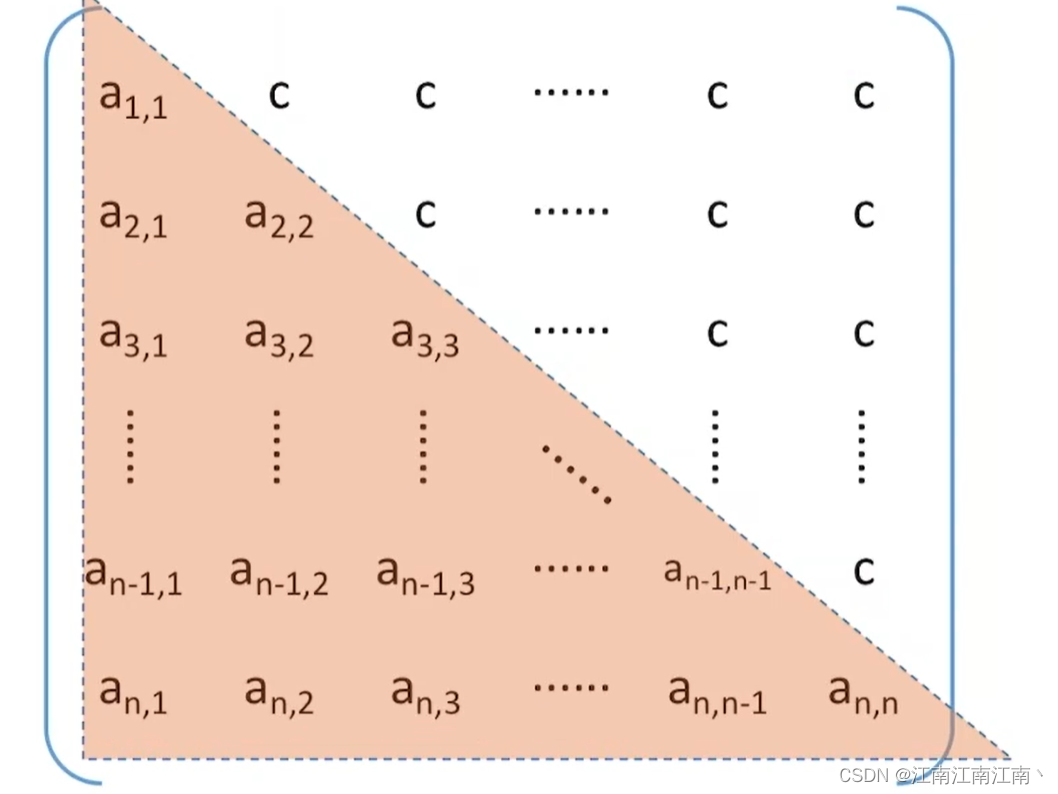
与对称矩阵相同,存储上三角或者下三角,存储完成后,多加一个位置存储C
1.数组大小 ((1 + n) * n ) / 2 + 1
2.数组下标:
访问三角时,与对称矩阵相同;访问c时,访问数组的最后一个元素c
5.3.带状矩阵的压缩存储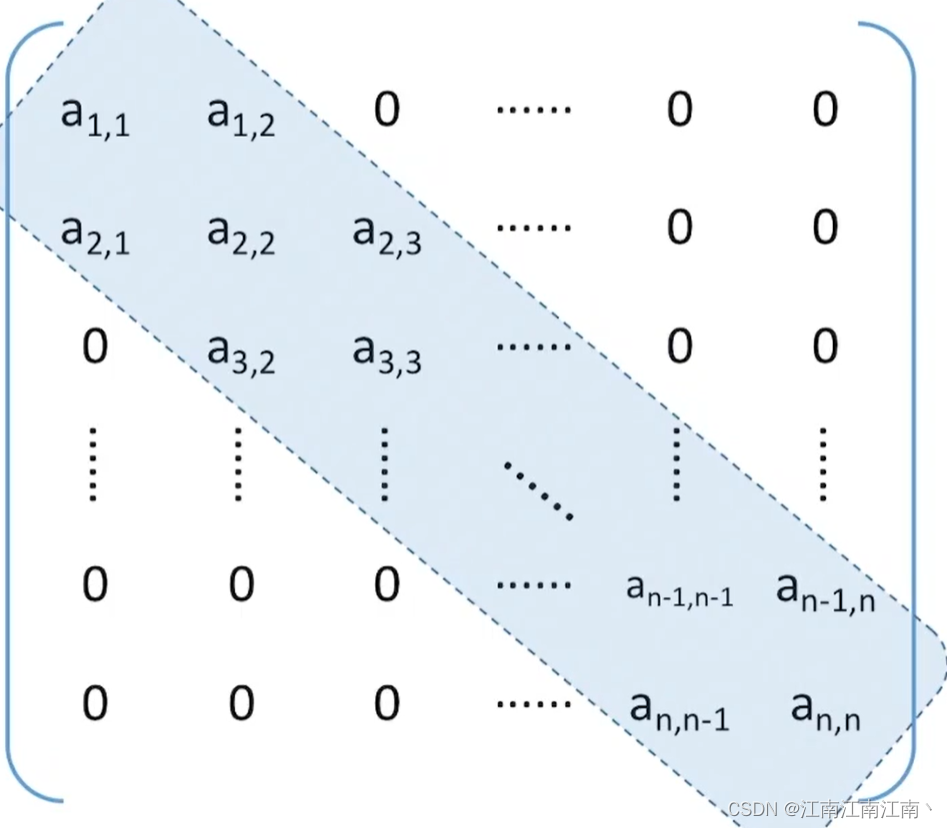
1.存储策略:只存储中间的带状部分
2.特点 :除了第一行和最后一行是两个元素以外,每行是三个元素,因此,共(3n - 2)个元素,数组从0开始,因此,最后一个元素的数组下标为(3n - 3)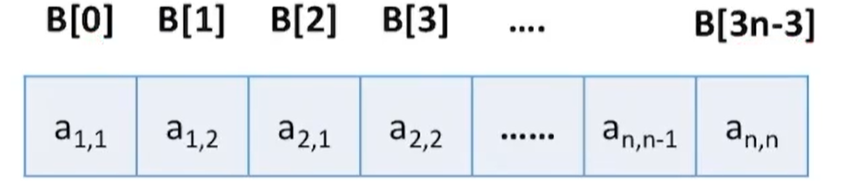
3.元素和数组下标的映射关系:a(i,j)
- 前i - 1行:(i - 1) * 3 - 1
- 第i行:j - i + 2
- a(i,j)是第2i + j - 2个元素
- 数组下标从0开始,因此数组下标为2i + j - 3
4. 已知B[k],如何得到i,j
- 数组下标为k,因此是第k+1个元素
- 前(i - 1)行元素总个数为(i - 1) * 3 - 1
- 前 i 行元素总个数为i * 3 - 1
- (i - 1) * 3 - 1 < k + 1 <= i * 3 - 1
- i = ⌈(k + 2) / 3⌉
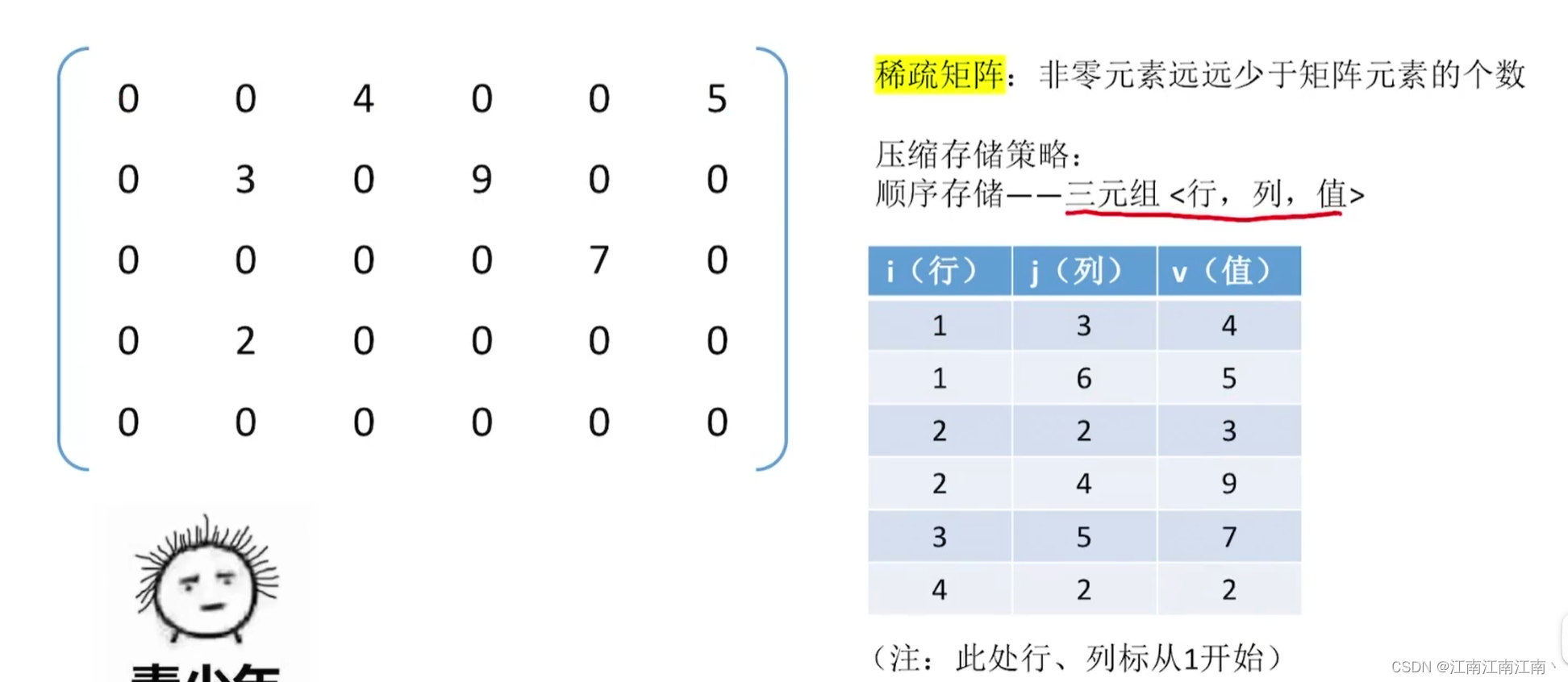
5.4.稀疏矩阵的压缩存储
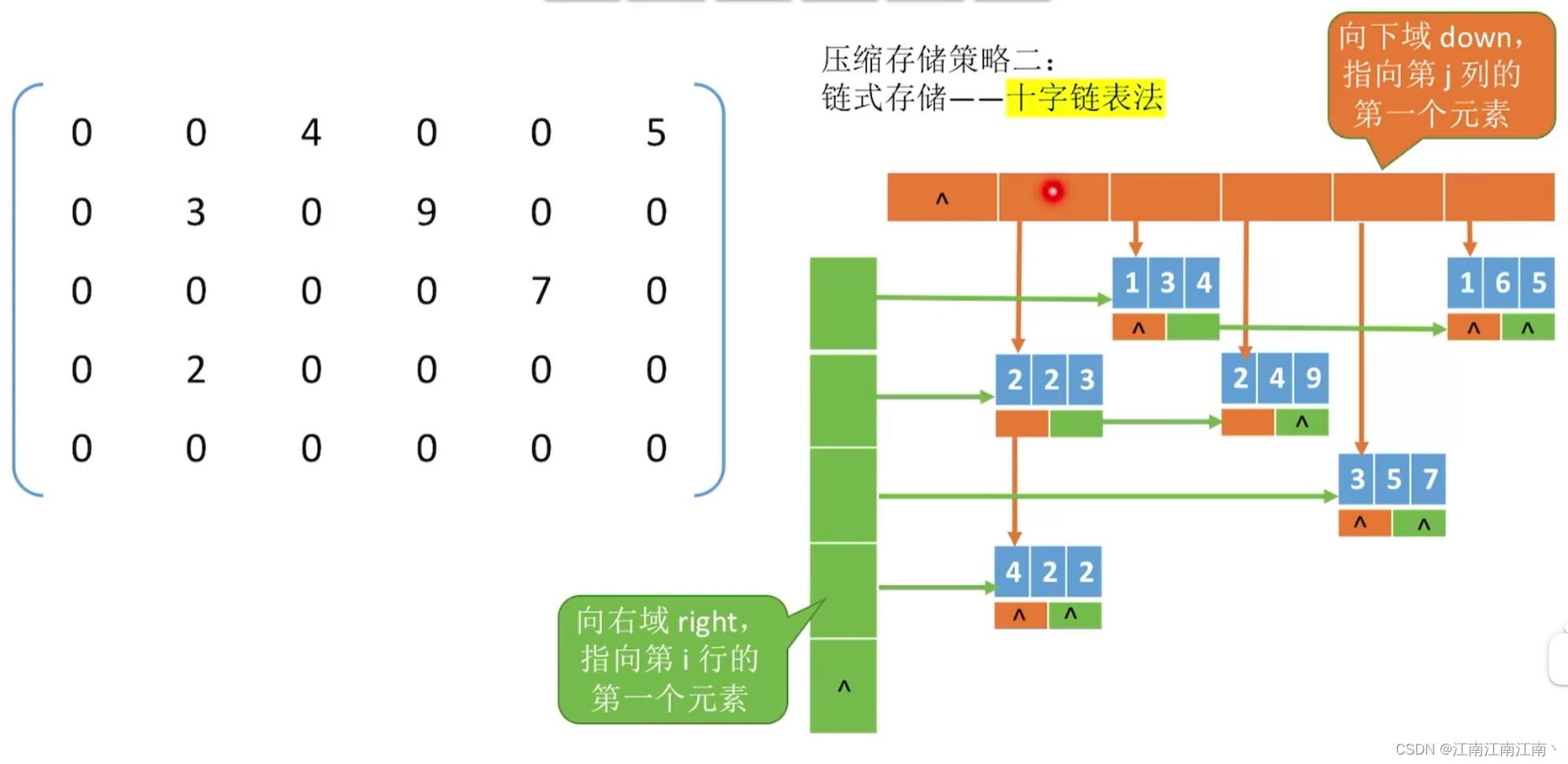
- 顺序存储——三元表
- 链式存储——十字链表
版权声明:本文为JiangNan_1002原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。