动态规划-环形子数组的最大和

Title: 动态规划

Date: 2022-09-04 18:14:31

1、环形子数组的最大和

思路：两种情况：

• case（1）:最大和在中间（这个子数组不是环形，首尾不相连）
• case (2) : 最大和在循环（子数组一部分在首，一部分在尾）

(简而言之：最大子数组不成环 -——也就是maxSum为答案 最大子数组成环 ，那么最小子数组就不会成环 —— (total -minSum) 即为答案

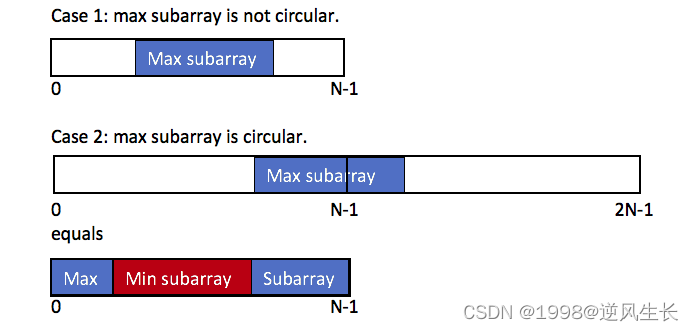
最大的环形子数组和 = max(最大子数组和，数组总和-最小子数组和)

class Solution {
public:
    int maxSubarraySumCircular(vector<int>& nums) {
        int sum=0;
        int s=0;
        int res=INT_MIN;
        for(int i=0;i<nums.size();i++){
            sum+=nums[i];
            s+=nums[i];
            res=max(res,sum);
            if(sum<=0)
                sum=0;
        }//第一种情况下的最大子数组和
        int res1=INT_MAX;
        int sum1=0;
        for(int i=0;i<nums.size();i++){
            sum1+=nums[i];
            res1=min(sum1,res1);//第二种情况下最小子数组和
            if(sum1>=0)
                sum1=0 ;    
        }
        if(s==res1)
            return res;
        else
            return max(s-res1,res);

    }
};

All is Well !!!