最大堆和最小堆

最大堆和最小堆都是由完全二叉树或是近似完全二叉树实现的,每个节点的左 子树和右子树都是一个二叉堆。

最大堆和最小堆的表现形式:可以利用数组的索引来实现。

最大堆:即根节点是此堆中最大的元素

最小堆:即根节点是此堆中最小的元素

最大堆:

初始化最大堆:

首先在构造堆的基本思想就是:利用数组中的索引值来进行数据的存储并设置为二叉树,假设树的节点个数为n，以1为下标开始编号，直到n结束。对于节点i，其父节点为i/2；左孩子节点为i*2，右孩子节点为i*2+1。最后一个节点的下标为n，其父节点的下标为n/2。

即可构建堆。

最大堆插入元素(up):

最大堆的插入节点的思想就是先在堆的最后添加一个节点，然后沿着堆树上升。

在最大堆中插入元素的时候会有比其父节点大,则不满足最大堆的定义,这是就需要调整堆中的位置,因此需要up操作,up操作让插入的子节点跟父节点进行对比,若子节点大于父节点即交换,且索引值k/2,即更新位置,继续重复操作，最后直到维护为最大堆位置。

例如下图，插入节点为60 显然插入的节点后不满足最大堆的性质,则需要维护

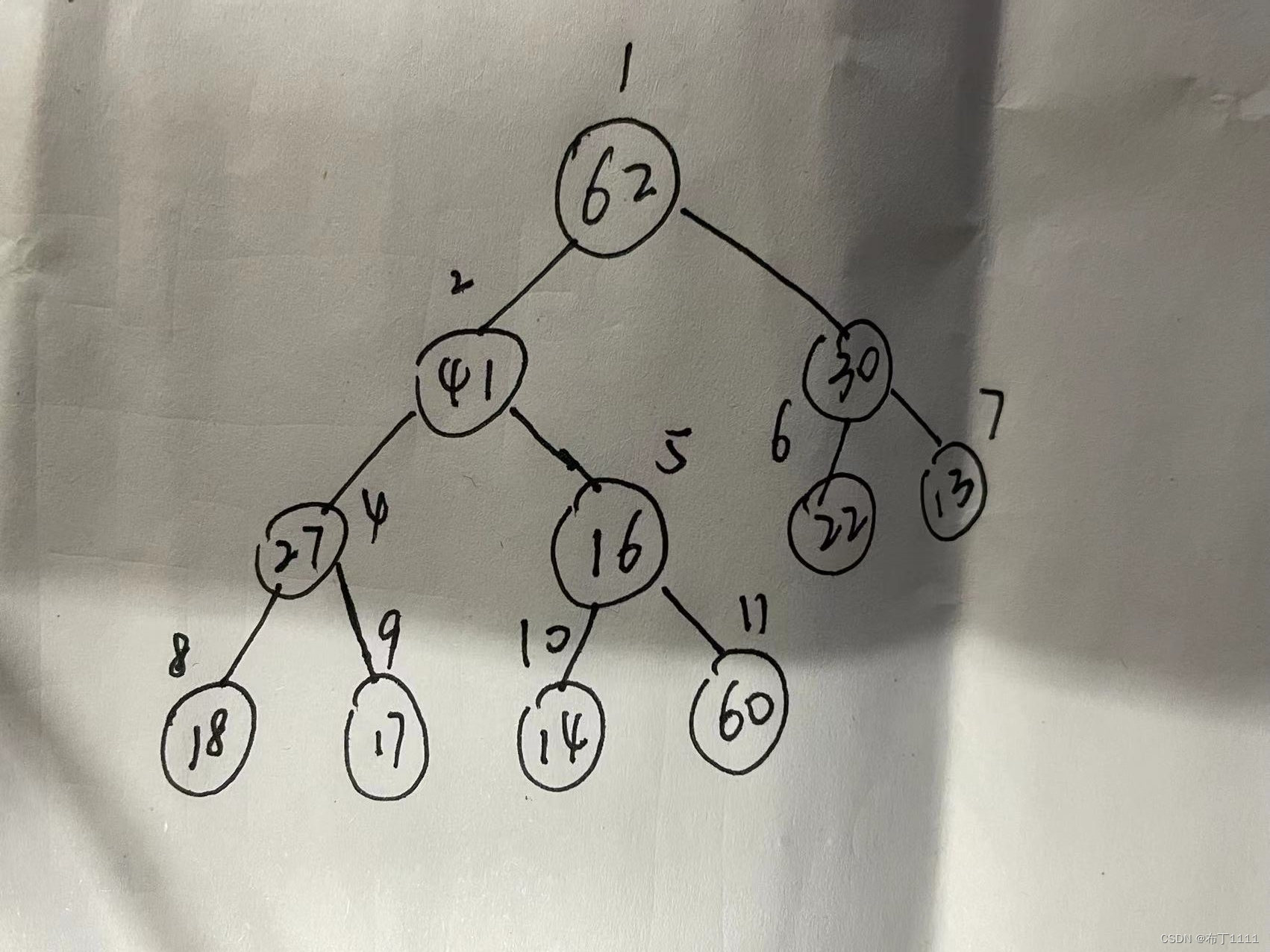
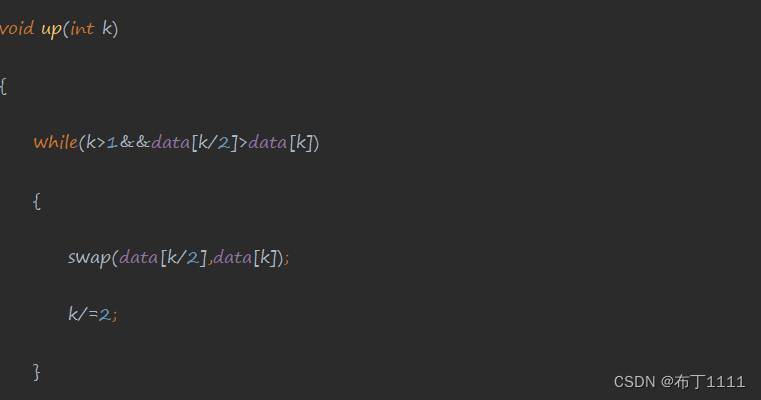
up的代码展示 (需要防止越界则对于k的值一定不能小于1)

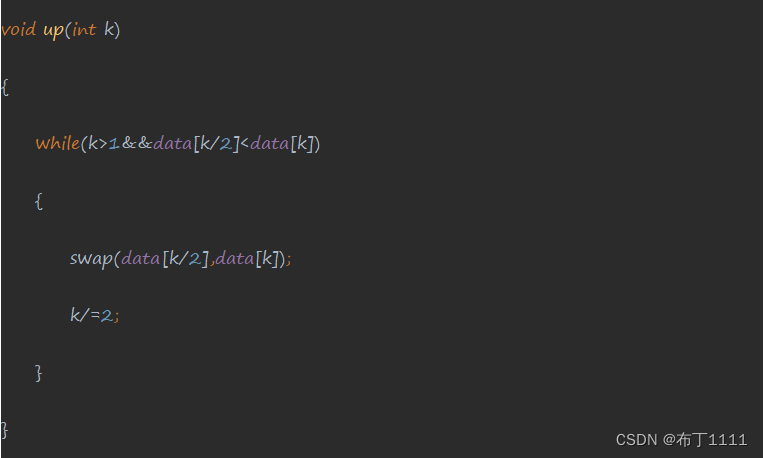
最大堆中删除元素(down)：

最大堆堆顶节点删除思想如下：将堆树的最后的节点提到根结点，然后删除最大值，然后再把新的根节点放到合适的位置。

down的操作代码展示:

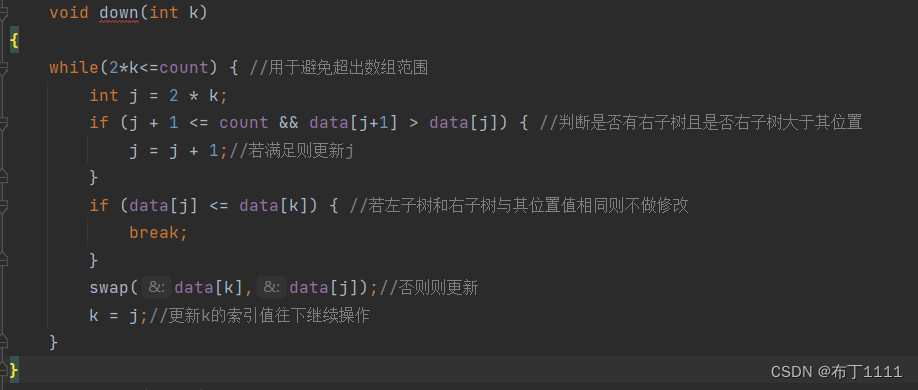
最小堆:

最小堆的构建、插入、删除的过程与最大堆与此类似。

构建方式与最大堆一致

最小堆的插入元素

void insert(int value)//插入元素
    {
        //在尾部插入元素
        data[i] = value;
        count++;
        up(count);
    }

up的函数中只需要修改判断的条件即可

最小堆的删除元素(与最大堆类似)

int pop()//删除元素
    {
        int res = data[1];
        swap(data[1],data[count]);
        count--; //索引值-1
        down(1);
        return res;
    }

利用down来维护最小堆

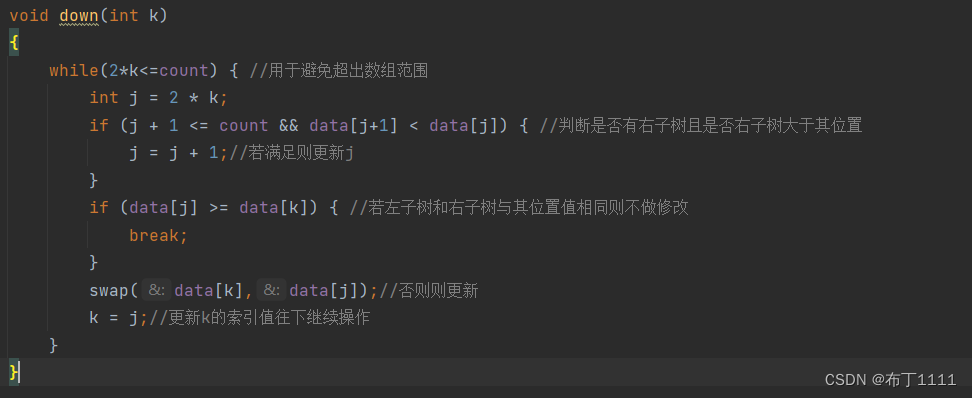
down代码如下:

全部代码:

class myindexheap
{
private:
    int *data;//存放元素
    int count;//存放数组索引
    int capacity;//容量大小
public:
    myindexheap(int capacity)
    {
        data = new int[capacity+1];//初始化数组
        count=0; //初始化索引值
        this->capacity = capacity;//初始化容量
    }
    ~myindexheap()
    {
        delete [] data;
    }
    int size(){
        return count;
    }
    void insert(int i,int value)//插入元素
    {
        //在heap尾部插入元素
        data[i] = value;
        count++;
        up(count);

    }
    int pop()//删除元素
    {
        int res = data[1];
        swap(data[1],data[count]);
        count--;
        down(1);
        return res;
    }
};