倍增
应用:进行递推时,若状态空间过大,则只推出2 k 2^k2k位置上的值。当需要其它位置上的值时,利用任意整数可以表示为若干个2的次幂项之和的性质从2 k 2^k2k位置的值中拼出结果。
例1 给定长度为N NN的数列a aa,然后在线询问若干次,每次给定一个整数T TT,求k m a x s . t . ∑ i = 1 k a i ⩽ T k_{max}\space s.t.\sum\limits_{i=1}^ka_i\leqslant Tkmax s.t.i=1∑kai⩽T.( 0 ⩽ T ⩽ ∑ i = 1 N a i ) (0\leqslant T\leqslant\sum\limits_{i=1}^Na_i)(0⩽T⩽i=1∑Nai)
思路1:二分查找
对{ a n } \{a_n\}{an}进行预处理求出前缀和S n S_nSn,然后二分{ S n } \{S_n\}{Sn}找k m a x s . t . S k ⩽ T k_{max}\space s.t.S_k\leqslant Tkmax s.t.Sk⩽T.
由于每次查找平均花费O ( l o g N ) O(logN)O(logN),当k kk较小时不如直接遍历。
思路2:倍增+二进制划分
先考虑这样一个问题:如何将一个未知的数n nn进行二进制分解?
若我们从低位开始分解,由于我们并不知道n nn的值,无法确认当前位上的是0还是1,所以无法进行分解。
当我们从高位开始分解时,若找到k 0 s . t . 2 k 0 > n k_0\space s.t.2^{k_0}>nk0 s.t.2k0>n,我们能确定∀ k ⩾ k 0 , 2 k ⩾ 2 k 0 > n \forall k\geqslant k_0,2^k\geqslant2^{k_0}>n∀k⩾k0,2k⩾2k0>n,即n nn的第k 0 k_0k0位及以上都不可能是1。
从k 0 k_0k0向下寻找到第一个k 1 s . t . 2 k 1 ⩽ n k_1\space s.t.2^{k_1}\leqslant nk1 s.t.2k1⩽n,我们能确定n nn的第k 1 k_1k1位一定是1。否则若k 1 k_1k1位不是1,那么n ⩽ ∑ k = 0 k 1 − 1 2 k = 2 k 1 − 1 < 2 k 1 ⩽ n ⇒ n < n n\leqslant \sum\limits_{k=0}^{k_1-1}2^k=2^{k_1}-1<2^{k_1}\leqslant n\Rightarrow n<nn⩽k=0∑k1−12k=2k1−1<2k1⩽n⇒n<n,矛盾!所以n nn的第k 1 k_1k1位是1。
从n nn中扣除2 k 1 2^{k_1}2k1后,问题转化为分解n − 2 k 1 n-2^{k_1}n−2k1,重复上述步骤即可将n nn完全分解。
所以我们要构造一种能使得从高位进行二进制分解的情形。
为此,我们分两个阶段来进行:
阶段1:倍增
依次考虑S 1 , S 1 + 2 1 , S 1 + 2 1 + 2 2 , … S_1,S_{1+2^1},S_{1+2^1+2^2},\dotsS1,S1+21,S1+21+22,…,直到出现S ∑ i = 0 k 0 2 i > T S_{\sum_{i=0}^{k_0}2^i}>TS∑i=0k02i>T停止。此时k m a x < ∑ i = 0 k 0 2 i k_{max}<\sum\limits_{i=0}^{k_0}2^ikmax<i=0∑k02i.令k = ∑ i = 0 k 0 − 1 2 i k=\sum\limits_{i=0}^{k_0-1}2^ik=i=0∑k0−12i,则k m a x − k < 2 k 0 k_{max}-k<2^{k_0}kmax−k<2k0,可对k m a x − k k_{max}-kkmax−k进行二进制划分。
阶段2:二进制划分
依次考虑S k + 2 k 0 − 1 , S k + 2 k 0 − 2 , … S_{k+2^{k_0-1}},S_{k+2^{k_0-2}},\dotsSk+2k0−1,Sk+2k0−2,…,若S k + 2 k 1 ⩽ T S_{k+2^{k_1}}\leqslant TSk+2k1⩽T,则相当于找到了k m a x − k k_{max}-kkmax−k的二进制最高位k 1 k_1k1;继续考虑S k + 2 k 1 + 2 k 1 − 1 , S k + 2 k 1 + 2 k 1 − 2 … S_{k+2^{k_1}+2^{k_1-1}},S_{k+2^{k_1}+2^{k_1-2}}\dotsSk+2k1+2k1−1,Sk+2k1+2k1−2…,相当于对k m a x − k − 2 k 1 k_{max}-k-2^{k_1}kmax−k−2k1继续进行二进制分解。当k m < 0 k_m<0km<0时,分解完毕,k m a x = k + ∑ i = 1 m − 1 2 k i k_{max}=k+\sum\limits_{i=1}^{m-1}2^{k_i}kmax=k+i=1∑m−12ki.
实现:
int p = 1, k = 0, sum = 0;
while (p) {
if (k + p <= N && sum + S[k + p] - S[k] <= T)
sum += S[k + p] - S[k], k += p, p <<= 1; // 1.
else p >>= 1;
}
细节:
1.数组a aa下标从1开始。S r − S l S_r-S_lSr−Sl所求的是( l , r ] (l,r](l,r]上的部分和,倍增过程即( 0 , 1 ] + ( 1 , 1 + 2 ] + ( 1 + 2 , 1 + 2 + 4 ] + ⋯ = ( 0 , 1 + 2 + 4 + ⋯ + 2 k 0 − 1 ] = [ 1 , k ] (0,1]+(1,1+2]+(1+2,1+2+4]+\dots=(0,1+2+4+\dots+2^{k_0-1}]=[1,k](0,1]+(1,1+2]+(1+2,1+2+4]+⋯=(0,1+2+4+⋯+2k0−1]=[1,k]
由于二进制划分过程中下标仍递增,所以两个阶段可以合并,如图:
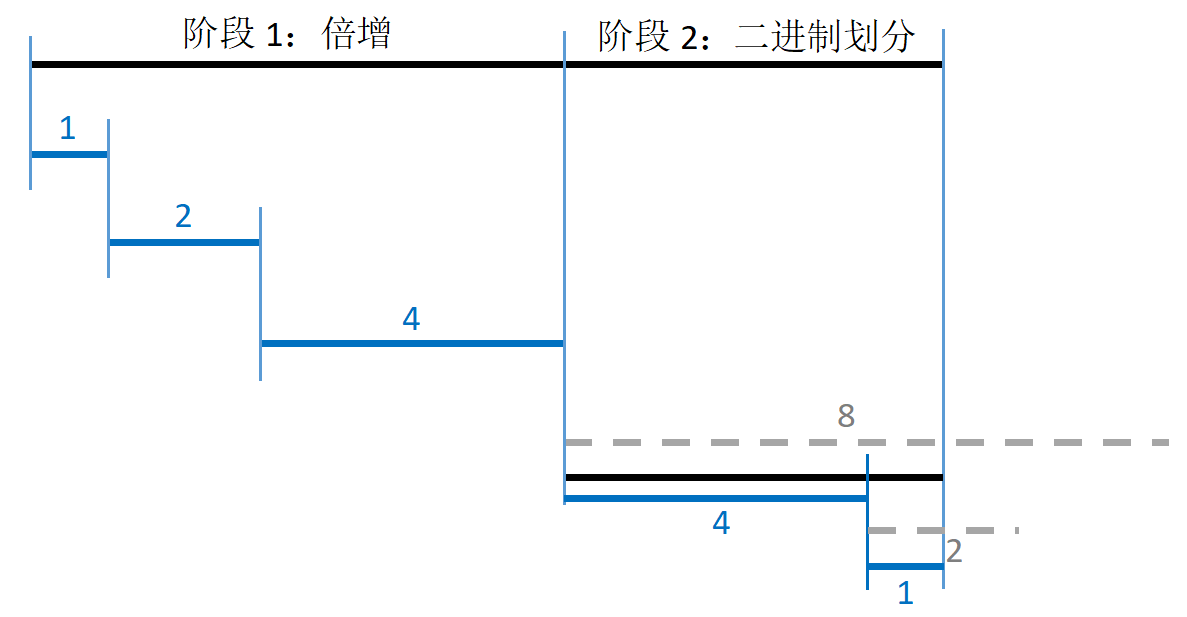
倍增与二分查找的比较:
倍增:利于已遍历状态空间的扩增(求增)
二分查找:利于有序状态空间的搜索(求全)
例2 Genius ACM
思路:倍增+二路归并
先解决校验值。当M = 1 M=1M=1时,显然S 校 验 = ( max S − min S ) 2 S_{校验}=(\max S-\min S)^2S校验=(maxS−minS)2.
当M = 2 M=2M=2时,参考M = 1 M=1M=1的情形将S SS进行排序。若所取的数S i S_iSi不为S 1 , S 2 , S n − 1 , S n S_1,S_2,S_{n-1},S_nS1,S2,Sn−1,Sn,那么∣ S i − S j ∣ < max ( ∣ S 1 − S j ∣ , ∣ S 2 − S j ∣ , ∣ S n − 1 − S j ∣ , ∣ S n − S j ∣ ) |S_i-S_j|<\max(|S_1-S_j|,|S_2-S_j|,|S_{n-1}-S_j|,|S_n-S_j|)∣Si−Sj∣<max(∣S1−Sj∣,∣S2−Sj∣,∣Sn−1−Sj∣,∣Sn−Sj∣).因此,我们只需考虑S 1 , S 2 , S n − 1 , S n S_1,S_2,S_{n-1},S_nS1,S2,Sn−1,Sn的组合方式即可。
又[ ( S n − S 1 ) 2 + ( S n − 1 − S 2 ) 2 ] − [ ( S n − S 2 ) 2 + ( S n − 1 − S 1 ) 2 ] = 2 S 1 S n − 1 + 2 S 2 S n [(S_n-S_1)^2+(S_{n-1}-S_2)^2]-[(S_n-S_2)^2+(S_{n-1}-S_1)^2]=2S_1S_{n-1}+2S_2S_n[(Sn−S1)2+(Sn−1−S2)2]−[(Sn−S2)2+(Sn−1−S1)2]=2S1Sn−1+2S2Sn− 2 S 1 S n − 2 S 2 S n − 1 = 2 S 2 ( S n − S n − 1 ) − 2 S 1 ( S n − S n − 1 ) = 2 ( S 2 − S 1 ) ( S n − S n − 1 ) > 0 -2S_1S_n-2S_2S_{n-1}=2S_2(S_n-S_{n-1})-2S_1(S_n-S_{n-1})=2(S_2-S_1)(S_n-S_{n-1})>0−2S1Sn−2S2Sn−1=2S2(Sn−Sn−1)−2S1(Sn−Sn−1)=2(S2−S1)(Sn−Sn−1)>0,所以S 1 S_1S1与S n S_nSn组合,S 2 S_2S2与S n − 1 S_{n-1}Sn−1组合。
类似的,当M > 2 M>2M>2时我们可以进行类似的组合。
所以从头尾选数进行组合即可求得S 校 验 S_{校验}S校验。
此处的S 校 验 S_{校验}S校验类似于上题的前缀和,我们可以采用相同的框架进行求解。
需要注意的一个细节是,求S 校 验 S_{校验}S校验时,我们需要对目标区间[ l , r ] [l,r][l,r]进行排序。这里会出现两个问题,一是每次进行排序时需花费O ( n l o g n ) O(nlogn)O(nlogn),加上O ( l o g n ) O(logn)O(logn)的倍增次数,算法复杂度为O ( n l o g 2 n ) O(nlog^2n)O(nlog2n);二是排序会对原数组造成影响,例如判断[ l , r + 2 k ] [l,r+2k][l,r+2k]时对[ l , r + 2 k ] [l,r+2k][l,r+2k]进行了排序,若此时不符合条件,区间回退至[ l , r + k ] [l,r+k][l,r+k],但[ l , r + k ] [l,r+k][l,r+k]中混入[ r + k + 1 , r + 2 k ] [r+k+1,r+2k][r+k+1,r+2k]的元素导致错误。
第一个问题可以采用二路归并实现:当排序区间从[ l , r ] → [ l , r + p ] [l,r]\rightarrow[l,r+p][l,r]→[l,r+p]时,可以对[ r + 1 , r + p ] [r+1,r+p][r+1,r+p]进行排序,再将[ l , r ] , [ r + 1 , r + p ] [l,r],[r+1,r+p][l,r],[r+1,r+p]进行归并,即可得到[ l , r + p ] [l,r+p][l,r+p]的有序区间。每次有效排序(即产生扩增时的排序)长度n i n_ini满足∑ n i = n \sum n_i=n∑ni=n,故∑ n i l o g n i < ∑ n i l o g n = n l o g n \sum n_ilogn_i<\sum n_ilogn=nlogn∑nilogni<∑nilogn=nlogn,复杂度降为O ( n l o g n ) O(nlogn)O(nlogn).
解决第二个问题需要三个数组:a [ ] , b [ ] , t e m p [ ] a[],b[],temp[]a[],b[],temp[],其中a [ ] a[]a[]存储原数据,t e m p [ ] temp[]temp[]为归并辅助数组,b [ ] b[]b[]为部分有序数组。三个数组工作如下:
扩增过程:[ l , r + p ] [l,r+p][l,r+p]符合条件,区间即从[ l , r ] [l,r][l,r]扩增到[ l , r + p ] [l,r+p][l,r+p].由于右端点只增不减,所以可以确定将有序的[ l , r + p ] [l,r+p][l,r+p]存入b [ ] b[]b[]不会导致后面元素的混入。
需要注意的是,我们不能仅将有序的[ r + 1 , r + p ] [r+1,r+p][r+1,r+p]直接放入b [ ] b[]b[]中,因为对[ l , r + p ] [l,r+p][l,r+p]整体排序后,[ l , r ] [l,r][l,r]部分也发生了改变,需将[ l , r + p ] [l,r+p][l,r+p]全部拷入。
试探过程:我们期望得到[ l , r + p 0 ] [l,r+p_0][l,r+p0]的有序序列,而这次扩增是在[ l , r ] [l,r][l,r]基础上的,所以b [ ] b[]b[]中[ l , r ] [l,r][l,r]部分是有序的。为了实现二路归并的效果,我们应该把a [ r + 1 , r + p 0 ] a[r+1,r+p_0]a[r+1,r+p0]拷入b [ ] b[]b[]中,并对b [ ] b[]b[]中该部分进行排序,再由归并后进入t e m p [ ] temp[]temp[]中。
此时t e m p [ ] temp[]temp[]中持有[ l , r + p 0 ] [l,r+p_0][l,r+p0]的有序序列,所以可以直接在t e m p [ ] temp[]temp[]中求取S 校 验 S_{校验}S校验.而传统的归并排序要求我们将t e m p [ ] temp[]temp[]拷入b [ ] b[]b[]中,但让未经确认的[ l , r + p 0 ] [l,r+p_0][l,r+p0]进入b [ ] b[]b[]会使得[ r + 1 , r + p 0 ] [r+1,r+p_0][r+1,r+p0]的元素混入[ l , r ] [l,r][l,r]中,从而产生未确定元素对已确定元素的破坏。
回到扩增过程,有序的[ l , r + p ] [l,r+p][l,r+p]的来源即是t e m p [ ] temp[]temp[],在试探过程中已经排好序放入t e m p [ ] temp[]temp[]中,可以在试探成功后直接取用。
实现:
int a[N], b[N], temp[N], m, n;
long long t;
bool check(int l, int mid, int r) {
if (r >= n)
return 0;
for (int i = mid + 1; i <= r; i++)
b[i] = a[i];
sort(b + mid + 1, b + r + 1); // STL区间左闭右开
int i = l, j = mid + 1; // 二路归并
for (int pos = l; pos <= r; pos++)
if (j > r || (i <= mid && b[i] < b[j]))
temp[pos] = b[i++];
else
temp[pos] = b[j++];
long long res = 0;
if (r - l + 1 <= 2 * m) // 数不够选
for (int i = 0; 2 * i < r - l; i++) // l + i < r - i
res += pow((temp[l + i] - temp[r - i]), 2);
else
for (int i = 0; i < m; i++)
res += pow((temp[l + i] - temp[r - i]), 2);
return res <= t;
}
int main() {
int k, p, ans, l, r;
cin >> k;
while (k--) {
cin >> n >> m >> t;
for (int i = 0; i < n; i++)
cin >> a[i];
ans = 0, l = 0, r = 0;
while (r < n) {
p = 1, b[r] = a[r]; // 1.
while (p) {
if (check(l, r, r + p)) {
r += p, p <<= 1;
for (int i = l; i <= r; i++)
b[i] = temp[i];
} else
p >>= 1;
}
ans++, l = ++r; // 1.
}
cout << ans << endl;
}
return 0;
}
细节:
1.当产生新的分段时,[ l 1 , r 1 ] [l_1,r_1][l1,r1]划分结束,l 2 = r 1 + 1 , r 2 = l 2 l_2=r_1+1,r_2=l_2l2=r1+1,r2=l2开始新的划分,但在试探过程中,我么假定了[ l , r ] [l,r][l,r]是有序序列,而有序序列应被拷入b [ ] b[]b[]中,所以每一次开始新的分段时,需将a [ l ] ( a [ r ] ) a[l](a[r])a[l](a[r])拷入b [ ] b[]b[]中以保证正确性。
ST算法
应用:求解RMQ问题
RMQ问题:给定长度为N NN的数列a aa,在线回答数组a aa中下标在l ∼ r l\sim rl∼r之间的数的最大值为多少
思路:倍增
根据倍增思想,我们希望引入成倍增长的量,易见区间长度是很好的选择。为了描述各个区间,规定长度后还需规定起点,所以我们将起点和长度作为状态描述的参量。
定义状态F [ i ] [ j ] ≜ max i ⩽ k ⩽ i + 2 j − 1 a k F[i][j]\triangleq \max\limits_{i\leqslant k\leqslant i+2^j-1}a_kF[i][j]≜i⩽k⩽i+2j−1maxak,即从a i a_iai开始区间长度为2 j 2^j2j(i + 2 j − 1 − i + 1 = 2 j i+2^j-1-i+1=2^ji+2j−1−i+1=2j)的区间的最大值。边界为F [ i ] [ 0 ] = a i F[i][0]=a_iF[i][0]=ai.
接着考虑状态转移,考虑到最大值的性质:两个区间合起来的最大值等于两个区间各自的最大值的最大值,所以F [ i ] [ j ] = max { F [ i ] [ j − 1 ] , F [ i + 2 j − 1 ] [ j − 1 ] } F[i][j]=\max\{F[i][j-1],F[i+2^{j-1}][j-1]\}F[i][j]=max{F[i][j−1],F[i+2j−1][j−1]}(前半个区间到i + 2 j − 1 − 1 i+2^{j-1}-1i+2j−1−1,后半个区间从i + 2 j − 1 i+2^{j-1}i+2j−1开始)
状态空间大小为n ∗ l o g n n*lognn∗logn,故预处理F [ n ] [ l o g n ] F[n][logn]F[n][logn]的时间复杂度为O ( n l o g n ) O(nlogn)O(nlogn).
接着考虑查询过程。由于两个区间合起来的最大值等于两个区间各自的最大值的最大值,所以我们可以将待查区间分为两段(重合不影响合区间,只需要求两段区间的合将待查询区间覆盖即可)。结合我们定义的状态,我们可以考虑使用F [ l ] [ k ] F[l][k]F[l][k]和F [ r − 2 k + 1 ] [ k ] F[r-2^k+1][k]F[r−2k+1][k]进行查询,如图:
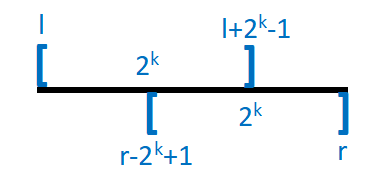
故要求{ 2 k ⩽ l − r + 1 , 2 ⋅ 2 k ⩾ l − r + 1 \left\{\begin{array}{ll}2^k\leqslant l-r+1, \\2\cdot2^k\geqslant l-r+1\end{array}\right.{2k⩽l−r+1,2⋅2k⩾l−r+1取k = ⌊ l o g 2 ( l − r + 1 ) ⌋ k=\lfloor log_2(l-r+1)\rfloork=⌊log2(l−r+1)⌋即可(p − 1 ⩽ p − 1 < ⌊ p ⌋ ⩽ p p-1\leqslant p-1<\lfloor p\rfloor\leqslant pp−1⩽p−1<⌊p⌋⩽p)。
实现:
for (int i = 1; i <= n; i++) f[i][0] = a[i];
int t = log[n]; // 1.
for (int j = 1; j <= t; j++)
for (int i = 1; i <= n - (1 << j) + 1; i++) // 2.
f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
void query(int l, int r) {
int k = log[r - l + 1];
return max(f[l][k], f[r - (1 << k) + 1][k]);
}
细节:
1.此处使用预处理的l o g loglog表计算l o g 2 n log_2nlog2n,预处理l o g loglog表实现如下:
for (int i = 0; i <= n; i++)
for (int j = 1 << i; j < 1 << (i + 1); j++) log[j] = i;
即∀ n ∈ [ 2 i , 2 i + 1 ) , n ∈ N ∗ , ⌊ l o g 2 n ⌋ = i \forall n\in[2^{i},2^{i+1}),n\in\N^*,\lfloor log_2n\rfloor=i∀n∈[2i,2i+1),n∈N∗,⌊log2n⌋=i.
或者可以使用c m a t h cmathcmath库的l o g loglog函数,该函数以10为底。由换底公式知,l o g 2 n = l g n l g 2 log_2n=\dfrac{lgn}{lg2}log2n=lg2lgn,故l o g [ n ] = l o g ( n ) / l o g ( 2 ) log[n]=log(n)/log(2)log[n]=log(n)/log(2)
2.状转方程右边的j − 1 j-1j−1小于左边的j jj,所以需要按照j jj递增的顺序进行枚举,故将j jj放在外层循环;递推i ii时需判断边界:F [ i ] [ j ] F[i][j]F[i][j]本身含义是[ i , i + 2 j − 1 ] [i,i+2^j-1][i,i+2j−1],故i + 2 j − 1 ⩽ n ⇔ i ⩽ n − 2 j + 1 i+2^j-1\leqslant n\Leftrightarrow i\leqslant n-2^j+1i+2j−1⩽n⇔i⩽n−2j+1