6 高级排序算法
6.1 归并排序
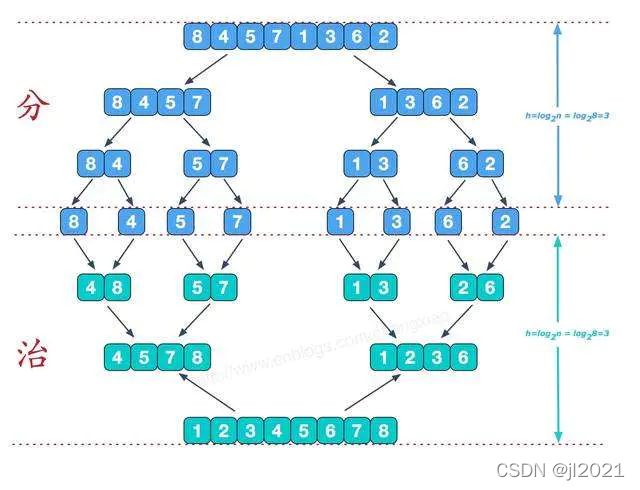
6.1.1 步骤
- 实现两个有序数组的合并
void Merge(int* arr,int n,int mid)
- 拆分并合并数组
void MergeSort(int* arr,int n)
6.1.2 代码
- 递归实现归并排序
void Merge(int* arr,int n,int mid){
int temp[n];
memcpy(temp,arr,n*sizeof(int));
int p = 0,q = mid,k = 0;
while(p < mid && q < n){
arr[k++] = temp[p] < temp[q]? temp[p++]:temp[q++];
}
if(p < mid) memcpy(arr+k,temp+p,(mid-p)*sizeof(int));
if(q < n) memcpy(arr+k,temp+q,(n-q)*sizeof(int));
}
void MergeSort(int* arr,int n){
if(n <= 1) return;
int mid = n/2;
MergeSort(arr,mid);
MergeSort(arr+mid,n-mid);
Merge(arr,n,mid);
}
- 迭代实现归并排序
void Merge(int* arr,int n,int mid){
int temp[n];
memcpy(temp,arr,n*sizeof(int));
int p = 0,q = mid,k = 0;
while(p < mid && q < n){
arr[k++] = temp[p] < temp[q]? temp[p++]:temp[q++];
}
if(p < mid) memcpy(arr+k,temp+p,(mid-p)*sizeof(int));
if(q < n) memcpy(arr+k,temp+q,(n-q)*sizeof(int));
}
int min(int a,int b){
return a < b?a:b;
}
void SubMerge(int* arr,int n,int step){
int len = n;
for(int i = 0;i+step<n;i+=step*2){
Merge(arr+i,min(2*step,len),min(step,len));
len -= 2*step;
}
}
void MergeSort(int* arr,int n){
for(int i = 1;i < n;i *= 2){
SubMerge(arr,n,i);
}
}
6.1.3 复杂度
时间复杂度
一共拆分log2n次,每次比较n个元素,一共比较nlog2n次。空间复杂度
随着n的增长,排序需要增加额外空间n+log2n(临时数组n和递归调用函数栈log2n),空间复杂度为O(n)。
6.2 快速排序
6.2.1 原理
左游标是i哨兵,右游标是j哨兵
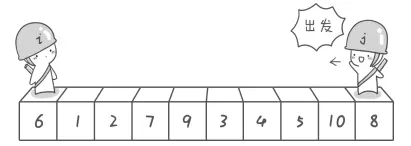
第一次交换
以6为基准,哨兵j从右向左找到第一个小于基准数6的值,哨兵i从左向右找到第一个大于基准数6的值(一定是哨兵j先动)
为什么右边哨兵先动?
如果选取最左边的数arr[left]作为基准数,那么先从右边开始可保证i,j在相遇时,相遇数是小于基准数的,交换之后temp所在位置的左边都小于temp。
但如果先从左边开始,相遇数是大于基准数的,无法满足temp左边的数都小于它。所以进行扫描,要从基准数的对面开始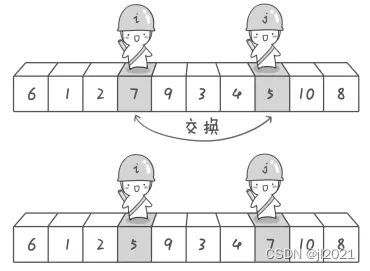
哨兵j发现7>6,哨兵i发现5<6,然后进行值交换。
第二次交换
哨兵j继续向左移动,哨兵j继续向右移动。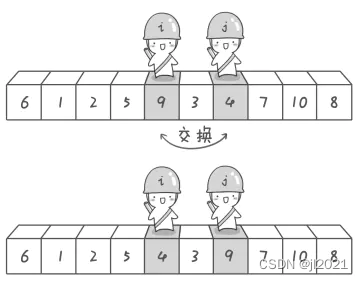
4<6,9>6。进行第二次交换。基准交换
哨兵在值为3处相遇,因此3和6进行交换。至此第一轮探测结果,6已归位。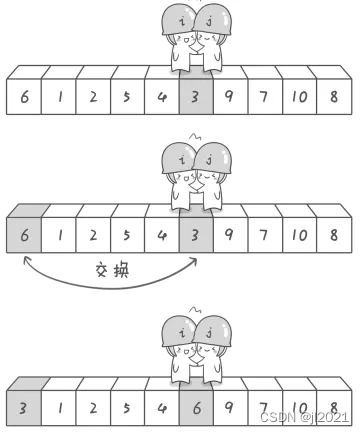
依次进行第二轮第三轮探测与交换。整个过程简化如下: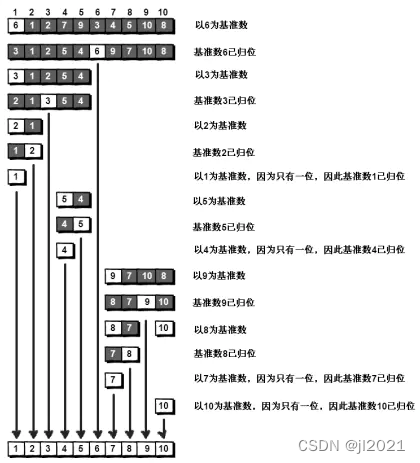
6.2.2 步骤
- 根据基准元素重排数组
int partition(int* arr,int n)
- 依次排列两个部分
void QuickSort(int* arr,int n)
6.2.3 参考代码
实例:
int partition(int* arr,int n){
int key = arr[0];
int i = 0,j = n-1;
while(i < j){
while(arr[j] >= key && i < j){
--j;
}
if(i >= j) break;
while(arr[i] <= key && i < j){
++i;
}
if(i >= j) break;
swap(arr+i,arr+j);
}
swap(arr,arr+i);
return i;
}
void QuickSort(int* arr,int n){
if(n <= 1) return;
int index = partition(arr,n);
QuickSort(arr,index);
QuickSort(arr+index+1,n-1-index);
}
6.2.4 时间复杂度
一共拆分log2n次,每次比较n个元素,一共比较nlog2n次。
6.2.5 空间复杂度
随着n的增长,排序需要增加额外空间log2n(递归函数栈空间),空间复杂度为O(log2n)。
6.3 希尔排序
6.3.1 原理
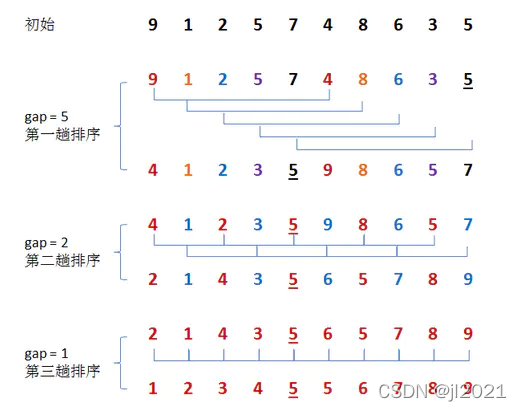
1、给定一个长度n的列表,选择一定的步长step,将列表分成若干个子列表sublist。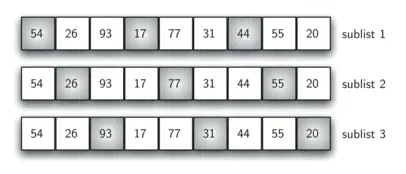
例如:长度n=9步长step=3分成3个子列表sublist。
2、对每一个子列表sublist进行插入排序。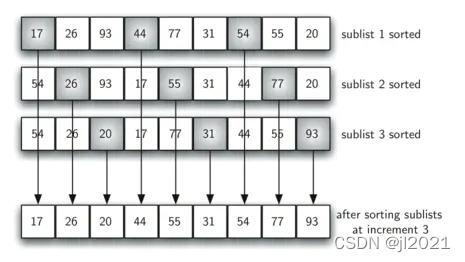
3、依次减小步长step,重复上述操作。直到step为1。
- 希尔排序比插入排序的优势:
通过分组排序使元素逐渐靠近最终位置,从而减少了插入排序 时的移动次数。(先粗调再微调)
6.3.2 步骤
- 1、划分间距step并执行排序
void ShellSort(int* arr,int n)
- 2、根据间距
step执行插入排序
void insertsort(int* arr,int n,int step)
- 3、根据间距
step插入
void insert(int* arr,int n,int step)
6.3.4 代码
void insert(int* arr,int n,int step){
for(int i = n-1-step;i >= 0;i -= step){
if(arr[i] > arr[i+step]){
swap(arr+i+step,arr+i);
}else{
break;
}
}
}
void insertsort(int* arr,int n,int step){
for(int i = 0;i <= n;++i){
insert(arr,i,step);
}
}
void ShellSort(int* arr,int n){
if(n <= 1) return;
for(int i = n/2;i > 0;i /= 2){
insertsort(arr,n,i);
}
}
与插入排序对比:
6.4 小结
| 算法 | 时间复杂度 | 空间复杂度 | 是否稳定? |
|---|---|---|---|
| 快速排序 | 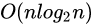 | 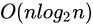 | 否 |
| 归并排序 | 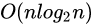 | 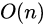 | 是 |
| 希尔排序 | 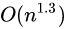 | 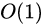 | 否 |
6.5 算法选择标准
| 准则 | 排序算法 |
|---|---|
| 很少的元素 | 插入排序 |
| 几乎有序的元素 | 插入排序 |
| 关注最坏的情况 | 堆排序 |
| 希望能够得到一个好的平均情况下性能 | 快速排序 |
| 元素是从一个密集集合中抽取出 | 桶排序 |
| 希望尽可能少的写代码 | 插入排序 |
6.6 排序算法代码汇总
#include <iostream>
#include <vector>
#include <string.h>
using namespace std;
void PrintArr(int* arr,int n){
for(int i = 0;i < n;++i){
cout << arr[i] << " ";
}
cout << endl;
}
void swap(int* a,int* b){
int c = *b;
*b = *a;
*a = c;
}
void BubbleSort(int* arr,int n){
for(int i = 0;i < n;++i){
for(int j = i+1;j < n;++j){
if(arr[i] > arr[j]){
swap(arr+i,arr+j);
}
}
}
}
void SelectSort(int* arr,int n){
for(int i = 0;i < n;++i){
int index = 0;
for(int j = 1;j < n-i;++j){
if(arr[j] > arr[index]){
index = j;
}
}
swap(arr+n-1-i,arr+index);
}
}
void InsertSort(int* arr,int n){
for(int i = 2;i < n+1;++i){ //i表示元素个数
for(int j = 0;j < i-1;++j){
int last = arr[i-1];
if(arr[j]>last){
memmove(arr+j+1,arr+j,sizeof(int)*(i-1-j));
arr[j] = last;
break;
}
}
}
}
void Merge(int* arr,int n,int mid){
int temp[n];
memcpy(temp,arr,sizeof(int)*n);
int p = 0,q = mid,k = 0;
while(p < mid && q < n){
arr[k++] = temp[p] < temp[q]? temp[p++]:temp[q++];
}
if(p < mid) memcpy(arr+k,temp+p,sizeof(int)*(mid-p));
if(q < n) memcpy(arr+k,temp+q,sizeof(int)*(n-q));
}
void MergeSort(int* arr,int n){
if(n <= 1) return;
int mid = n/2;
MergeSort(arr,mid); //mid表示传入数组长度
MergeSort(arr+mid,n-mid);
Merge(arr,n,mid);
}
int Partition(int* arr,int n){
int key = arr[0];
int i = 0,j = n-1;
while(i < j){
while(arr[j] >= key && i < j){
--j;
}
if(i >= j) break;
while(arr[i] <= key && i < j){
++i;
}
if(i >= j) break;
swap(arr+i,arr+j);
}
swap(arr,arr+i);
return i;
}
void QuickSort(int* arr,int n){
if(n <= 1) return;
int index = Partition(arr,n);
QuickSort(arr,index); //index表示传入数组长度
QuickSort(arr+index+1,n-1-index); //arr+index元素已归位,所以从arr+index+1开始
}
void insert(int* arr,int n,int step){
for(int i = n-1-step;i >= 0;i -= step){
if(arr[i] > arr[i+step]){
swap(arr+i,arr+i+step);
}else{
break;
}
}
}
void insertsort(int* arr,int n,int step){
for(int i = 0;i <= n;++i){
insert(arr,i,step);
}
}
void ShellSort(int* arr,int n){
for(int i = n/2;i > 0;i/=2){
insertsort(arr,n,i);
}
}
int main(){
int arr[6] = {1,3,6,4,2,7};
int len = sizeof(arr)/sizeof(int);
PrintArr(arr,len);
//BubbleSort(arr,len);
//SelectSort(arr,len);
//InsertSort(arr,len);
//MergeSort(arr,len);
//QuickSort(arr,len);
ShellSort(arr,len);
PrintArr(arr,len);
}
版权声明:本文为qq_42488216原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。