哈希查找法
哈希法(或称散列法)这个主题通常和查找法一起讨论,主要原因是哈希法不仅用于数据的查找,在数据结构的领域中,还能将它应用在数据的建立、查找、删除与更新中
例如符号表在计算机上的应用领域很广泛,包含汇编程序、编译程序、数据库使用的数据字典等,都是利用提供的名称来找到对应的属性。符号表按其特性可以分为两类:静态表(Static Table)和动态表(Dynamic Table)。而“哈希表”则是属于静态表中的一种,是将相关的数据和键值存储在一个固定大小的表格中
哈希法简介
基本上,哈希法就是将本身的键值通过特定的数学函数运算或者使用其他的方法转换成相对应的数据存储地址。哈希法使用的数学函数就称为“哈希函数”.
bucket:(桶),哈希表中存储数据的位置,每一个位置对应唯一的一个地址(bucket address)。桶就好比一个记录
slot:(槽),每一个记录中可能包含好几个字段,而slot指的就是"桶"中的字段
collision:(碰撞),如果两项不同的数据经过哈希函数运算后对应到相同的地址,就称为碰撞
溢出:如果数据经过哈希函数运算后所对应到的bucket已满,就会使bucket发生溢出
哈希表:存储记录的连续内存。哈希表是一种类似数据表的索引表格,其中可分为n个bucket,每个bucket又可以分作m个slot
索引 姓名 电话 001 Allen 7726 002 Jack 7727 003 May 7728 同义词:(Synonym),当两个标识符I1和I2经过哈希函数运算后所得的数值相同时,即f(i1)=f(i2),称I1和I2对于f这个哈希函数是同义词
加载密度:(Loading Factor),所谓加载密度,是指标识符的使用数目除以哈希表内槽的总数
α(加载密度) = n(标识符的使用数目) / s(每一个桶内的槽数) * b(桶的数目)
完美哈希:(Perfect Hashing),指没有碰撞也没有溢出的哈希函数
通常在设计哈希函数时应该遵循以下几个原则
- 降低碰撞和溢出的产生
- 哈希函数不宜过于复杂,越容易计算越佳
- 尽量把文字的键值转换为数字的键值,以利于哈希函数的运算
- 所设计的哈希函数计算得到的值尽量能均匀地分布在每一个桶中,不要太过于集中在某些桶内,这样就可以降低碰撞,并减少溢出的处理
常见的哈希函数
常见的哈希法有除留余数法、平方取中法、折叠法和数字分析法
除留余数法
最简单的哈希函数是将数据除以某一个常数后,去余数来当索引。例如在一个有13个位置的数组中,只使用了7个地址,值分别是12,65,70,99,33,67,48。我们卡伊把数组内的值除以13,并以其余数来当数组的下标(即作为索引),可以用以下这个式子来表示:
h(key) = key mod B
在这个例子中,我们所使用的B = 13,一般而言,建议选择的B最好是质数,以上建立的哈希表如下所示:
| 索引 | 数据 |
|---|---|
| 0 | 65 |
| 1 | |
| 2 | 67 |
| 3 | |
| 4 | |
| 5 | 70 |
| 6 | |
| 7 | 33 |
| 8 | 99 |
| 9 | 48 |
| 10 | |
| 11 | |
| 12 | 12 |
平方取中法
平方取中法和除留余数法相当类似,就是先计算数据的平方,之后再取中间的某段数字作为索引。
将12,65,70,99,33,67,51平方之后
144,4225,4900,9801,1089,4489,2601
再去百位数和十位数作为键值,分别为
14,22,90,80,08,48,60
折叠法
折叠法就是将数据转换为一串数字之后,现将这串数字折成几个部分,再把他们相加起来,就可以计算出这个键值的Bucket Address,例如一个数据,转换成数字后为2365479125443,若每4个数字为一个部分,则可以拆成2365,4791,2544,3.将这4组数字加起来后即是索引值
2365 + 4791 + 2544 + 3 = 9703
此时的9703就是桶地址
在折叠法中有两种做法,如上例直接将每一部分相加所得的值作为其桶地址,这种做法称为“移动折叠法”。但哈希法的设计原则之一就是降低碰撞,如果希望降低碰撞的机会,就可以将上述每一部分的数字中的奇数或者偶数反转,再相加来取得其桶地址,这种改进式的做法称为“边界折叠法”(folding at the boundaries)
将偶数反转
2365
1974
2544
3
6886----------------> 桶地址
将奇数反转
5632
4791
4452
3
14878-------------->桶地址
数字分析法
数字分析法适合于数据不会更改,且为数字类型的静态表。在决定哈希函数时先逐一检查数据的相对位置和分布情况,将重复性高的部分删除。
看完上面几种哈希函数之后,其实也可以发现哈希函数并没有一定的规则可寻,可能使用其中某一种方法,也可能同时使用好几种方法,所以哈希常常被用来处理数据的加密和压缩。但是,哈希法常会遇到“碰撞”和“溢出”的情况。
碰撞和溢出问题的处理
没有一种哈希函数能够确保数据经过哈希运算处理后所得到的索引值都是唯一的,当索引值重复时,就会产生碰撞的问题,而碰撞的情况在数据量大的时候特别容易法还是能。因此,如何在碰撞后处理溢出的问题就显得相当重要
线性探测法
线性探测法是当发生碰撞情况时,若该索引对应的存储位置已经有数据,则以线性的方式往后寻找空的存储位置,,一旦找到位置就把数据放进去。线性探测法通常把哈希的位置视为环形结构,如此一来,当后面位置已经被填满而前面还有位置是,可以将数据放到前面
python的线性探测算法如下:
def createTable(num,index): #建立哈希表子程序
tmp = num % INDEXBOX
while True:
if index[tmp] == -1:
index[tmp] = num
break
else:
tmp = (tmp + 1) % INDEXBOX #否则往后寻找位置存放
设计python程序,以除留余数法的哈希函数取得索引值,再以线性探测法来存储数据
import random
INDEXBOX = 10 #哈希表最大元素
MAXNUM = 7 #最大数据个数
#打印数据子程序
def printData(data,max_number):
print('\t',end='')
for i in range(max_number):
print('[%2d] '%data[i],end='')
print()
#创建哈希表子程序
def createTable(num,index): #建立哈希表子程序
tmp = num % INDEXBOX
while True:
if index[tmp] == -1:
index[tmp] = num
break
else:
tmp = (tmp + 1) % INDEXBOX #否则往后寻找位置存放
#主程序
def main():
index = [None] * INDEXBOX
data = [None] * MAXNUM
print('原始数据值:')
for i in range(MAXNUM):
data[i] = random.randint(1,20)
for i in range(INDEXBOX): #清除哈希表
index[i] = -1
printData(data,MAXNUM)
print("哈希表的内容:")
for i in range(MAXNUM): #建立海西表
createTable(data[i],index)
print(' %2d =>'%data[i],end='') #打印单个元素的哈希表位置
printData(index,INDEXBOX)
print('完成的哈希表:')
printData(index,INDEXBOX)
if __name__ == '__main__':
main()

平方探测法
线性探测法有一个缺点,就是相类似的键值经常会聚集在一起,因此可以考虑以平方探测法来加以改进。在平方探测法中,当溢出发生时,下一次查找的地址就是(f(x)+12)modB与(f(x)-i2)modB,即让数据值加或者减去i的平方
再哈希法
再哈希就是一开始先设置一系列的哈希函数,如果使用第一种哈希函数出现溢出,就改用第二种,如果第二种也出现溢出,就改用第三种,一直到没有发生溢出为止。
链表法
将哈希表的所有空间建立n个链表,最初的默认值只有n个链表头。如果发生溢出,就把相同地址的键值连接在链表头的垢面,就形成一个键表,直到所有的可用空间全部用完为止
python的再哈希算法如下
def createTable(val): #建立哈希表子程序
global indextable
newnode = Node(val)
myhash = val % 7 #哈希函数除以7取余数
current = indextable[myhash]
if current.next == None:
indextable[myhash].next = newnode
else:
while current.next != None:
current = current.next
current.next = newnode #将节点加入链表
设计一个python程序,使用链表来进行再哈希处理
import random
INDEXBOX = 7 #哈希表元素个数
MAXNUM = 13 #数据个数
class Node: #声明链表结构
def __init__(self,val):
self.val = val
self.next = None
global indextable
indextable = [Node] * INDEXBOX
#建立哈希表子程序
def createTable(val): #建立哈希表子程序
global indextable
newnode = Node(val)
myhash = val % 7 #哈希函数除以7取余数
current = indextable[myhash]
if current.next == None:
indextable[myhash].next = newnode
else:
while current.next != None:
current = current.next
current.next = newnode #将节点加入链表
#打印哈希表子程序
def printData(val):
global indextable
pos = 0
head = indextable[val].next #起始指针
print(' %2d:\t'%val,end='') #索引地址
while head != None:
print('[%2d]-'%head.val,end='')
pos += 1
if pos % 8 == 7:
print('\t')
head = head.next
print()
#主程序
def main():
data = [0] * MAXNUM
index = [0] * INDEXBOX
for i in range(INDEXBOX): #清除哈希表
indextable[i] = Node(-1)
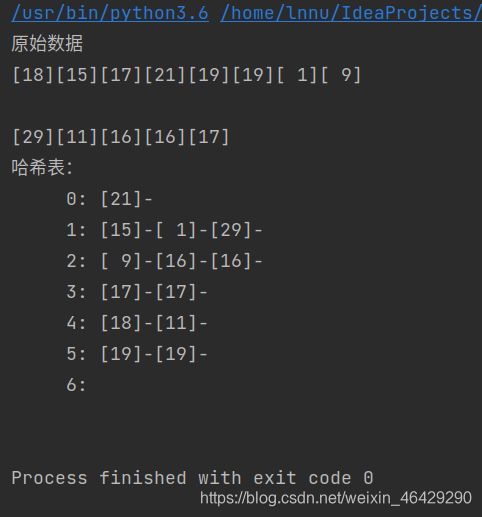
print('原始数据')
for i in range(MAXNUM):
data[i] = random.randint(1,30) #随机建立原始数据
print('[%2d]'%data[i],end='')
if i % 8 == 7:
print('\n')
print('\n哈希表:')
for i in range(MAXNUM):
createTable(data[i]) #建立哈希表
for i in range(INDEXBOX):
printData(i) #打印哈希表
print()
if __name__ == '__main__':
main()