——笔记整理自中国大学mooc
偏度(Skewness)系数
引例:
1952年马科维茨把组合投资收益和风险定义为均值和方差(标准差)。
但均值和方差一定时, 偏斜程度有别。

偏度系数的计算
(一)基于算术平均数与众数或中位数
皮尔逊偏度系数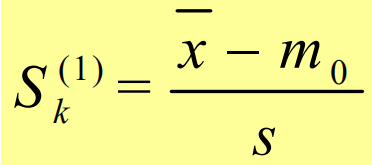

变动范围(-3,3)
(二)利用四分位数求偏度系数
鲍莱偏度系数


(三)利用动差(矩)法求偏度系数
t阶动差(矩)是这个数据里面的所有数据减去一个常数a的t次方,然后算一个平均。
求峰度和偏度,离散的对标用的都是算数平均数。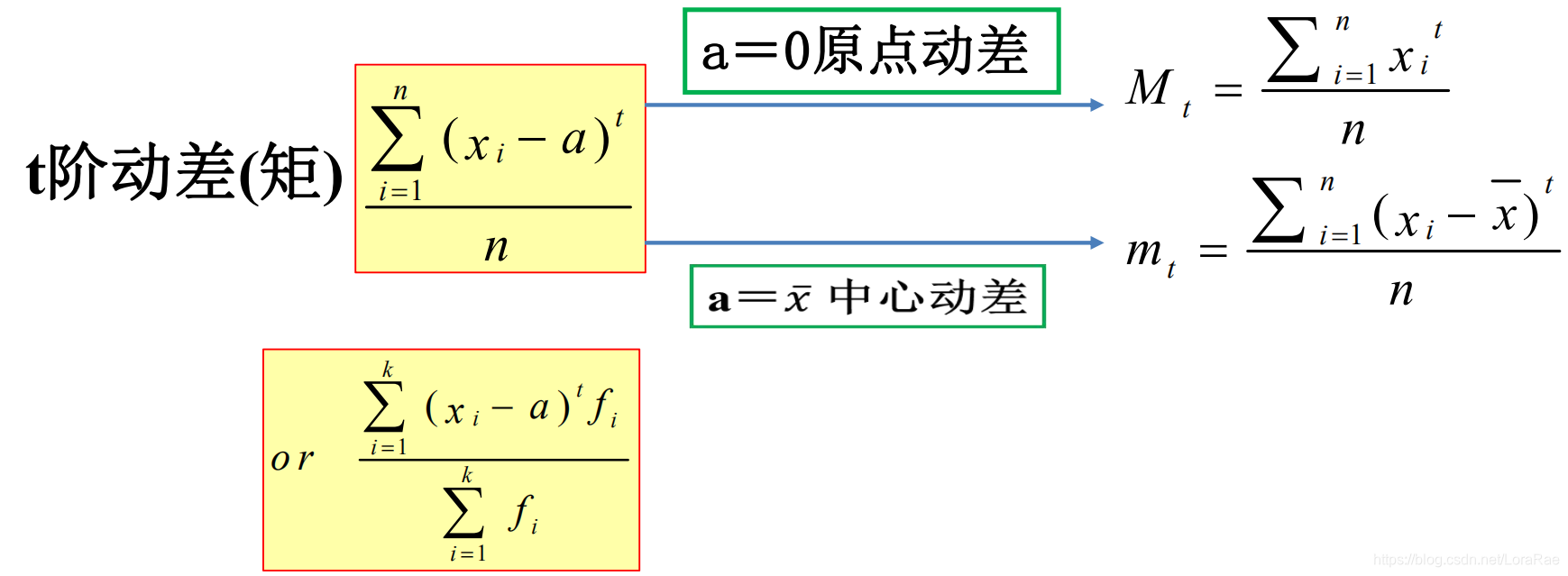


峰度(Kurtosis)系数
主要反映分布的陡峭性。
计算方法

例子
动差法求偏度系数和峰度系数:


版权声明:本文为LoraRae原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。