过程

给：minf(x)，初始点：x0
过程①
求出下降方向d：∇^2 f(x0) * d =- ∇f(x0)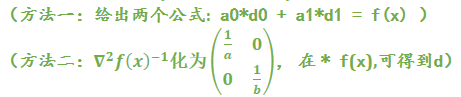

过程②
更新x：x1 = x0 + d
过程③
||∇f(x)|| < ε,则得到x* = x

代码

import matplotlib.pyplot as plt
import sympy
import numpy as np
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False
x1 = sympy.Symbol('x1')
x2 = sympy.Symbol('x2')
f = x1 ** 2 + x2 ** 2 + x1 * x2 + 2 * x1 - 3 * x2
# 梯度向量 gfun
gfun = lambda x: np.array([2 * x[0] + x[1] + 2 , 2 * x[1] + x[0] - 3])

# 海森矩阵 hess
hess =lambda x: np.array([[2 , 1], [ 1 , 2]])
x = np.array([0.0,0.0])
def newton(x):
    lx1=[]
    lx2=[]
    for i in range(100):
        lx1.append(x[0])
        lx2.append(x[1])
        dk = gfun(x)
        print(x)
        length = np.linalg.norm(dk)
        # print(length)
        if length < 0.05:
            print(x)
            break
        else:
            v2fk = hess(x)
            dk = -1*np.linalg.solve(v2fk, dk)
            x += dk
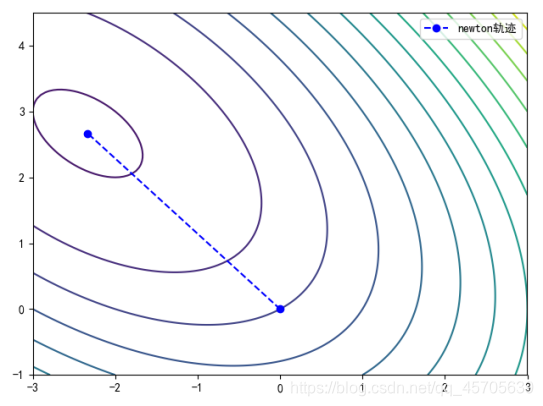
    plt.plot(lx1,lx2,linestyle="--", marker="o", color="blue",label="newton轨迹")

def Graph():
    X1 = np.arange(-3, 3 + 0.05, 0.05)
    X2 = np.arange(-1, 4.5 + 0.05, 0.05)
    [x1, x2] = np.meshgrid(X1, X2)
    f = x1 ** 2 + x2 ** 2 + x1 * x2 + 2 * x1 - 3 * x2  # 给定的函数
    plt.contour(x1, x2, f, 15)

Graph()
newton(x)
plt.legend()
plt.show()
#ipp pcp